Цели:
- ввести понятие правильной пирамиды;
- научить изображать правильную пирамиду;
- познакомить со свойствами ее элементов;
- получить вывод формулы площади боковой поверхности;
- развивать интуицию, пространственное воображение.
Ход урока
- Проверка домашнего задания
- Повторяем определение пирамиды, ее элементов, решаем устно задачи:
- Основание пирамиды прямоугольник, одно боковое ребро перпендикулярно основанию пирамиды. Определите вид боковых граней. Выполните чертеж “рис.1”.
- Используя “рис.1” решите задачу: S ABCD –
пирамида, ABCD – квадрат, АВ = 2см,
№ 243 Основание пирамиды DABS является ![]() АВС, у которого АВ = АС = 13 см, ребро AD
перпендикулярно плоскости основания и равно 9 см.
Найдите площадь боковой поверхности пирамиды.,
АВС, у которого АВ = АС = 13 см, ребро AD
перпендикулярно плоскости основания и равно 9 см.
Найдите площадь боковой поверхности пирамиды.,
№ 244 Основание пирамиды DABS является прямоугольный треугольник АВС, у которого гипотенуза АВ равна 29 см, катет АС = 21см. Ребро DA перпендикулярно плоскости основания и равно 20 см. Найдите площадь боковой поверхности пирамиды.
Решения записаны на доске, выделяем главные этапы решений.
![]() SAB = 600
Найдите боковую поверхность пирамиды.
SAB = 600
Найдите боковую поверхность пирамиды.
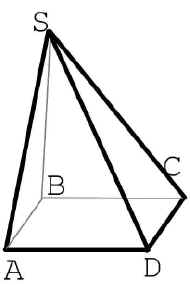
III. Объяснение нового материала.
- Сформулируйте определение правильной пирамиды.
- По “рис.2”, устно доказываем, что в правильной пирамиде:
(Учащиеся могут составить его сами аналогично определению правильной призмы, при этом выясняем, является ли пирамида задачи 2 правильной).
После обсуждения этого вопроса, составляем полное определение правильной пирамиды, учимся ее рисовать (“рис.2”), водим понятие апофемы (ha).
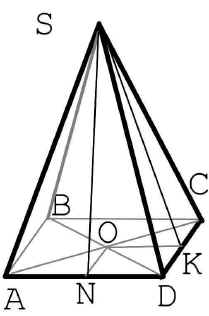
- боковые ребра равны;
- боковые грани – равнобедренные треугольники;
- боковые грани равны;
- апофемы раны;
- двугранные углы при основании равны.
После этого каждый ученик, согласно своему варианту, записывает одно из доказательств, затем проверка и корректировка в парах, и пятеро учащихся по выбору учителя зачитывают свои записи.
По окончании этой работы следующие вопросы:
- Расскажите, как найти боковую поверхность правильной пирамиды?
- Докажите, что Sбок = Ѕ Росн х hа
3. Самостоятельно в тетрадях оформляется доказательство теоремы о боковой поверхности правильной пирамиды, тем, кто не может это сделать самостоятельно, разрешается воспользоваться учебником стр.67.
Самое удачное, четко сформулированное доказательство один из учащихся записывает на доске.
IV. Решение задач
№254 (а) В правильной треугольной пирамиде сторона основания равна а, высота равна Н. Найдите боковое ребро пирамиды.
Устно разбираем два способа решения задачи, используя:
- свойство медиан;
- понятие радиуса описанной окружности.
Оформляем в тетрадях по вариантам, проверка в парах и два ученика оформляют задачи на доске.
Пока идет оформление задач на доске, устно обсуждаем два способа решения задачи.
№ 257 Высота правильной треугольной пирамиды равна h, а двугранный угол при стороне основания равен 450. найдите площадь поверхности пирамиды.
При решении этой задачи также используем свойство медиан и понятие радиуса вписанной окружности. Решение и оформление аналогично предыдущей.
V. Итог урока.
Контрольные вопросы по изученной теме.
Домашнее задание № 254 (в) 258
Урок 2.
Урок посвящен решению задач. Класс делится на группы по 4 человека (разноуровневые). Группам предлагаются одинаковые задания. Работа организуется по “методу пилы” (“Новые педагогические и информационные технологии в системе образования” под ред. д-ра. пед. наук проф. Е.С.Полот.М., изд. “Академия”, 2002). Каждый ученик в группе выполняет свое задание. Кроме консультаций с учителем, может осуществлять консультации с “экспертами” по этому вопросу из других групп. Затем идет общее обсуждение каждой задачи в группе, так чтобы любой ученик мог решить любую из задач. Когда группы готовы, учитель может вызвать любого ученика из каждой группы для объяснения решения задачи.
Задача № 1
Боковое ребро правильной треугольной пирамиды равно 5 см., а высота – 3 см. Найдите площадь полной поверхности.
Задача № 2
Апофема правильной шестиугольной пирамиды равна 5 см, а высота – 4 см. Найдите площадь боковой поверхности.
Задача № 3.
В правильной треугольной пирамиде боковые
грани наклонены к основанию под углом 600.
Расстояние от вершины основания до боковой грани
равно 3![]() . Найдите площадь боковой
поверхности пирамиды.
. Найдите площадь боковой
поверхности пирамиды.
Задачи № 4
В правильной четырехугольной пирамиде боковые
грани наклонены к основанию под углом 600, а
расстояние от середины стороны основания до
противоположной боковой грани равно 4![]() . Найдите площадь боковой поверхности.
. Найдите площадь боковой поверхности.
Урок 3.
Индивидуальная контролирующая проверочная работа 4 варианта.
В – 1
- Найдите высоту правильной шестиугольной пирамиды, если сторона ее основания равна а, апофема h
- Сторона основания правильной четырехугольной пирамиды равна а, а высота h. Определить полную поверхность пирамиды.
- Найдите высоту правильной треугольной
пирамиды, у которой боковая поверхность равна
60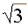 см2, а полная поверхность 108
см2, а полная поверхность 108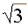 см2.
см2.
В – 2
- Найдите высоту правильной треугольной пирамиды, если сторона ее основания равна а, а апофема h.
- Боковое ребро правильной четырехугольной пирамиды, равное 12 см, образует с плоскостью основания угол в 600. Найдите боковую поверхность пирамиды.
- Найдите высоту правильной треугольной
пирамиды, у которой площадь основания равна
27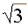 см2, а полная поверхность 72
см2, а полная поверхность 72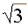 см2.
см2.
В – 3
- Сторона основания правильной четырехугольной
пирамиды равна а. Двугранные углы при
основании равны
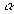 . Определите полную
поверхность.
. Определите полную
поверхность. - Найдите величину двугранного угла при основании правильной четырехугольной пирамиды, если ее боковые ребра наклонены к плоскости основания под углом 300.
- Найдите высоту правильной треугольной
пирамиды, у которой площадь основания равна
27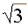 см2, а полная поверхность 72
см2, а полная поверхность 72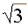 см2.
см2.
В – 4
- Найдите величину двугранного угла при основании правильной четырехугольной пирамиды, если ее боковые ребра наклонены к плоскости основания под углом 600.
- Высота боковой грани правильной четырехугольной пирамиды равна 10 см. Определите полную поверхность пирамиды, если боковая грань наклонна к плоскости основания под углом 600.
- Найдите высоту правильной треугольной
пирамиды, у которой боковая поверхность равна
60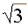 см2, а полная поверхность 108
см2, а полная поверхность 108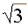 см2.
см2.