Учебная цель: закрепить знания, полученные учащимися на предыдущих уроках
- понятие последовательности;
- нахождение членов последовательности по заданным формулам;
- составление формулы n-го члена;
- решать задачи на нахождение суммы членов.
Воспитательная цель:
- прививать навыки делового общения;
- воспитывать чувство товарищества, взаимовыручки, самостоятельного принятия решения (кроссворд, эстафета, работа в парах, работа по группам);
- воспитывать чувство любви к своей Родине.
Оборудование:
- карточки устного счета; тесты;
- карточки для работ в группах;
- таблица результатов.
Технология: личностно-ориентированный подход.
Ход урока
I. Оргмомент
II. Повторение (решить кросссворд)
По горизонтали
1. Первый из двух стоящих рядом членов последовательности
2. Разность последовательно одинаковых членов
3. Способ задания последовательности
4. Число в арифметической прогрессии
5. Элементы, из которых состоит последовательность
6. Натуральное число, обозначающее место члена в последовательности
По вертикали
1. Функция, заданная на множестве натуральных чисел
7. Вид последовательности
8. Последовательность, содержащая конечное число членов
Дополнительные вопросы к кроссворду:
1. Способы задания последовательности
2. Почему та или иная последовательность называется арифметической прогрессией?
3. Записать на доске формулы, связанные с темой
Работа по карточкам (устно)
1. Найти пятый, десятый член последовательности
2. Найти третий и пятый члены последовательности.
yn = 3 x 2-n
3. Найти номер члена последовательности равного –25.
an = n2 – 10n
4. Перечислить члены последовательности, стоящие между xn-2 и xn+2.
5. Решить первые два теста.
III. Работа по теме “Арифметическая прогрессия”
Решение задания (эстафета)
(класс разбит на 2 варианта, учащиеся по выбору подходят и решают задание).
Данная последовательность является арифметической прогрессией
1, -6…А= -104 /-1,6…А=104/
1. Напишите формулу ее общего члена.
2. Является ли данное число А членом этой прогрессии?
3. Из данной последовательности образовать две новые:
(xn): из членов, стоящих на четных местах
(yn): из членов стоящих на нечетных местах
4. Будет ли (xn) арифметической прогрессией?
5. Будет ли (yn) арифметической прогрессией?
6. Запишите формулу n-го члена для (xn)
7. Запишите формулу n-го члена для (yn)
Решение тестов (3, 4, 5, 6) (см.приложение)
Задачи по выбору:
1. По заданному значению суммы двух членов арифметической прогрессии найти сумму n первых членов арифметической прогрессии.
а) а5 + а9 = 10 n = 13 б) а7 + а15 = 2/3 n = 21 в) а15 + а16 = 4,2 n = 30
2. Найти сумму всех натуральных чисел от 5 до 35 включительно.
3. Найти четвертый член и сумму первых четырех членов арифметической прогрессии в которой а1 = 8 d = 3
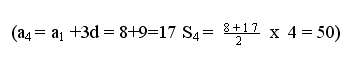
Задача:
Представь, что ты прораб на стройке.
Привезли и выгрузили большое количество труб.
Нужно быстро определить, чтобы закрыть наряд шоферу, сколько привезли труб?
Как ты это сделаешь?
Какое рационализаторское предложение внесешь по транспортировке и выгрузке труб?
(В данном случае нужно выбрать форму контейнера или захвата для выгрузки, чтобы подсчет труб осуществлялся по простым формулам. Один из способов – использовать естественное расположение труб штабелем так, что в каждом верхнем ряду количество оказывается на 1 ед. меньше, чем в предыдущем нижнем, т.е. числа труб в последовательных рядах образуют арифметическую прогрессию, и общее количество подсчитывается по формуле суммы арифметической прогрессии с разностью =1)
Задания на выбор (с выбором правильного ответа)
1. Найти сумму всех нечетных двузначных чисел.
Вопрос: Самое большое озеро Якутии.
Ответ: Неджели – 2700 м.
Моготоево – 2475 м
Большое Токо – 2225 м
2. Найти сумму 25 членов арифметической прогрессии, если а1 = 6 d = 3.
Вопрос: Какой поделочный камень назван в честь притока р. Олекма?
Ответ: Алмаз – 1230; Чароит – 1050; Кварц – 1100.
3. Сколько нужно сложить натуральных чисел, начиная с 25, чтобы их сумма равнялась 196?
Вопрос: Сколько городов в Якутии?
Ответ: количество городов: 10 – 8; 8 – 9; 12 – 7.
(Алдан, Якутск, Нерюнгри, Ленск, Мирный, Олекминск, Среднеколымск, Верхоянск, Вилюйск, Томмот, Покровск, Верхневилюйск).
В арифметической прогрессии (аn) а2 составляет 90% от а1. Сколько % от а1 составляет а4?
Вопрос: Как называется благородный олень Якутии?
Ответ: Лось – 10%; Косуля – 30%; Изюбрь – 70%
Найти S30, an = 2 n + 3
Вопрос: Самый большой хищник Якутии?
Ответ: Лось – 1050; Белый медведь – 1020; Бурый медведь - 1120
Найти сумму первых двадцати членов арифметической прогрессии.
-3; -7;…
Вопрос: Когда Якутия вошла в состав Российского государства?
Ответ: 1632г. - -560; 1917г. - -740; 1922г. - -820
Найти сумму первых пятидесяти членов арифметической прогрессии, если
а1 = 1 а50 = 20
Вопрос: Самый северный остров Якутии?
Ответ: о-ва Де-Лонга – 550; Ляховские о-ва – 525; Медвежьи о-ва – 600
Найти S40, если в арифметической прогрессии а17 + а24 = -5,3
Вопрос: Город, где добывают высококачественный каменный уголь?
Ответ: Якутск - -92; Алдан - -104; Нерюнгри - -106
Тесты (7, 8, 9, 10) (см.приложение).
IV. Итог урока. Рефлексия.
Д\з: составить тесты по теме “Арифметическая прогрессия”.