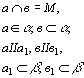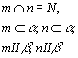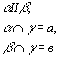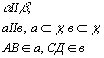Цели урока:
- Ввести понятие параллельных плоскостей.
- Рассмотреть и доказать теоремы, выражающие признак параллельности плоскостей и свойства параллельных плоскостей.
- Проследить применение этих теорем при решении задач.
План урока (записать на доске):
I. Подготовительная устная работа.
II. Изучение нового материала:
1. Взаимное расположение двух плоскостей в пространстве.
2. Определение параллельных плоскостей.
3. Признак параллельности плоскостей.
4. Свойство параллельных плоскостей.
III. Итог урока.
IV. Домашнее задание.
ХОД УРОКА
I. Устная работа
Начать урок хочется с цитаты из философского письма Чаадаева:
“Откуда это чудодейственная мощь анализа в математике? Дело в том, что ум здесь действует в полном подчинении данному правилу”.
Это подчинение правилу мы рассмотрим на следующем задании. Для усвоения нового материала необходимо повторить некоторые вопросы. Для этого надо установить утверждение, которое следует из данных утверждений и обосновать свой ответ:
1) ![]()
2) ![]()
3)![]()
II. Изучение нового материала
1. Как могут располагаться две плоскости в пространстве? Что представляет собой множество точек, принадлежащих обеим плоскостям?
Ответ:
а) совпадать (тогда дело будем иметь с одной
плоскостью, не устраивает);
б) пересекаться, ![]() ;
;
в) не пересекаться (общих точек вообще нет).
2. Определение: Если две плоскости не пересекаются, то они называются параллельными
3. Обозначение: ![]()
4. Приведите примеры параллельных плоскостей из окружающей обстановки
5. Как выяснить параллельны ли какие-либо две плоскости в пространстве?
Ответ:
Можно воспользоваться определением, но это нецелесообразно, т.к. установить пересечение плоскостей не всегда возможно. Поэтому необходимо рассмотреть условие достаточное для того, чтобы утверждать о параллельности плоскостей.
6. Рассмотрим ситуации:
а) если ![]() ?
?
б) если ![]()
![]() ?
?
в) если ![]() ?
?
Почему в а) и б) ответ: "не всегда", а в в)
"да"? (Пересекающиеся прямые определяют
плоскость единственным образом, значит ![]() определены однозначно!)
определены однозначно!)
Ситуация 3 и есть признак параллельности двух плоскостей.
7. Теорема: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
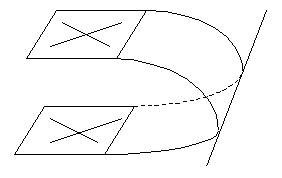 Дано:
Дано:
Доказать: ![]()
Доказательство:
(Обозначения на чертеж наносят учащиеся).
1. Отметим:
. Аналогично:
2. Пусть:.
3. Имеем:Аналогично:
4. Получим: через М проходитпротиворечие с аксиомой планиметрии.
5. Итак:неверно, значит
, ч. и т. д.
8. Решить № 51 (Обозначения на чертеж наносят учащиеся).
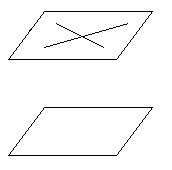 Дано:
Дано:
Доказать: ![]()
Доказательство:
1 способ
1. ![]() Построим
Построим ![]()
2. ![]() ч.
т.д.
ч.
т.д.
2 способ
![]() Ввести
Ввести ![]() через
через ![]() через
через ![]() .
.
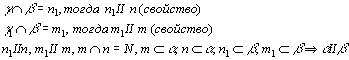
9. Рассмотрим два свойства параллельных плоскостей:
Теорема: Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
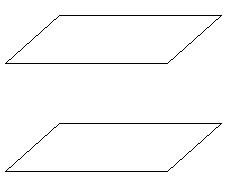 (Достраивают
и наносят обозначение на чертеж сами учащиеся).
(Достраивают
и наносят обозначение на чертеж сами учащиеся).
Дано:
Доказать: ![]()
Доказательство: (разбирают самостоятельно, у доски доказывают на оценку)
1. ![]()
2. ![]() не
параллельна
не
параллельна ![]() тогда
тогда ![]()
3. ![]() (А3)
(А3)
Получили противоречие с условием.
Значит ![]() ч. т.д.
ч. т.д.
Теорема: Отрезки параллельных прямых, заключенных между параллельными плоскостями, равны чертеж используем тот же (свойства 1).
Дано:
Доказать: АВ = СД
Доказательство:
1. ![]()
2. АВСД – параллелограмм, т.к. ![]()
3. из п.2 ![]() АВ = СД ч.т.д.
АВ = СД ч.т.д.
10. Решить № 65 (если успеем) устно, чертеж в учебнике.
III. Итог урока
– Приведите примеры параллельных плоскостей.
– Дайте определение параллельных плоскостей
– По какому признаку устанавливается
параллельность плоскостей,
– Какими свойствами обладают параллельные
плоскости.
IV. Домашнее задание
п. 10–11, стр. 20–22
№ 55, № 58, № 59 – разобраны в учебнике Л.С.Атанасян, выучить формулировки.
№ 49, № 50, № 54(а) – письменно в тетрадях.