Перевод десятичных чисел в двоичную систему счисления

Илифанова Полина Егоровна

Цели:

Образовательные:

познакомить с алгоритмом перевода десятичных чисел в двоичную систему счисления методом деления;
способствовать закреплению данного метода на примерах;

Развивающие:

способствовать развитию логического мышления;
способствовать развитию памяти, внимания;
способствовать развитию грамотной речи;

План проведения урока:

Содержание этапов урока	Виды и формы работы
1. Подготовительный этап.	Приветствие.
2. Актуализация прежних знаний.	Проверка домашнего задания. Устный опрос.
3. Объяснение нового материала.	Беседа с демонстрацией на доске. Конспект.
4. Закрепление изученного материала.	Выполнение заданий по карточкам.
5. Подведение итогов.	Выставление оценок, повторение алгоритмов перевода чисел.
6. Домашнее задание.	п.2.7.2 (учебник для 10-11 классов Н.Д.Угринович), упр. 2.15

Тип урока: изучение нового материала в виде лекции.

Оборудование: карточки с заданиями.

Ход урока

1.Организационный момент.

2.Актуализация опорных знаний.

Двое у доски готовят домашнее задание, параллельно идет устный опрос по вопросам:

1) Проверка домашнего задания:

Упр. 2.13

9₁₀ = 8 + 1 = 2 + 2 = 1001₂

17₁₀ = 16 + 1 = 2 + 2 = 10001₂

243₁₀ = 128 + 64 + 32 + 16 + 2 + 1 = 2 + 2 + 2 + 2 + 2 + 2 = 11110011₂

Устный опрос:

Какие цифры используются в двоичной и десятичной системах счисления?
Какое число является основанием двоичной системы счисления?
Как записывается число 2 в двоичной системе счисления? Почему?
В чем состоит метод разностей?

3. Объяснение нового материала.

На прошлом уроке мы с вами рассмотрели один из способов перевода чисел из десятичной в двоичную систему счисления - метод разностей. Существуют и другие, более эффективные способы. Рассмотрим один из них - метод деления.

Рассмотрим перевод целого десятичного числа в двоичную систему счисления.

Пусть А_ц = а _n-1 х 2 ^n-1 +... + а ₁ х 2 ¹ + а ₀ х 2 ⁰

- поделим А_ц на 2, тогда неполное частное будет а _n-1 х 2 ^n-1 + … +а₁ ,а остаток а₀

- полученное неполное частное опять разделим на 2, остаток от деления будет а₁ и т.д.

- на n-м шаге получим набор остатков а ₀, а ₁, а ₂, ..., а _n-1, которые входят в двоичное представление числа А_ц и совпадают с остатками от последовательного деления данного числа на 2. Но мы получим их в обратном порядке. Нужно только переписать их .

А_ц = а _n-1 а _n-2 ... а ₁ а ₀

Пример 1. Перевести число 11 из десятичной системы счисления в двоичную систему.

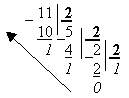Соберем остатки от деления в направлении, указанной стрелкой, начиная с последней единицы и получим число в двоичной системе счисления:

Сравним полученный результат по таблице, которую записали на прошлом уроке.

Пример 2. Если десятичное число достаточно большое, то можно применить следующий вид записи:

соберем остатки от деления в направлении, указанной стрелкой, начиная с последней единицы и получим число в двоичной системе счисления

363₁₀ = 101101011₂

Рассмотрим перевод правильной десятичной дроби в двоичную систему счисления.

Пусть А_ц - правильная десятичная дробь ,тогда его можно записать в виде:

А_др = а _-1 х 2 ^-1 + а _-2 х 2 ^-2 +...

Если А_др умножить на 2 , то в правой части получим а _-1 + а _-2 х 2 ^-1 + а_-3 х 2 ^-2 +...,

где а_-1 - целая часть, она и даст нам старший коэффициент в разложении числа А_др по степеням 2. Оставшуюся дробную часть снова умножим на 2 и получим а _-2 + а_-3 х 2 ^-1 +... , где а_-2 - второй коэффициент после запятой в двоичном представлении числа. Процесс продолжить до тех пор, пока в правой части не получим 0 или не будет достигнута требуемая точность вычислений.

Пример 3.

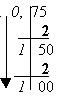
0,75₁₀ = 0,11₂

Проверка:

0,11₂ = 1 х 2 ^-1 + 1 х 2 ^-2 = 0,5 + 0,25 = 0,75₁₀

Пример 4.

Этот процесс может продолжаться бесконечно, его обрывают на том шаге, когда считают, что получена требуемая точность.

А если число смешанное? Тогда нужно отдельно перевести целую часть и отдельно - дробную.

Пример 5. Перевести число 15, 25₁₀

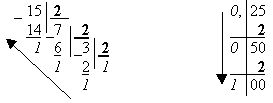
Значит 15,25₁₀ = 1111,01₂

Конспект.

Алгоритм перевода целого десятичного числа в двоичное:

последовательно выполнять деление целого десятичного числа и получаемых целых частных на 2 до тех пор, пока не получится частное, меньшее 2;
записать полученные остатки в обратной последовательности.

Алгоритм перевода правильной десятичной дроби в двоичную:

последовательно выполнять умножение десятичной дроби и получаемых дробных частей произведения на 2 до тех пор, пока не получится нулевая дробная часть или не будет достигнута требуемая точность;
записать полученные целые части произведения в прямой последовательности.

Алгоритм перевода смешанного десятичного числа в двоичное:

перевести целую часть;
перевести дробную часть;
сложить полученные результаты.