Тип урока: Комбинированный урок.
Цели и задачи:
- образовательная – формирование и развитие у учащихся пространственных представлений; выработка навыков решения задач на построение сечений простейших многогранников;
- воспитательная - воспитывать волю и настойчивость для достижения конечных результатов при построении сечений простейших многогранников; воспитывать любовь и интерес к изучению математики.
- развивающая – развитие у учащихся логического мышления, пространственных представлений, развитие навыков самоконтроля.
Оборудование: компьютеры со специально разработанной программой, раздаточный материал в виде готовых чертежей с задачами, тела многогранников, индивидуальные карточки с домашним заданием.
Структура урока:
- Сообщение темы и цели урока (2 мин).
- Инструктирование по выполнению заданий на компьютере (2 мин).
- Актуализация опорных знаний и умений учащихся (4 мин).
- Тестирование с самопроверкой (3 мин).
- Решение задач с объяснением хода решения учителем (15 мин).
- Самостоятельная работа с самопроверкой (10 мин).
- Постановка домашнего задания (2 мин).
- Подведение итогов (2 мин).
Ход урока
1. Сообщение темы и цели урока
После проверки готовности класса к уроку учитель сообщает, что сегодня проводится урок по теме “Построение сечений многогранников”, будут рассмотрены задачи на построение сечений некоторых простейших многогранников плоскостями, проходящими через три точки, принадлежащие ребрам многогранников. Урок будет проходить с использованием компьютерной презентации, выполненной в Power Point.
2. Инструктирование по технике безопасности при работе в компьютерном классе
Учитель. Обращаю ваше внимание на то, что вы приступаете к работе в компьютерном классе, и вам необходимо соблюдать правила поведения и работы за компьютером. Зафиксируйте выдвижные столешницы и следите за правильной посадкой.
3. Актуализация опорных знаний и умений учащихся
Учитель. Для решения многих геометрических задач связанных с многогранниками, полезно уметь строить на рисунке их сечения различными плоскостями, находить точку пересечения данной прямой с данной плоскостью, находить линию пересечения двух данных плоскостей. На предыдущих уроках мы рассматривали сечения многогранников плоскостями, параллельными ребрам и граням многогранников. На этом уроке мы рассмотрим задачи на построение сечений плоскостью, проходящей через три точки, расположенные на ребрах многогранников. Для этого рассмотрим простейшие многогранники. Что это за многогранники? (Демонстрируются модели куба, тетраэдра, правильной четырехугольной пирамиды, прямой треугольной призмы).
Учащиеся должны определить вид многогранника.
Учитель. Давайте посмотрим как они выглядят на экране монитора. От изображения к изображению переходим по нажатию левой клавиши мыши.
На экране одно за другим появляются изображения названных многогранников.
Учитель. Вспомним, что называется сечением многогранника.
Учащийся. Многоугольник, сторонами которого являются отрезки, принадлежащие граням многогранника, с концами на ребрах многогранника, полученный в результате пересечения многогранника произвольной секущей плоскостью.
Учитель. Какие многоугольники могут являться сечениями данных многогранников.
Учащийся. Сечения куба: трех - шести- угольники. Сечения тетраэдра: треугольники, четырехугольники. Сечения четырехугольной пирамиды и треугольной призмы: трех - пяти- угольники.
4. Тестирование с самопроверкой
Учитель. В соответствии с понятием сечения многогранников, знаний аксиом стереометрии и взаимного расположения прямых и плоскостей в пространстве, вам предлагается ответить на вопросы теста. Компьютер оценит вас. Максимальная оценка 3 балла – за 3 правильных ответа. На каждом слайде необходимо нажать кнопку с номером правильного ответа. Вы работаете в паре, поэтому каждый из вас получит одинаковое, указанное компьютером количество баллов. Нажмите указатель перехода на следующий слайд. На выполнение задания отводится 3 минуты.
I. На каком рисунке изображено сечение куба плоскостью ABC?
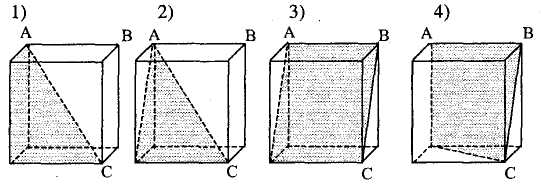
II. На каком рисунке изображено сечение пирамиды плоскостью, проходящей через диагональ основания BD параллельно ребру SA?
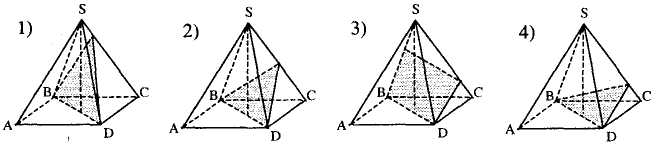
III. На каком рисунке изображено сечение тетраэдра, проходящее через точку М параллельно плоскости ABS?
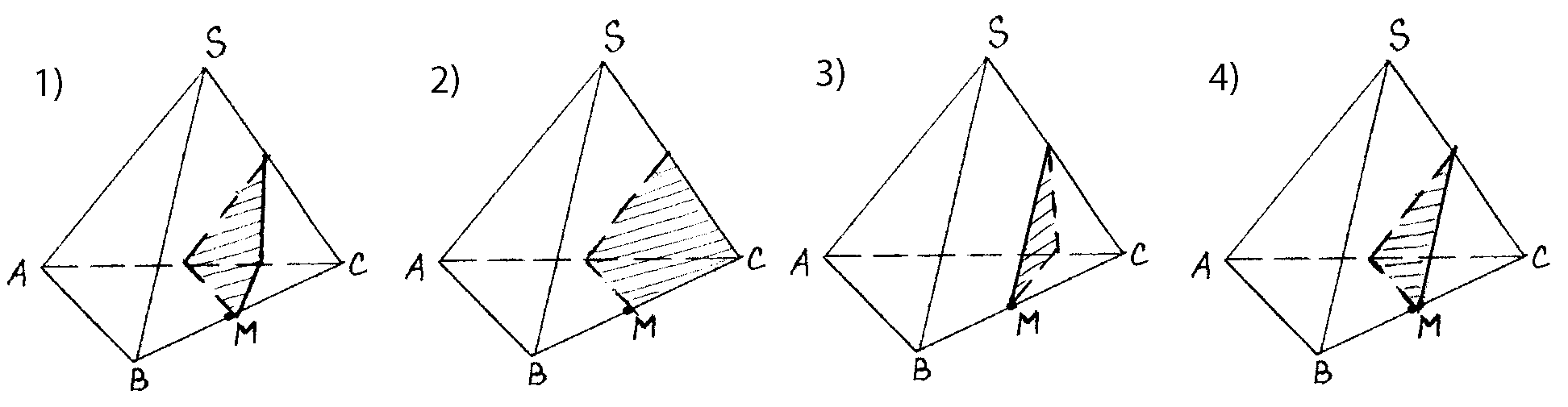
5. Решение задач с объяснением хода решения учителем
Учитель. Перейдем непосредственно к решению задач. Нажмите указатель перехода на следующий слайд.
Задача 1 Данную задачу рассмотрим устно с пошаговым показом построения на экране монитора. Переход осуществляется по клику мыши.
Дан куб ABCDAA1B1C1D1. На его ребре ВВ1 дана точка М. Найти точку пересечения прямой C1M с плоскостью грани куба ABCD.
Рассмотрим изображение куба ABCDAA1B1C1D1 с точкой М на ребре ВВ1 Точки М и С1 принадлежат плоскости ВВ1С1 Что можно сказать о прямой C1M ?
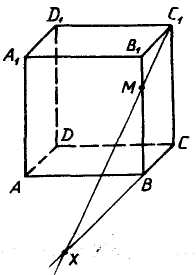
Учащийся. Прямая C1M принадлежит плоскости ВВ1С1
Учитель. Искомая точка X принадлежит прямой C1M, а значит и плоскости ВВ1С1. Каково взаимное расположение плоскостей ВВ1С1 и ABC?
Учащийся. Данные плоскости пересекаются по прямой BC.
Учитель. Значит все общие точки плоскостей ВВ1С1 и ABC принадлежат прямой BC. Искомая точка X должна принадлежать одновременно плоскостям двух граней: ABCD и BB1C1C; из этого следует, что точка X должна лежать на линии их пересечения, т. е. на прямой ВС. Значит, точка X должна лежать одновременно на двух прямых: С1М и ВС и, следовательно, является их точкой пересечения. Построение искомой точки рассмотрим на экране монитора. Последовательность построения вы увидите по нажатию левой клавиши мыши: продолжаем С1М и ВС до пересечения в точке X, которая и есть искомая точка пересечения прямой С1М с плоскостью грани ABCD.
Учитель. Для перехода к следующей задаче воспользуйтесь указателем перехода к следующему слайду. Эту задачу рассмотрим с краткой записью построения.
Задача 2.
а) Построить сечение куба плоскостью,
проходящей через точки А1, М![]() D1C1
и N
D1C1
и N![]() DD1
и б) Найти линию пересечения секущей
плоскости с плоскостью нижнего основания куба.
DD1
и б) Найти линию пересечения секущей
плоскости с плоскостью нижнего основания куба.
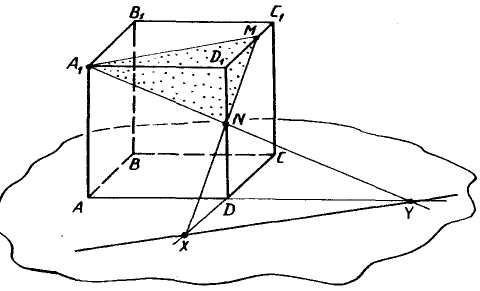
Решение. I. Секущая плоскость имеет с гранью A1B1C1D1
две общие точки А1 и М и,
следовательно, пересекается с нею по прямой,
проходящей через эти точки. Соединяя точки А1
и М отрезком прямой, находим линию
пересечения плоскости будущего сечения и
плоскости верхней грани. Этот факт будем
записывать следующим образом: А1![]() М . Нажимаем
левую клавишу мыши, повторным нажатием будет
построена эта прямая.
М . Нажимаем
левую клавишу мыши, повторным нажатием будет
построена эта прямая.
Аналогично находим линии пересечения секущей плоскости с гранями АА1D1D и DD1С1С. Нажимая клавишу мыши, вы будете видеть краткую запись и ход построения.
Таким образом, A1NМ ? искомое сечение.
Перейдем ко второй части задачи. Найдем линию пересечения секущей плоскости с плоскостью нижнего основания куба.
II. Секущая плоскость с плоскостью основания
куба пересекается по прямой. Чтобы изобразить
эту прямую достаточно найти две точки
принадлежащие данной прямой, т.е. общие точки
секущей плоскости и плоскости грани ABCD.
Опираясь на предыдущую задачу такими точками
будут являться: точка X =![]() . Нажмите клавишу, вы
будете видеть краткую запись и построение. И
точка Y, как вы думаете, ребята, как ее
получить?
. Нажмите клавишу, вы
будете видеть краткую запись и построение. И
точка Y, как вы думаете, ребята, как ее
получить?
Учащийся. Y =![]()
Учитель. Посмотрим на экране ее построение. Нажмите клавишу мыши. Соединяя точки X и Y (Запись X-Y), получим искомую прямую - линию пересечения секущей плоскости с плоскостью нижнего основания куба. Нажмите левую клавишу мыши – краткая запись и построение.
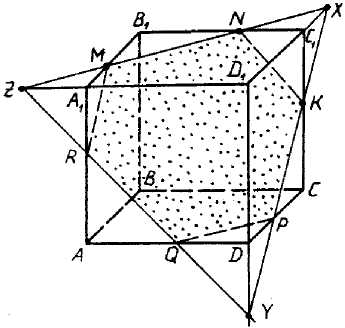
Задача 3 Построить сечение куба
плоскостью, проходящей через точки: ![]()
Так же, нажимая клавишу мыши, вы будете видеть
на экране монитора ход построения и краткую
запись. Опираясь на понятие сечения, нам
достаточно найти в плоскости каждой грани две
точки для построения линии пересечения секущей
плоскости и плоскости каждой грани куба. Точки M
и N принадлежат плоскости А1В1С1
. Соединив их, получим линию пересечения
секущей плоскости и плоскости верхней грани куба
(нажимаем клавишу мыши). Продолжим прямые MN и D1C1
до пересечения. Получим точку Х ,
принадлежащую как плоскости А1В1С1
, так и плоскости DD1C1 (клик
мыши). Точки N и К принадлежат плоскости
ВВ1С1. Соединив их, получим
линию пересечения секущей плоскости и грани ВВ1С1С.
(Клик мыши). Соединяем точки Х и К, и
продолжаем прямую ХК до пересечения с прямой DC.
Получим точку Р и отрезок КР – линию
пересечения секущей плоскости и грани DD1C1C.
(Клик мыши). Продолжая прямые КР и DD1
до пересечения, получим точку Y, принадлежащую
плоскости АА1D1. (Клик мыши). В
плоскости этой грани нам требуется еще одна
точка, которую получаем в результате пересечения
прямых MN и А1D1. Это точка ![]() . (Клик
мыши). Соединяем точки Y и Z, получим
. (Клик
мыши). Соединяем точки Y и Z, получим ![]() и
и ![]() . (Клик
мыши). Соединив Q и Р, R и M, получим
. (Клик
мыши). Соединив Q и Р, R и M, получим ![]() ?
искомое сечение.
?
искомое сечение.
Краткая запись построения:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() ;
;
9) ![]() ;
;
10) ![]() ;
;
11) ![]() ;
;
12) ![]() ;
;
13) ![]() ?
искомое сечение.
?
искомое сечение.
Задача 4. Построить сечение четырехугольной
пирамиды SABCD плоскостью, проходящей через
точки: ![]() .
.
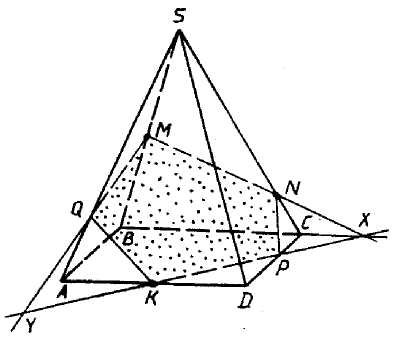
Учитель. Кто желает прокомментировать данную задачу ?
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() ;
;
9) ![]() ;
;
10) ![]() ? искомое сечение.
? искомое сечение.
6. Самостоятельная работа с самопроверкой
Учитель. Предлагаю вам попробовать свои силы в самостоятельном решении подобных задач с записью плана построения. На эту работу отводится 10 минут. По окончании работы вы сверите свое решение с компьютером и сами оцените себя. Каждая задача 1 балл. Полученные баллы вы проставите себе на листы, кроме того впишите результат тестирования. Из этих баллов будет складываться оценка за урок. Во время выполнения вами самостоятельной работы, я выдам вам домашнее задание для закрепления изученного материала.
Учащимся выдаются задания на готовых чертежах по вариантам (Приложение 1). Задачи решаются с записью плана построения. Полученный результат сверяют с решением на компьютере (Приложение 2).
7. Постановка домашнего задания
Во время выполнения самостоятельной работы учитель выдает каждому индивидуальное домашнее задание на карточках:
Задача 1. Построить сечение куба плоскостью,
проходящей через точки ![]() и
и ![]() и найти линию пересечения
секущей плоскости с плоскостью нижнего
основания куба.
и найти линию пересечения
секущей плоскости с плоскостью нижнего
основания куба.
Задача 2. Построить сечение куба плоскостью,
проходящей через точки: ![]() .
.
Задача 3. Построить сечение куба плоскостью,
проходящей через точки ![]() .
.
Задача 4. Построить сечение куба плоскостью,
проходящей через точки: ![]() .
.
3aдача 5. Построить сечение треугольной призмы ![]() плоскостью, проходящей через точки:
плоскостью, проходящей через точки: ![]() .
.
Задача 6. Построить сечение куба плоскостью,
проходящей через точки: ![]() . (Точки М, N и К
лежат на скрещивающихся ребрах.)
. (Точки М, N и К
лежат на скрещивающихся ребрах.)
Задача 7. Построить сечение куба плоскостью,
проходящей через точки: ![]()
Решение домашних задач (Приложение 3).
8. Подведение итогов
Учитель. Сегодня на уроке мы закрепили навыки решения задач на построение сечений простейших многогранников и воспользовались для этого возможностями вычислительной техники. Оценки за урок: объявляются оценки. Всем спасибо.