Исследовательская работа в 10-м классе при изучении темы "Свойства правильного тетраэдра"

Разделы: Математика

План подготовки и проведения занятия:

I. Подготовительный этап:

  1. Повторение известных свойств треугольной пирамиды.
  2. Выдвижение гипотез о возможных, не рассмотренных ранее, особенностях тетраэдра.
  3. Формирование групп для проведения исследований по данным гипотезам.
  4. Распределение заданий для каждой группы (с учётом желания).
  5. Распределение обязанностей по выполнению задания.

II. Основной этап:

  1. Решение гипотезы.
  2. Консультации с учителем.
  3. Оформление работы.

III. Заключительный этап:

  1. Представление и защита гипотезы.

Цели занятия:

  • обобщить и систематизировать знания и умения учащихся; изучить дополнительный теоретический материал по указанной теме; научить применять знания при решении нестандартных задач, видеть в них простые составляющие;
  • формировать навык работы учащихся с дополнительной литературой, совершенствовать умение анализировать, обобщать, находить главное в прочитанном, доказывать новое; развивать коммуникативные навыки учащихся;
  • воспитывать графическую культуру.

Подготовительный этап (1урок):

  1. Сообщение учащегося “Тайны великих пирамид”.
  2. Вступительное слово учителя о разнообразии видов пирамид.
  3. Обсуждение вопросов:
  • По каким признакам можно объединять неправильные треугольные пирамиды
  • Что мы понимаем под ортоцентром треугольника, и что можно называть ортоцентром тетраэдра
  • Существует ли ортоцентр у прямоугольного тетраэдра
  • Какой тетраэдр называют равногранным Какими свойствами он может обладать
  1. В результате рассмотрения разнообразных тетраэдров, обсуждения их свойств уточняются понятия и появляется некоторая структура:

 

 

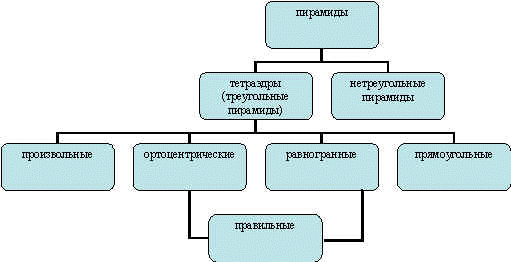
  1. Рассмотрим свойства правильного тетраэдра.(Приложение)

Свойства 1-4 доказываются устно с использованием Слайда1.

 

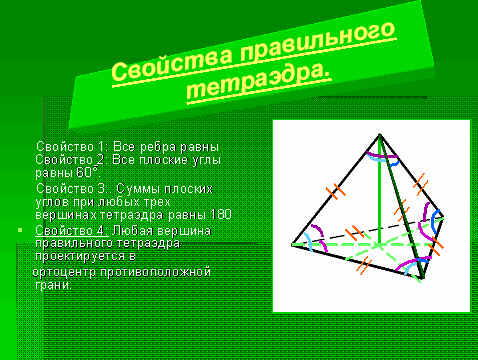
Свойство 1: Все ребра равны.

Свойство 2: Все плоские углы равны 60°.

Свойство 3: Суммы плоских углов при любых трех вершинах тетраэдра равны 180°.

Свойство 4: Если тетраэдр правильный, то любая его вершина проектируется в ортоцентр противоположной грани.

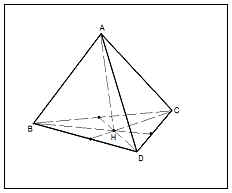
Дано:

ABCD – правильный тетраэдр

AH – высота

Доказать:

H –ортоцентр

 Доказательство:

1) точка H может совпадать с какой-либо из точек A, B, C. Пусть H ?B, H ?C

2) AH + (ABC) => AH + BH, AH + CH, AH + DH,

3) Рассмотрим ABH, BCH, ADH

AD – общая => ABH, BCH, ADH => BH =CH = DH

AB = AC = AD т. H – является ортоцентром ABC

Что и требовалось доказать.

  1. На первом уроке Свойства 5-9 формулируются как гипотезы, которые требуют доказательства.

Каждая группа получает своё домашнее задание:

Доказать одно из свойств.

Подготовить обоснование с презентацией.

II. Основной этап ( в течение недели):

  1. Решение гипотезы.
  2. Консультации с учителем.
  3. Оформление работы.

III. Заключительный этап (1-2 урока):

Представление и защита гипотезы с использование презентаций.

При подготовке материала к заключительному уроку учащиеся приходят к выводу об особенности точки пересечения высот, мы договариваемся называть её “удивительной” точкой.

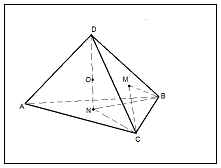
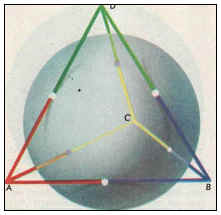
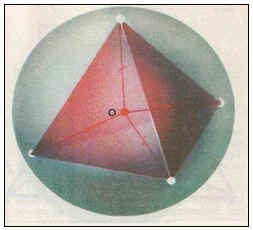
Свойство 5: Центры описанной и вписанной сфер совпадают.

Дано:

DABC –правильный тетраэдр

О1- центр описанной сферы

О - центр вписанной сферы

N – точка касания вписанной сферы с гранью АВС

Доказать: О1 = О

Доказательство:

Пусть OA = OB =OD = OC – радиусы описанной окружности

Опустим ОN + (ABC)

AON = CON – прямоугольные , по катету и гипотенузе => AN = CN

Опустим OM + (BCD)

COM DOM - прямоугольные , по катету и гипотенузе => CM = DM

Из п. 1 CON  COM => ON =OM

ON =OM

ОN + (ABC) => ON,OM – радиусы вписанной окружности.

OM + (BCD)

Теорема доказана. 

Для правильного тетраэдра существует возможность его взаимного расположения со сферой – касание с некоторой сферой всеми своими ребрами. Такую сферу иногда называют “полувписанной”.

Свойство 6: Отрезки, соединяющие середины противоположных ребер и перпендикулярные этим ребрам являются радиусами полувписанной сферы.

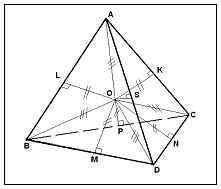
 Дано:

ABCD – правильный тетраэдр;

OLAB, OKAC,

OSAD, ONCD,

OMBD, OPBC,

AL =BL, AK=CK, AS=DS,

BP=CP, BM = DM, CN = DN.

Доказать:

LO = OK = OS = OM = ON =OP

Доказательство.

Тетраэдр ABCD – правильный => AO= BO = CO =DO

Рассмотрим треугольники AOB, AOC, COD, BOD,BOC, AOD.

AO=BO=>?AOB – равнобедренный =>
OL – медиана, высота, биссектриса
AO=CO=>?AOC– равнобедренный =>
ОK– медиана, высота, биссектриса
CO=DO=>?COD– равнобедренный =>
ON– медиана, высота, биссектриса AOB=>                                   AOC= COD=
BO=DO=>?BOD– равнобедренный =>                                     BOD= BOC= AOD
OM– медиана, высота, биссектриса
AO=DO=>?AOD– равнобедренный =>
OS– медиана, высота, биссектриса
BO=CO=>?BOC– равнобедренный =>
OP– медиана, высота, биссектриса
AO=BO=CO=DO
AB=AC=AD=BC=BD=CD

 3) OL, OK, ON, OM, OS, OP - высоты в равных OL,OK,ON,OM,OS, OP радиусы

равнобедренных треугольниках сферы

Следствие:

В правильном тетраэдре можно провести полувписанную сферу.

 Свойство 7: если тетраэдр правильный, то каждые два противоположных ребра тетраэдра взаимно перпендикулярны.

 

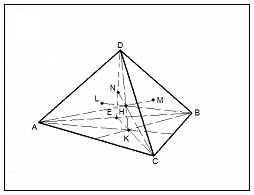
Дано:

DABC – правильный тетраэдр;

H – ортоцентр

Доказать:

AB CD,

AD BC,

AC BD.

 Доказательство:

1) AB CD

DABC – правильный тетраэдр =>?ADB – равносторонний

( ADB) (EDC) = ED

ED – высота ADB => ED +AB,

2) AB + ED ,

ED ( EDC) ,

AB + CE ,=> AB+ (EDC) => AB + CD.

CE (EDC)

Аналогично доказывается перпендикулярность других ребер.

Свойство 8: Шесть плоскостей симметрии пересекаются в одной точке. В точке О пересекаются четыре прямые, проведенные через центры описанных около граней окружностей перпендикулярно к плоскостям граней, и точка О является центром описанной сферы.

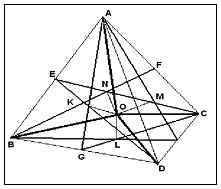
Дано:

ABCD – правильный тетраэдр

Доказать:

О – центр описанной сферы;

6 плоскостей симметрии пересекаются в точке О;

 Доказательство.

1) OL+ (BCD)

CG + BD , т.к. BCD - равносторонний => GO + BD (по теореме о трех GO + BD перпендикулярах)

2) GO + BD

BG = GD, т.к. AG – медиана ABD

?ABD ( ABD)=> ? BOD - равнобедренный => BO=DO

GO (BOD)

( ABD)? (BOD)=BD

KO + ( ABD)

ED + AB , т.к. ABD –равносторонний => OE + AD( по теореме о трёх перпендикулярах)

OE + AB

BE = AE, т.к. DE – медиана ?ABD

ABD (ABD) =>?AOB – равнобедренный =>BO=AO

OE (AOB)

(AOB) (ABD) = AB

ON + (ABC) OF + AC ( по теореме о трёх

BF + AC, т.к. ABC - равносторонний перпендикулярах)

 OF + AC

AF = FC, т.к. BF – медиана ?ABC

ABC (ABC) => AOC - равнобедренный => AO = CO

OF (AOC)

(AOC) ?(ABC) = AC

BO = DO

BO = AO =>AO = BO = CO = DO – радиусы сферы,

AO = CO описанной около тетраэдра ABCD

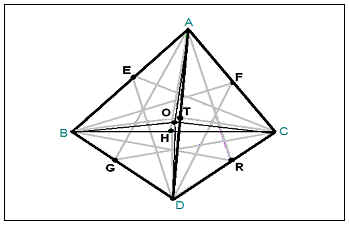
 AO = BO=CO = DO

(ABR)  (ACG) = AO

(BCT)  (ABR) = BO

(ACG)  (BCT) = CO

(ADH)  (CED) = DO

AB + (ABR)(ABR)(BCT)(ACG)(ADH)(CED) (BDF)

BC + (BCT)

AC + (ACG)

AD + (ADH)

CD + (CED)

BD + (BDF)

Следовательно:

Точка О является центром описанной сферы,

6 плоскостей симметрии пересекаются в точке О.

 Свойство 9: Тупой угол между перпендикулярами, проходящими через вершины тетраэдра к ортоцентрам, равен 109°28'

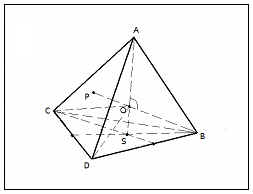
Дано:

ABCD – правильный тетраэдр;

O – центр описанной сферы;

Доказать:

AOB = 109°28'

 Доказательство:

1)AS – высота

ASB = 90o OSB прямоугольный

2)(по свойству правильного тетраэдра)

3)AO=BO – радиусы описанной сферы

4) 70°32'

5)

6) AO=BO=CO=DO =>?AOD=?AOC=?AOD=?COD=?BOD=?BOC

(по свойству правильного тетраэдра)

=>AOD=AOC=AOD=COD=BOD=BOC=109°28'

Это и требовалось доказать.

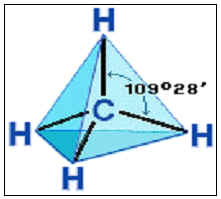
 Интересен тот факт, что именно такой угол имеют некоторые органические вещества: силикаты и углеводороды.

В результате работы над свойствами правильного тетраэдра учащимся пришла мысль назвать работу “Удивительная точка в тетраэдре”. Были предложения рассмотреть свойства прямоугольного и равногранного тетраэдров. Таким образом, работа вышла за рамки урока.

Выводы:

“Удивительная” точка в правильном тетраэдре имеет следующие особенности:

  • является точкой пересечения трех осей симметрии
  •  является точкой пересечения шести плоскостей симметрии
  •  является точкой пересечения высот правильного тетраэдра
  •  является центром вписанной сферы
  •  является центром полувписанной сферы
  •  является центром описанной сферы
  •  является центром тяжести тетраэдра
  • является вершиной четырех равных правильных треугольных пирамид с основаниями – гранями тетраэдра.

 Заключение.

( Учитель и учащиеся подводят итоги занятия. С кратким сообщением о тетраэдрах, как структурной единице химических элементов, выступает один из учащихся.)

Изучены свойства правильного тетраэдра и его “удивительная” точка.

Выяснено, что форму только такого тетраэдра, имеющего все выше перечисленные свойства, а также “идеальную” точку, могут иметь молекулы силикатов и углеводородов. Или же молекулы могут состоять из нескольких правильных тетраэдров. В настоящее время тетраэдр известен не только как представитель древних цивилизации, математики, но и как основа строения веществ.

Силикаты – солеобразные вещества, содержащие соединения кремния с кислородом. Их название происходит от латинского слова “силекс” – “кремень”. Основу молекул силикатов составляет атомные радикалы , имеющие форму тетраэдров.

Силикаты – это и песок, и глина, и кирпич, и стекло, и цемент, и эмаль, и тальк, и асбест, и изумруд, и топаз.

Силикаты слагают более 75 % земной коры (а вместе с кварцем около 87%) и более 95% изверженных горных пород.

Важной особенностью силикатов является способность к взаимному сочетанию (полимеризации) двух или нескольких кремнекислородных тетраэдров через общий атом кислорода.

Такую же форму молекул имеют предельные углеводороды, но состоят они, в отличии от силикатов, из углерода и водорода. Общая формула молекул

К углеводородам можно отнести природный газ.

Предстоит рассмотреть свойства прямоугольного и равногранного тетраэдров.

Литература.

  • Потапов В.М., Татаринчик С.Н. “Органическая химия”, Москва 1976г.
  • Бабарин В.П. “Тайны великих пирамид”, Санкт-Петербург, 2000г.
  • Шарыгин И. Ф. “Задачи по геометрии”, Москва, 1984г.
  • Большой энциклопедический словарь.
  • “Школьный справочник”, Москва, 2001г.