Предметные цели:
создать методическими средствами психолого-педагогические условия для усвоения понятий:
- БУГП
- СУММА БУГП
и применения их при решении ключевых задач:
- Алгоритм распознавания БУГП
- Вычисление суммы БУГП.
Цели личностного развития:
установление содержательных связей БУГП с элементами субъектного опыта учащихся в изучении математики по линиям тождественных преобразований, уравнений и действительных чисел.
Ход занятия (занятие состоит из 2-х уроков)
Урок 1.
1 этап: Диагностика усвоения материала по теме: “Действия с иррациональными числами”.
Самостоятельная работа, которая выполняется индивидуально каждым учащимся. Оперативная обратная связь осуществляется с помощью разбора решений примеров непосредственно по окончании самостоятельной работы.
Содержание самостоятельной работы:
![]()
![]()
![]()
![]()
![]()
(Задания приведены с ответами).
По окончании работы проводится анализ результатов работы и оперативный разбор ошибок.
2 этап. Актуализация знаний, необходимых для изучения нового материала.
Работа осуществляется в форме фронтальной беседы с элементами организации поисковой деятельности. Полученные результаты фиксируются в тетрадях.
Содержание фронтальной работы:
1. Повторение:
а) определения понятия геометрической прогрессии (ГП);
б) формулы n-ого члена ГП;
в) формулы суммы n первых членов ГП.
2. Получение нового результата:
Рассмотрим формулу суммы n первых членов ГП:
![]() .
.
При ![]() эту формулу можно переписать в виде:
эту формулу можно переписать в виде: ![]() или
или ![]() , из
чего следует формула
, из
чего следует формула
Положим в этом равенстве ![]() , тогда получим
, тогда получим
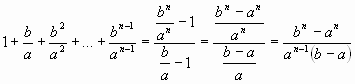 ,
домножим обе части равенства на
,
домножим обе части равенства на ![]() ,
получим
,
получим
![]() , а
отсюда вытекает полезное тождество:
, а
отсюда вытекает полезное тождество:
(Доказательство приведенных формул см. Виленкин Н.Я. и др. “Алгебра и математический анализ. 10 класс”, М., “Просвещение”, 1992г., стр.45).
В результате обсуждения, в процессе которого осуществляется конкретизация вновь полученного обобщенного знания, учащиеся приходят к выводу, что ранее изученные формулы разности квадратов и суммы и разности кубов представляют собой частные случаи выведенных формул:
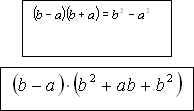
Таким образом, удаётся установить содержательную связь БУГП с линией тождественных преобразований.
3 этап. Создание мотивации для формирования понятий БУГП и суммы БГУП.
Особенный интерес представляет обсуждение наглядной демонстрации существования суммы бесконечного числа слагаемых. Работа осуществляется фронтально, используются элементы исследовательской деятельности.
Содержание этапа:
1. В процессе введения определения БУГП рассматриваются особенности ГП с ¦q¦ < 1. Затем формулируется определение БУГП и решаются ключевые задачи распознавания БУГП:
а) в условии задана ГП; выяснить, является ли она БУГП;
б) в условии задана последовательность; выяснить, является ли она БГУП.
Вторая задача соответствует более высокому уровню сложности: сначала требуется выяснить, выяснить, является ли последовательность ГП;
затем - является ли она БУГП?
1) ![]() ;
;
2) ![]() .
.
Эти задачи могут быть рассмотрены как а) и как б). В процессе закрепления используются упражнения:
15 (3)
Доказать, что ГП является бесконечно убывающей:![]() :-27, -9,
-3,…
:-27, -9,
-3,…
16(3)
Выяснить, является ли ГП бесконечно убывающей: ![]()
(см.Алимов и др.)
Для введения понятия суммы БУГП целесообразно продолжить обсуждение задачи 2) и представить сумму слагаемых с помощью графической интерпретации:
Вывод формулы суммы БУГП проводится в соответствии с материалом учебника Ш.А.Алимов и др. “Алгебра и начала анализа.10-11”, М., “Просвещение”, 2003г., стр.11-14.
Обсуждение полученного результата создает условия для психологического принятия наличия конечной суммы бесконечного числа слагаемых.
Подводятся промежуточные итоги, на доску выносятся основные результаты.
Урок 2 (продолжение).
4 этап. Формирование алгоритма вычисления суммы БУГП.
Работа организована индивидуально у доски и в тетрадях с дифференцированной степенью самостоятельности. Критерием достижения положительного результата этапа является знание всеми учащимися алгоритма нахождения суммы БУГП. Коррекция осуществляется с помощью взаимопроверки. Используются упражнения
18(1,2) Найти сумму БУГП:
1. ![]() Ответ:
Ответ:![]()
2. ![]() ,
Ответ:
,
Ответ: ![]()
а также упражнения из дидактических материалов по алгебре и началам анализа Б.Г.Зива и В.А. Гольдича, с/р №2, упражнения 1 из вариантов 1 и 2.
Найти сумму БУГП:
1. ![]() Ответ: 40,5
Ответ: 40,5
2. ![]() Ответ: 32.
Ответ: 32.
Желающим, справившимся с общим заданием раньше других, предлагается обратная задача:
Известна сумма БУГП и второй член прогрессии. Нужно найти первый член прогрессии и знаменатель:
дано: ![]() =-0,5; S=1,6;
=-0,5; S=1,6;
найти q и ![]() .
.
За самостоятельное решение этой задачи выставляется отдельная оценка.
5 этап. Первичное обобщение и включение нового знания в систему субъектного опыта учащихся.
Установление содержательных взаимосвязей БУГП с линиями уравнений и действительных чисел.
Фронтально решается задача распознавания БГУП. С помощью этой задачи, с одной стороны, осуществляется диагностика достижения положительного результата предыдущих этапов урока, с другой стороны, полученные результаты позволяют осуществить содержательные взаимосвязи по выше указанным линиям.
Из предложенных последовательностей выбрать БУГП:
1) ![]() =3;
q=2.
=3;
q=2.
2) ![]() =-4;
q=
=-4;
q=![]() .
.
3) 4;2;1; и т.д.;
4)![]() =1; q=x; x>2;
=1; q=x; x>2;
5)![]() =
=![]() ; q=
; q=![]() .
.
6) ![]() =
=![]() ; q=
; q=![]() .
.
7) ![]() =
=![]() ; q=
; q=![]()
8) ![]() =1; q=x; ¦x¦<1.
=1; q=x; ¦x¦<1.
Таковыми являются 2); 3); 5); 6); 7) и 8).
Сначала найдём сумму БУГП из задания 8). Для этого запишем сумму членов прогрессии и воспользуемся формулой суммы БУГП. Получим:
1+![]() +
+![]() + …+
+ …+![]() + …=
+ …= ![]() .
.
Установление содержательных взаимосвязей БУГП с линией уравнений
Сравните полученный результат с уравнением и воспользуйтесь при его решении полученным результатом:
Уравнение 1) ![]() ; ¦x¦<1.
; ¦x¦<1.
Заметим, что если к обеим частям равенства прибавить 1, то можно воспользоваться полученным выше результатом:
![]()
![]() .
.
Итак, мы получили дробное рациональное уравнение, алгоритм решения которого известен школьникам.
Уравнение 2) 2![]() + 1 +
+ 1 +![]() -
- ![]() +
+ ![]() -
- ![]() + …=
+ …= ![]()
¦x¦<1.
Решение уравнения 1) проводится учеником на доске, уравнение 2 предлагается для самостоятельной работы дома.
Делается весьма неожиданный вывод о том, что сумма БГУП даёт возможность решения некоторых уравнений, имеющих бесконечное число членов.
Таким образом, удаётся установить содержательную связь БУГП с линией уравнений.
Установление содержательных взаимосвязей БУГП с линией действительных чисел.
К доске приглашаются 3 ученика для решения задач 1-3.
1)![]() =
=![]() ; q=
; q=![]() .
.
Сначала находим сумму БУГП по формуле
S=![]() =
=![]() .
.
Затем попытаемся осмыслить, что представляет собой сумма членов этой прогрессии, если её члены записать в виде десятичных дробей:
0,3+0,03+0,003+….=0,3333…=0,(3).
Таким образом, видим, что с помощью формулы суммы БУГП можно осуществлять переход от записи действительного числа в виде бесконечной периодической дроби к записи в виде обыкновенной дроби.
2) ![]() =
=![]() ; q=
; q=![]() .
.
Эта задача носит дублирующий характер и используется для создания условий лучшего осмысления сформулированного вывода.
3) ![]() =
=![]() ; q=
; q=![]()
Решение этой задачи помогает понять, сколько десятичных знаков содержит период дроби, какие особенности решения возникают в связи с этим.
Решение этих задач даёт возможность установления содержательной связи БУГП с линией действительного числа.
После решения этих задач подводятся итоги урока, предлагается домашнее задание:№20,21(2,4), 22(2), 23(2) из учебника Алимова.
Этап 6. Диагностика достижения положительного результата урока.
Предлагается срезовая работа, которая позволяет оценить достижение всеми учащимися уровня образовательного стандарта.
Вариант 1.№№ 13(1); 15(1); 18(1); 19(1); 20(1).
Вариант 2.№№ 13(2); 15(2); 18(2); 19(2); 20(2).
Решение проводится учащимися в тетрадях, проверяются только специальные бланки (Приложение 1), в которые вписываются ответы. Данная форма позволяет осуществить оперативную обратную связь и, в случае необходимости, провести коррекцию.
Подводятся окончательные итоги урока, сообщаются и комментируются оценки, полученные школьниками.
Приложение 1.
| Класс | Фамилия, имя. | Оценка: | ||||
| № задания | 1 | 2 | 3 | 4 | 5 | |
| Ответ | ||||||