У попа была собака, он ее любил.
Она съела кусок мяса, он ее убил.
Камнем придавил, и на камне написал:
“У попа была собака...””
Детская считалка
Понятие рекурсии. Виды рекурсии.
Рекурсией называется ситуации, когда процедура или функция обращается к себе самой прямо или косвенно. Соответственно говорят о прямой ли косвенной рекурсии. При прямой рекурсии процедура содержит вызов себя в собственном теле, например:
ЭТО процедура 1
….
ЕСЛИ … ТО процедура 1
….
КОНЕЦ
Косвенная рекурсия образуется цепочкой процедур, и эта цепочка замыкает себя в рекурсивное кольцо, например:
ЭТО процедура_1
….
… процедура_2
….
КОНЕЦ
ЭТО процедура_2
….
… процедура_3
….
КОНЕЦ
ЭТО процедура_3
….
… процедура_1
КОНЕЦ
В данном примере “процедура_1” является рекурсивной, так как вызывает сама себя. Правда этот вызов не прямой, а косвенный, через обращение к процедурам “процедура_2” и “процедура_3”. Понятно, что каждая из процедур рекурсивной цепочки является рекурсивной.
Прямая рекурсия всегда предпочтительней косвенной не в смысле эффективности выполнения, а в смысле наглядности записи (читателю программы проследить косвенную рекурсию сложнее).
Вообще, рекурсивным называется любой объект, который частично определяется через себя.
В рекурсивном определении должно присутствовать ограничение, граничное условие, при выходе на которое дальнейшая инициация рекурсивных обращений прекращается.
Приведем примеры рекурсивных определений.
Пример 1. Классический пример, без которого не обходятся ни в одном рассказе о рекурсии, - определение факториала. С одной стороны, факториал определяется так:
n! = 1*2*3*…*n.
С другой стороны, факториал можно определить следующим образом:
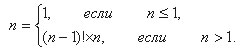
Граничным условием в данном примере является n < 1.
Пример 2. Определим функцию K(n), которая возвращает количество цифр в заданном натуральном числе n.
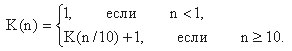
Обращение к рекурсивной подпрограмме (процедуры или функции) ничем не отличается от вызова любой другой подпрограммы. При этом при каждом новом рекурсивном обращении в памяти создается новая копия подпрограммы со всеми локальными переменными. Такие копии будут порождаться до выхода на граничное условие. Очевидно, в случае отсутствия граничного условия, неограниченный рост числа таких копий приведет к аварийному завершению программы за счет переполнения стека (стек - область памяти, в которой хранится состояние вызывающей подпрограммы).
Порождение все новых копий рекурсивной подпрограммы до выхода на граничное условие называется рекурсивным спуском. Максимальное количество копий рекурсивной подпрограммы, которое одновременно может находиться в памяти компьютера, называется глубиной рекурсии. Завершение работы рекурсивных подпрограмм, вплоть до самой первой, инициировавшей рекурсивные вызовы, называется рекурсивным подъемом.
Реализуем приведенные выше рекурсивные определения в виде функций и процедур на языке Pascal.
Пример 1.
Пример программы с функцией
uses crt;
var f: longint: n: integer;
function factorial(n: integer):longint;
begin
if (n=0) or (n=1)
then factorial:=1
else factorial:= factorial(n-1)*n;
end;
begin
clrscr;
write(‘n=’); readln(n);
f:=factorial(n);
writeln (n,’! = ‘, f);
readln;
end.
Пример программы с процедурой
uses crt;
var f: longint: n: integer;
procedure factorial(n: integer; var f: longint);
begin
if (n=0) or (n=1)
then f:=1
else factorial (n-1, f);
f:=f*n;
end;
begin
clrscr;
write(‘n=’); readln(n);
factorial (n, f);
writeln (n,’! = ‘, f);
readln;
end.
Пример 2.
Функция
function K(n: longint):byte;
begin
if n<10
then K:=1
else K:=K(n div 10) +1;
end;
Процедура
procedure K(n: longint; var s: byte);
begin
if n<10 then s:=1
else K( n div 10, s);
s:=s+1;
end;
В приведенных выше примерах программ действия выполняются на рекурсивном подъеме (прямая рекурсия).
А теперь рассмотрим рекурсивные графические алгоритмы, проведем анализ их сложности и эффективности.
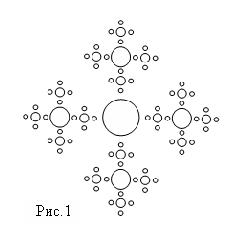
Пример 3. Напишите программу построения изображения, представленного на рис.1.
Самостоятельная работа №1.
Задание 1. По аналогии прим. 2 определите функцию S(n), вычисляющую сумму цифр заданного натурального числа.
Задание 2. Реализуйте в виде процедуры и функции рекурсивное определение примера задания №1.
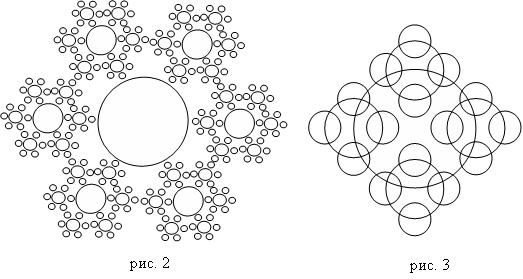
Задание 3. Напишите программу построения изображения, представленного на рис. 2 и 3.
Фрактальные кривые.
Понятие фрактала. Многие объекты окружающего мира обладают свойством “самоподобия”. Так, строение Вселенной от метагалактики до атома описывается сходными моделями типа “ядро – спутники”; строение гористой поверхности или изрезанность морского берега выглядят примерно одинаково и с космической высоты, и с высоты птичьего полета, и с уровня человеческого роста. Все отличие лишь в разрешающей способности восприятия изображения. Вообразим съемку береговой линии кинокамерой с трансфокатором, имеющим регулируемое, но конечное угловое разрешение. При “наезде” камеры на объект взору открываются неразличимые ранее фрагменты, сходные по структуре с фрагментами предыдущего уровня. Такой процесс укрупнения масштаба изображения принципиально отличается от увеличения фотографии по е негативу или от растяжения выделенного фрагмента растровой картинки, при которых увеличивается зернистость без появления новых более мелких фрагментов.
Математическое описание бесконечно дробимых объектов уравнениями линий или поверхностей чрезвычайно громоздко из-за необъятного количества мельчайших объектов. Для преодоления этой трудности математиком Исследовательского центра корпорации IBM Бенуа Мандельбротом в 1975 году был введен термин “фрактал” (от латинского fractus – раздробленный, разбитый, состоящий из фрагментов), а в 1982 году опубликована основополагающая книга “Фрактальная геометрия природы”, где описаны фрактальные множества, их свойства, методы получения и изображения.
В машинной графике фракталы применяются при генерации искусственных облаков, гор, поверхности моря. Образы фракталов похожи на природные объекты — деревья, растения, узоры, звездные скопления т.п. Фракталы позволяют создавать с помощью нескольких коэффициентов линий и поверхности очень сложной формы.
Ниже рассмотрим некоторые из этих фрактальных множеств.
Итак, займемся построением геометрических узоров. Программы, описываемые здесь, основаны на идеях “черепашьей графики”. “Черепаха” - это вектор с началом в текущем указателе, показывающий направление очередного перемещения из текущей точки и оставляющий при перемещении позади себя след. Что можно делать с “черепахой”? Ее можно поворачивать на заданный угол и перемещать на заданное расстояние.
Пример 4. Начнем с рекурсивной программы рисования кривой Коха.
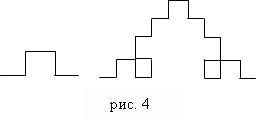
Процесс формирования кривой Коха состоит в следующем – отрезок разбивается на три равные части, и на средней части отрезка строится, например, квадрат (см. рис. 4) или равносторонний треугольник. Для простоты рассмотрим кривую Коха с квадратом. На рис. 4 изображены кривые Коха первого и второго порядка. Для рисования кривой Коха используются только повороты на +90° и -90° и смещения вдоль прямолинейных отрезков. Алгоритм рисования кривой Коха можно записать следующим образом:
- нарисовать прямолинейный отрезок заданной длины;
- повернуть на +90°;
- нарисовать прямолинейный отрезок заданной длины;
- повернуть на -90°;
- нарисовать прямолинейный отрезок заданной длины;
- повернуть на -90°;
- нарисовать прямолинейный отрезок заданной длины.
Затем эта последовательность вновь применяется к каждому прямолинейному участку построенной ломаной линии. Интересной особенностью фрактальных объектов является повторение особенностей их структуры при переходе к любому масштабу.
Программу, реализующую кривую Коха см. в файле Primer_4. pas.
Прямолинейные отрезки, начинающиеся из текущей точки и оканчивающиеся в точке с заданными координатами, в программе рисуются процедурой Linerel модуля Graf. Процедура draw (x,y: integer; dlina:word) является рекурсивной, она строит кривую Коха. Параметрами этой процедуры являются x и y (эти два числа задают единичный вектор в направлении очередного смещения) и величина смещения dlina.
Пример 5. “Множество Кантора”. На первый взгляд, кажется, что “множество Кантора” (см. рис. 5) состоит из большого квадрата и квадратов, нарисованных с помощью множества операторов Line.
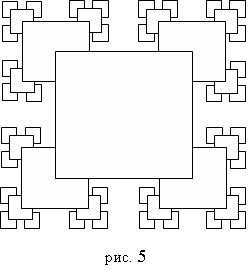
Но при детальном рассмотрении можно заметить, что данный рисунок образован квадратами. Каждый следующий квадрат в четыре раза меньше предыдущего. Центр каждого следующего квадрата расположен в вершине предыдущего квадрата и т.д. Так как рисунок состоит из однотипных элементов, и есть явная зависимость, как размеров, так и положения, следовательно, при создании данного рисунка можно использовать в программе рекурсию.
Алгоритм рисования “множества Кантора”:
- построить большой квадрат, внутреннюю часть которого закрасим каким-либо цветом;
- на его вершинах, как на центрах рисуются квадраты, в четыре раза меньшие первоначального;
- это повторяется для каждого оставшегося квадрата (n), причем бoльшие квадраты перекрывают меньшие.
Программу, реализующую множество Кантора см. в файле primer_5. pas.
Этот пример можно было бы решить и без использования рекурсии, но тогда пришлось бы просчитывать координаты каждого прямоугольника, что заняло бы много времени. Ещё сложнее было бы добиться пропорций рисунка, его равномерного распределения относительно краёв экрана. Да и сама программа заняла бы не одну страницу.
Данная программа даёт возможность изменения количества уровней n (глубину рекурсии), а так же размеры квадратов.
Пример 6. Самым знаменитым примером площадного геометрического фрактала является треугольник Серпинского (см. рис.6), строящийся путем разбиения треугольника, необязательно равностороннего – средними линиями на четыре подобных треугольника, исключением центрального и рекурсивного разбиения угловых треугольников до получения площадных элементов желаемого разрешения.
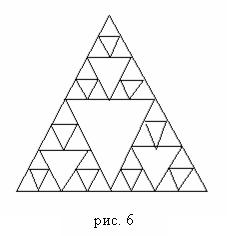
Алгоритм построения треугольника Серпинского довольно прост:
- строится большой внешний треугольник (А);
- строится треугольник, получающийся при соединении середин сторон большого треугольника (Б);
- строятся треугольники, получающиеся аналогично элементу Б, но в качестве большого треугольника берутся треугольники, образованные элементами А и Б.
Изображение состоит из однотипных элементов, связанных между собой зависимостью каждого следующего элемента от координат предыдущего
На рис. 6 представлено изображение, состоящее из трех уровней, а данная программа позволяет рисовать изображение в зависимости от введённого пользователем n уровней.
Программу, реализующая треугольник Серпинского см. в файле primer_6.pas. Преимущество использования рекурсии очевидно - без рекурсии построение такого рисунка состоящего более чем из шести уровней весьма проблематично, а рекурсия позволяет увеличивать количество уровней, не ограничиваясь минимальными размерами самого нижнего уровня. Например, с помощью этой программы можно увеличить количество уровней до пятнадцати при этом будет ощутима только некоторая задержка при выводе изображения на экран, а вот без рекурсии такой рисунок построить будет практически невозможно, так как изображение будет состоять более чем из тридцати одной тысячи треугольников.
Самостоятельная работа №2.
Спирали – это геометрические фигуры, у которых каждая последующая сторона немного больше предыдущей. Спираль является ярким примером графической рекурсии.
Задание 4. а) Разработайте программу построения изображения “Спираль”, представленного на рис. 7.
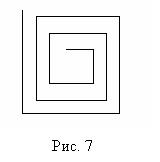
Примечание.
В изображении можно заметить ряд закономерностей:
- построение начинается из “середины” рисунка;
- каждый следующий отрезок увеличивается на определённую величину;
- все отрезки либо вертикальные, либо горизонтальные;
- при рисовании происходит последовательное построение сходных элементов с изменяющимися параметрами следовательно, данный рисунок можно построить с использованием рекурсии, вместо отрезков в программе строятся векторы.
б*) разработайте программу, в которой, кроме стороны, задан еще и угол витков спирали, при увеличении угла можно получить довольно интересные изображения (см. файл Приложение_1.doc).
Решение олимпиадных задач
А сейчас попытаемся применить свои теоретические знания и небольшой, но надеюсь, полезный опыт по созданию рекурсивных программ, на практике. Вам предлагается принять участие в разборе олимпиадных задач, одним из вариантов решения которых является использование рекурсивного алгоритма.
При изучении этого материала можно пойти двумя путями: 1) внимательно изучить предложенный ниже материал, а затем, посмотрев программы для демонстрации, выполнить задания самостоятельной работы №3; 2) попытаться самим придумать и реализовать в Паскале алгоритмы предложенных заданий.
Пример 7. “Снежинка”. Разработайте программу, которая обеспечивает рисование снежинки (рис. 8), количество звеньев и ветвей, коэффициент уменьшения каждого звена ветви задаются пользователем.
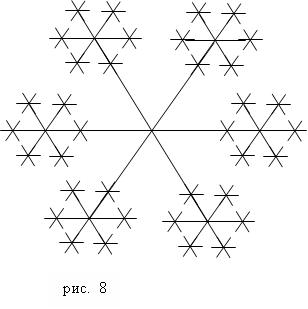
На рисунке изображена снежинка, состоящая из 3 звеньев и 6 ветвей.
Алгоритм работы над задачей:
- Определим, какие данные нужны для рисования снежинки и введем обозначения: n – количество звеньев снежинки, p – количество ветвей снежинки, l – длину (в точках) ветви внутреннего звена, t - коэффициент уменьшения каждого звена.
- Центр снежинки расположим в центре экрана монитора (320, 240).
- Начинаем рисовать из центра снежинки: рисуем первый (длины l) отрезок, далее, если это не последнее звено, то рисуем отрезок длины l*t следующего звена, и так до тех пор, пока не нарисуем отрезок последнего звена (l*tn-1).
- На последнем звене дорисовываем самую маленькую снежинку.
- Возвращаемся на предпоследний отрезок и дорисовываем самое маленькое звено со снежинкой.
- И так продолжаем до тех пор, пока не нарисуем всю снежинку. Эта логика рисования легко реализуется с помощь рекурсии.
Программу, реализующую “Снежинку” см. в файле primer_7.pas. В данной программе предложено два уровня работы: Demo – выводит на экран монитора снежинку с уже заданными параметрами; во втором варианте необходимо сначала ввести параметры (при работе с данной программой обратите внимание на ограничения, накладываемые на ввод данных).
Пример 8 “Ветка”. Разработайте программу построения изображения (см. рис. 9). Длина первоначального звена, коэффициент уменьшения следующих звеньев задаются пользователем.
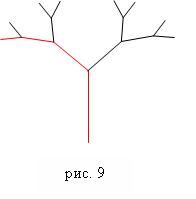
Алгоритм работы над задачей:
- Введем обозначения: n – количество звеньев ветки, длина первоначального (вертикального) отрезка ветки (в точках) - dl, коэффициент уменьшения каждого звена - t .
- Начинаем рисовать с первоначального (вертикального) отрезка, далее, если это не последнее звено, просчитывается длина следующего отрезка и строится этот отрезок; так продолжается до тех пор, пока не прорисуются все n звеньев (см. рис. 10 – красная часть рисунка).
- Далее аналогично рисованию снежинки – прорисовывается левая часть ветви, а затем правая.
Программу, реализующую “Ветку” см. в файле primer_8.pas.
При работе с данной программой обратите внимание на ограничения, накладываемые на ввод данных: n - количество звеньев (>1); dl - длина первоначального отрезка в точках, брать 10 точек …(начните со 100); 0<m<1.
Самостоятельная работа №3
Задание 5. Разработайте программы построения изображений, представленных на рис. 10 и 11 с использованием рекурсии и без нее. Укажите достоинства и недостатки каждой из программ.
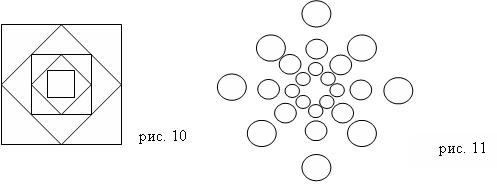
Важно:
1) При выполнении программ на своем компьютере обратите внимание на строку программы, где происходит инициализация графики. Возможно, папка BGI у Вас находится в другом месте.
2) Некоторые “правила предосторожности” при работе с рекурсивными функциями и процедурами:
- Рекомендуется компилировать программу с директивой {$S+}. Эта директива включает проверку переполнения стека. Если в процессе выполнения программы происходит переполнение стека, вызов процедуры или функции, откомпилированной с опцией {$S+}, приводит к завершению работы программы, а на дисплей выдается сообщение об ошибке.
- Полезно также использовать директиву {$R+}, включающую проверку диапазона переменных.
- В начале каждой процедуры (функции), вызываемой рекурсивно, можно поместить строку if keypressed then halt. В этом случае при зависании программы вместо перезагрузки будет достаточно нажать любую клавишу.
Глубина рекурсии (количество рекурсивных вызовов) должна быть конечной, то есть последовательность рекурсивных обращений к функции должна обязательно выходить на определенное значение. Позаботиться об этом должен программист, выбирающий или разрабатывающий рекурсивный алгоритм.
Итоги:
Некоторые программисты считают, что рекурсия – это сердце и душа языка Паскаль. И, думается, не зря. Рекурсивные программы более компактны, и они зачастую становятся более легкими для понимания и написания. В данной теме была сделана попытка выяснить характерные особенности построения рекурсивных графических алгоритмов, оценить их достоинства и недостатки, а также реализовать их на Паскале.