Цели урока:
- ознакомление учащихся с новым видом последовательности – бесконечно убывающей геометрической прогрессией;
- формулирование начального представления о пределе числовой последовательности;
- знакомство с ещё одним способом обращения бесконечных периодических дробей в обыкновенные с помощью формулы суммы бесконечно убывающей геометрической прогрессии.
Ход урока
1. Проверка домашнего задания.
1) Проверка основных формул, связанных с арифметической и геометрической прогрессиями. Два ученика готовят записи формул у доски.
2) Остальные учащиеся выполняют математический диктант по теме «Формулы суммы».
Задания:
№1. Найдите сумму первых пяти членов арифметической прогрессии, если её первый член равен 6 (1-й вариант), -20 (2-й вариант), а пятый член -6 (1-й вариант), 20 (2-й вариант).
№2. Найдите сумму первых пяти членов арифметической прогрессии, если её первый член равен -20(1-й вариант), 6 (2-й вариант), а разность равна 10(1-й вариант), -3(2-й вариант).
№3. Найдите сумму первых пяти членов геометрической прогрессии, если её первый член равен 1(1-й вариант), -1 (2-й вариант), а знаменатель равен -2(1-й вариант), 2(2-й вариант).
По окончании диктанта, выборочно, у двоих учеников работы проверяются на оценку, остальные выполняют самопроверку по готовым решениям, записанным на отворотах доски.
Решения:
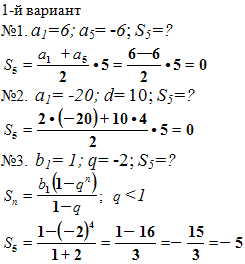
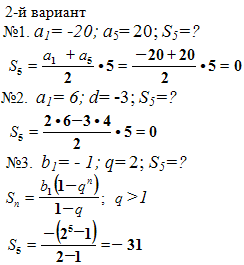
2. Изучение новой темы. (демонстрация презентации. Приложение 1)
1) Слайд №2.
Рассмотрим квадрат со стороной, равной 1. Нарисуем ещё один квадрат, сторона которого равна половине первого квадрата, затем ещё один, сторона которого – половина второго, потом следующий и т.д. Каждый раз сторона нового квадрата равна половине предыдущего.
В результате, мы получили последовательность сторон квадратов
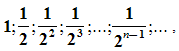 образующих
геометрическую прогрессию со знаменателем
образующих
геометрическую прогрессию со знаменателем
![]() .
.
И, что очень важно, чем больше мы будем строить таких квадратов, тем меньше будет сторона квадрата. Например,
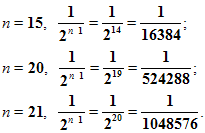
Т.е. с возрастанием номера n члены прогрессии приближаются к нулю.
С помощью этого рисунка можно рассмотреть и ещё одну последовательность. Например, последовательность площадей квадратов:
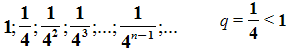 .
И, опять, если n неограниченно возрастает, то площадь, как угодно близко
приближается к нулю.
.
И, опять, если n неограниченно возрастает, то площадь, как угодно близко
приближается к нулю.
2) Слайд №3.
Рассмотрим ещё один пример. Равносторонний треугольник со стороной равной 1см. Построим следующий треугольник с вершинами в серединах сторон 1-го треугольника, по теореме о средней линии треугольника – сторона 2-го равна половине стороны первого, сторона 3-го – половине стороны 2-го и т.д. Опять получаем последовательность длин сторон треугольников.
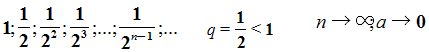
Если рассмотреть геометрическую прогрессию с отрицательным знаменателем.
![]()
То, опять, с возрастанием номера n члены прогрессии приближаются к нулю.
Обратим внимание на знаменатели этих последовательностей. Везде знаменатели были меньше 1 по модулю.
Можно сделать вывод: геометрическая прогрессия будет бесконечно убывающей, если модуль её знаменателя меньше 1.
Фронтальная работа.
Записать определение: геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше единицы.
С помощью определения можно решить вопрос о том, является ли геометрическая прогрессия бесконечно убывающей или нет.
Задача №1.
Является ли последовательность бесконечно убывающей геометрической прогрессией, если она заданна формулой:
а)![]()
Решение:
а) (фронтальная работа, запись на доске)
![]()
![]() данная геометрическая прогрессия является бесконечно убывающей.
данная геометрическая прогрессия является бесконечно убывающей.
б) (самостоятельно)
![]() данная
последовательность не является бесконечно убывающей геометрической прогрессией.
данная
последовательность не является бесконечно убывающей геометрической прогрессией.
Продолжить работу с презентацией.
3) Слайд №4.
Рассмотрим квадрат со стороной, равной 1. Разделим его пополам, одну из половинок ещё пополам и т.д. площади всех полученных прямоугольников при этом образуют бесконечно убывающую геометрическую прогрессию:
![]()
Сумма площадей всех полученных таким образом прямоугольников будет равна площади 1-го квадрата и равна 1.
![]()
Но в левой части этого равенства – сумма бесконечного числа слагаемых.
Рассмотрим сумму n первых слагаемых.![]()
По формуле суммы n первых членов геометрической прогрессии, она равна
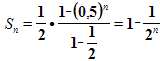 .
.
Если n неограниченно возрастает, то
![]()
4) Слайд №5.
Записать определение. Суммой бесконечно убывающей геометрической
прогрессии называют число, к которому стремится сумма её первых n членов при
n →![]() .
Теперь получим формулу, с помощью которой будем вычислять сумму бесконечно
убывающей геометрической прогрессии.
.
Теперь получим формулу, с помощью которой будем вычислять сумму бесконечно
убывающей геометрической прогрессии.
Рассмотрим формулу n первых членов геометрической прогрессии.
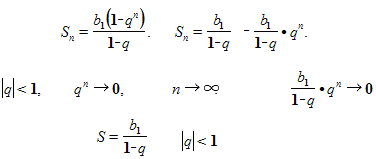
Тренировочные упражнения.
Задача №2. Найти сумму бесконечно убывающей геометрической прогрессии с первым членом 3,вторым 0,3.
Решение:
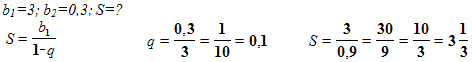
Задача №3. учебник [1], стр. 160, №433(1)
Найти сумму бесконечно убывающей геометрической прогрессии:
![]()
Решение:
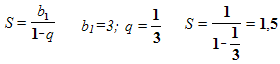
Задача №4. учебник [1], стр. 160, №434(1)
Найти сумму бесконечно убывающей геометрической прогрессии, если
![]()
Решение:
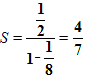
Пользуясь формулой суммы бесконечно убывающей геометрической прогрессии, можно записывать бесконечную периодическую десятичную дробь в виде обыкновенной дроби.
Задача №4. Записать бесконечную периодическую десятичную дробь 0,(5) в виде обыкновенной дроби.
1-й способ. Пусть х=0,(5)= 0,555… /•10 2-й способ. 0,(5)=0,555…=
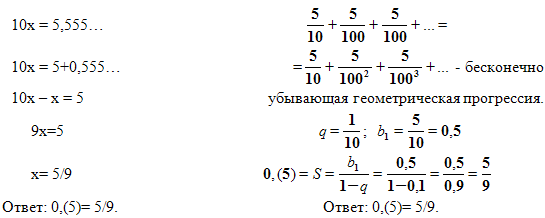
Задача №5. учебник [1], стр. 162, №445(3) (самостоятельное решение)
Записать бесконечную периодическую десятичную дробь 0,(12) в виде обыкновенной дроби.
![]()
Ответ: 0,(12)= 4/33.
5) Слайд №6.
Подведение итогов.
- С какой последовательностью сегодня познакомились?
- Дайте определение бесконечно убывающей геометрической прогрессии.
- Как доказать, что геометрическая прогрессия является бесконечно убывающей?
- Назовите формулу суммы бесконечно убывающей геометрической прогрессии.
Самостоятельная работа. (выполняется в рабочих тетрадях с использованием копирок и чистых листов бумаги, по окончании работы, откопированные записи решений сдаются на проверку, а по записям в тетрадях учащиеся выполняют самопроверку по готовым решениям).
Задания (слайд №6):
- Является ли геометрическая прогрессия бесконечно убывающей, если: b7= -30; b6= 15?
- Найдите сумму бесконечно убывающей геометрической прогрессии: -25; -5; -1;…
- Записать бесконечную десятичную периодическую дробь 0,(9) в виде обыкновенной дроби.
Самопроверка (слайд №7).
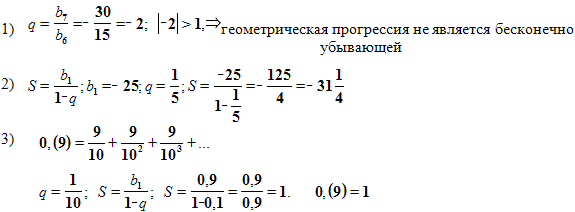
Домашнее задание.
№435(1;3), 445(4), 436. [1]
Литература:
- Алимов Ш.А., Колягин Ю.М., Сидоров и др.- 8-е изд.-М.: Просвещение, 2002.