Цели и задачи:
- изучить мир флексагонов, флексоров и флексманов.
- вызвать интерес к изучению математики.
- способствовать развитию творчества, логического мышления учащихся.
- развивать познавательную деятельность учащихся.
- показать на занятии ряд математических игрушек.
Презентация “Флексагоны, флексоры, флексманы”
Содержание:
Все мы любим занимательную математику. Занимательная математика пробуждает наблюдательность, умение логически мыслить, веру в свои силы. Элемент игры, который делает занимательную математику занимательной, может иметь форму головоломки, состязания, фокуса, парадокса и т.д. Относится ли занимательная математика к чистой или прикладной математике? С одной стороны, занимательную математику, безусловно, следует считать математикой без малейшей примеси утилитарности. С другой стороны, она, несомненно, относится к прикладной математике, ибо отвечает извечной человеческой потребности в игре.
Вероятно, такая потребность в игре лежит в основе даже чистой математики.
Не так уж велико различие между восторгом человека, сумевшего найти ключ к сложной головоломке, и радостью математика, преодолевшего еще одно препятствие на пути к решению сложной научной проблемы. И тот и другой заняты поисками истиной красоты – того ясного, четко определенного, загадочного и восхитительного порядка, что лежит в основе всех явлений. Неудивительно поэтому, что чистую математику порой трудно отличить от занимательной.
Многие считают, что математика не интересна и состоит только из формул, задач, решений и уравнений. Я хочу продемонстрировать своей работой, что математика разноплановая наука, и главная цель – показать, что математика очень удивительный и необычный предмет для изучения.
Я приглашаю на короткую экскурсию в загадочный мир флексагонов, флексоров, флексманов, - бумажных игрушек, обладающих поразительной способностью внезапно менять свою форму и цвет.
1. Флексагоны – это многоугольники, сложенные из полосок бумаги прямоугольной или более сложной формы, которые обладают удивительным свойством: при перегибании флексагонов их наружние поверхности прячутся внутрь, а ранее скрытые поверхности неожиданно выходят наружу. Если бы не одно случайное обстоятельство – различие в формате английских и американских блокнотов, - Флексагоны, возможно, не были бы открыты и по сей день и многие математики лишились бы удовольствия изучать их замысловатую структуру.
Это произошло в конце 1939 года. Как то раз Артур Х. Стоун, 23 летний аспирант из Англии, изучавший математику в Принстоне, обрезал листы американского блокнота, что бы подогнать их под привычный формат. Желая немного развлечся, Стоун принялся складывать из отрезанных полосок бумаги различные фигуры. Одна из сделанных им фигур оказалась особенной интересной. Перегнув полоску бумаги в трех местах и соединив концы, он получил правильный шестиугольник (рис. 1,2), Взяв этот шестиугольник за два смежных треугольника, Стоун подогнул противоположный угол вниз так, что его вершина совпала с центром фигуры. При этом Стоун обратил внимание на то, что когда шестиугольник раскрывался словно бутон, видимой становилась совсем другая поверхность. Если бы обе стороны исходного шестиугольника были бы разного цвета, то после перегибания видимая поверхность изменила бы свою окраску (рис. 3). Так был открыт самый первый флексагон с тремя поверхностями. Поразмыслив над ним ночь, Стоун наутро убедился в правильности своих чисто умозрительных заключений: оказалось, можно построить и более сложный шестиугольник с шестью поверхностями место трех.
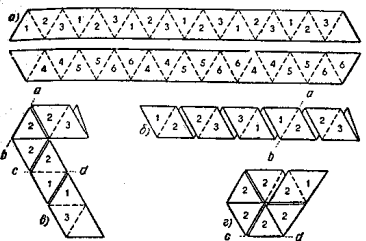
Постоянные модели были названы гексафлексагонами: “гекса” - из-за их шестиугольной формы, “флексагонами” - из-за их способностями складываться. Первый построенный Стоуном флексагон был назван тригексафлексагон, так как у него было три поверхности. Вторая, не менее изящная модель Стоуна получила название гексагексафлексагона (первое “гекса” - шесть – также означает число поверхностей этой модели).
От греческого “гекс”, что означает шесть. To flex (англ.) – складываться, сгибаться, гнуться.1.2 Складывание гексагексафлексагона
Чтобы сложить гексагексафлексагон, берут полоску бумаги, разделенную на девятнадцать равносторонних треугольников. В треугольнике с одной стороны нужно вписать цифры 1, 2, 3. Девятнадцатый (последний) треугольник остается незаполненным. Треугольники на обратной стороне следует пронумеровать цифрами 4, 5, 6. После этого полоску складывают так, чтобы треугольники на ее обратной стороне, имеющие одинаковые цифры, оказались наложенными друг на друга – 4 на 4, 5 на 5, 6 на 6. В результате у нас получится заготовка гексагексафлексагона. Перегнув ее по линиям ab и cd, получим шестиугольник. Остается лишь подвернуть вниз торчащий вправо пустой треугольник и приклеить его к пустому треугольнику на нижней стороне полоски.
Если все сделано верно, то во всех треугольниках на видимой стороне шестиугольника должна стоять цифра 1, а во всех треугольниках на другой стороне – цифра 2. В таком виде гексафлексагон готов к перегибаниям. Взявшись за два смежных трегольника, согнем шестиугольник по общей стороне этих треугольников и подогнем противоположный угол флексагона при этом откроются треугольники с цифрами 3 или 5. Перегибая флексагон наугад, обнаружатся и другие поверхности однако поверхности с цифрами 4, 5 и 6 найти несколько труднее, чем поверхности с цифрами 1, 2 и 3.
Таккерман довольно быстро нашел простейший способ выявления всех поверхностей любого флексагона: держа флексагон за какой либо угол, следует открывать фигуру до тех пор, пока она “открывается”, а затем переходить к следующему углу. Этот метод, известный как “путь Таккермана”, позволяет увидеть все шесть разворотов гексагексафлексагонов за один цикл за двенадцать перегибаний. Поверхности с цифрами 1,2 и 3 будут появлятся в три раза чаще, чем поверхности с цифрами 4,5 и 6. Путь Таккермана удобно изображать в виде схемы. Стрелки указывают в каком порядке становятся видимыми поверхности флексагона. Схемы такого типа пригодны для исследования любой разновидности флексагонов.
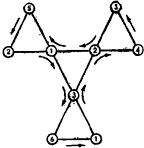
Полная математическая теория флексагонов была разработана в 1940 году Тьюки и Фейнманом. Помимо всего прочего, теория указывает точный способ построения флексагона.
2. Вращающиеся кольца тетраэдров – эта цепочка из тетраэдров обладает удивительной способностью изгибаться и выворачиваться до бесконечности, все время меняя свою форму. Кольцо из тетраэдров – это первый пример флексора – изгибаемого многогранника.
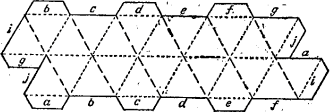
Дж.М. Андреас и Р.М. Сталкер независимо друг от друга открыли семейство изгибаемых конечных многогранников с 2n вершинами, 6n ребрами (из которых 2n сдвоенных) и 4n треугольными гранями; n может равняться 6, 8 или любому большему целому числу. Гранями служат грани n тетраэдров, соединенных между собой в циклическом порядке по определенным парам противоположных ребер каждого, так что получается фигура наподобие кольца. При n = 6 эта фигура еще достаточно жесткая, но при n = 8 она уже может изгибаться и выворачиваться до бесконечности, как колечко дыма. Когда n четно, фигура стремится принять симметричную форму; особенно хороша она при n = 10 (рис. 4). Когда n нечетно, из-за полного отсутствия симметрии картина становится, пожалуй, еще более захватывающей. При n, большем или равном 22, кольцо может заузливаться.
Для изготовления модели кольца достаточно одного листа. В случае n = 6, нужно разместить фигуру, состоящую из 24 правильных треугольников и 9 клапанов. Вырезав ее, нужно сделать сгибы по внутренним линиям – по штриховым линиям вверх, а по пунктирным вниз – и приклейте клапаны в соответствии с буквенными обозначениями.
2.2 Спор о существовании флексора
Кольцо из тетраэдров как изгибаемый многогранник вызывает ряд возражений. Во- первых, в нем есть дырка. Во-вторых, имеются ребра, к которым подходят по четыре грани. Так что непонятно, стоит ли называть это кольцо многогранником.
Чтобы избежать всяких сомнений, при поиске флексоров можно было бы ограничиться только выпуклыми многогранниками, т.е. многогранниками, лежащими по одну сторону от каждой из своих граней. Но имеется знаменитая теорема Коши о том, что любой выпуклый многогранник неизгибаем. Она была доказана в 1813 году. Хотя эта теорема не исключала существования невыпуклых флексоров, но многие математики считали, что и таких флексоров тоже не существует.
2.3 Магическое кольцо из восьми тетраэдров
– является магическим в нескольких смыслах. На нем расположены числа от 1 до 32. Четыре грани каждого тетраэдра дают в сумме 66; соответствующие грани, взятые по одной из каждого тетраэдра дают в сумме 132 (например, 9+7+17+31+10+8+18+32 = 132) – то же самое получается для восьми наборов из восьми граней, которые спирально обвиваются вокруг кольца (например, 1+12+31+21+2+11+32+22 = 132).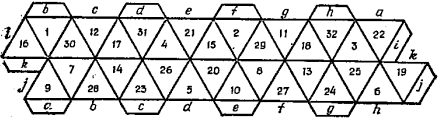
Магическое вращающееся кольцо
3. Флексманы – это существа, населяющие мир флексагонов и флексоров.
Надо вырезать из плотной бумаги квадрат со стороной 15-20 см. Его нужно согнуть по диагоналям сгибом вверх и по штриховой линии сгибом вниз (рис 5). А затем сложить чтобы получился треугольник. Теперь нужно будет проделать четыре одинаковые операции. Результат первой из них – сгиб по штриховой линии рисунка 5, б – изображен на рисунке 5, в, окончательный результат – на рисунке 5, г. Остаются еще четыре одинаковые завершающие операции – отгибание маленьких треугольничков, и перед нами – флексман.
Самое примечательное свойство флексманов – это их умение ходить по наклонным плоскостям. Стоит поставить флексмана на достаточно пологую наклонную плоскость, и он тут же начинает мелкими шажками спускаться по ней. Каждый из флексманов обладает своеобразным характером или, уж во всяком случае, своеобразной походкой.
На следующих занятиях все эти математические фигуры можно с учениками сделать наглядно.
Все эти игрушки приводят ребят в восторг.