Тип урока: урок повторения и закрепления материала.
Цели урока.
Образовательные:
- повторить и закрепить правила, определяющие порядок выполнения действий первой и второй ступени, схему и программу выполнения действий;
- распределительный закон умножения.
Развивающие:
- развитие умений записывать выражения по программе вычислений, выполнять действия по схеме.
- развитие самостоятельности мышления: выражать своё мнение, выделять главное, делать выводы.
- развитие личностного саморазвития учащихся.
- развитие умений и навыков вычислительного характера.
Воспитательные:
- воспитание культуры общения, усидчивости, внимания и трудолюбия.
- формирование самостоятельности и активности, гуманных отношений на уроке.
Оборудование:
МКТ, карточки с заданиями для самостоятельной работы.
Структура урока.
- Организационный момент. (2 мин.)
- Актуализация знаний. (12 мин.)
- Использование знаний в стандартной ситуации. (10 мин.)
- Математический диктант. (5 мин.)
- Самостоятельная работа с последующей проверкой. (12 мин.)
- Постановка домашнего задания. (1 мин.)
- Подведение итогов. (3 мин.)
Ход урока
1. Организационный момент.
Проверяется готовность класса, учащихся к уроку. Учитель отмечает отсутствующих и объявляет цели урока.
2. Актуализация знаний.
Учитель проверяет домашнее задание учащихся. Одного из учеников приглашает к доске для решения № 646 из домашнего задания.
Предполагаемая запись ученика на доске:
Решение:
(1215 + 1387) – 64 • 29 = 746.
- Сложить числа 1215 и 1387.
- Перемножить числа 64 и 29.
- Вычесть из результата команды 1 результат команды 2.
Остальные учащиеся в это время выполняют устные упражнения. (На экране появляются задания с помощью МКТ).
- Вместо квадратиков подставьте такие числа, кроме 1, чтобы равенства оказались верными.
| а) __• х • 7 = 42х | 6 |
| б) __ • 4 • ? в = 60в | 3; 5 |
- Вычислите:
| а) 63 • 49 + 49 • 137 | 9800 |
| б) 348 • 25 – 148 • 25 | 5000 |
Учитель предлагает прокомментировать решения.
Предполагаемые ответы учащихся:
- Выполним умножение чисел 63 и 49.
- Умножим число 49 на 137.
- Результат команды 1 сложим с результатом команды 2.
Учитель.
Все ли согласны с решением?Ученик.
Я не согласен с ней. Можно решить этот пример удобным способом. Для этого применим распределительный закон умножения относительно сложения. Находим сумму чисел 63 и 137, в результате которой, получим круглое число 200 и умножим это число на 49.Получим ответ: 9800. Учитель. Правильно.Аналогично решается задание б).
Учитель дает несколько минут времени для повторения опорных знаний. Учащиеся работают в парах. Затем учитель вызывает к доске двух учеников.
Ученик 1. Какие действия относятся к действиям первой ступени?
Ученик 2. Сложение и вычитание чисел называют действиями первой ступени.
Ученик 1. Какие действия относятся к действиям второй ступени?
Ученик 2. Умножение и деление чисел называют действиями второй ступени.
Ученик 1. В каком порядке выполняют действия , если выражение содержит действия первой и второй ступени и в нем нет скобок?
Ученик 2. Если выражение содержит действия первой и второй ступени, и в нём нет скобок, то сначала выполняют действия второй ступени, а затем – действия первой ступени.
Ученик 1. В каком порядке выполняют действия в выражениях без скобок, если в него входят действия одной и той же ступени?
Ученик 2. Если в выражении нет скобок, и оно содержит действия только одной ступени, то их выполняют слева направо.
Ученик 1. В каком порядке выполняют действия в выражениях, где содержатся скобки?
Ученик 2. Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая при этом правила 1 и 2 ).
Учитель вызывает к доске другую пару.
Как задать программу вычислений выражения: (814 + 36 • 27) : ( 101 – 2052 : 38)?
Запишем следующие команды:
- Перемножим числа 36 и 27.
- Сложим 814 с результатом команды 1.
- Разделим 2052 на 38.
- Вычитаем из 101 результат команды 3.
- Разделим результат команды 2 на результат команды 4.
Учитель предлагает рецензировать ответы учащихся, а затем дает задание одному из учеников для составления схемы вычисления и нахождения значения выражения.
Предполагаемая запись ученика на доске:
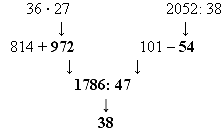
Учитель. Какие выводы можно сделать из ответов учащихся?
Ученик.
Каждое выражение задает программу своего вычисления и эту программу можно изобразить в виде схемы.3. Использование знаний в стандартной ситуации.
Учитель предлагает сначала задания для устного решения по цепочке №№ 634 (в, г), 635, 637, 638 (б, г), а затем дает задание всему классу решить письменно №№ 632(а), 631.
№ 631.
По заданной схеме запишите выражение и выполните действия.
![]()
№ 632 (а).
Составьте схему вычисления и найдите значение выражения.
а) 86 • 12 : 8 + 1414 : 14 = 230.
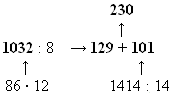
Одновременно у доски двое учащихся выполняют №№ 629, 630.
Физкультминутка.
(Учащиеся с помощью специальных упражнений снимают усталость, набирают силы для дальнейшей работы).Математический диктант.
Запишите числовое выражение и найдите его значение:
- Разность семидесяти и двадцати девяти, увеличенная на одиннадцать.
- Частное шестидесяти и пяти, увеличенное вдвое.
- Из пятидесяти вычесть сумму двадцати четырех и девяти.
- Какое действие выполняется последним при нахождении значения выражения 79 – 27 + 13 – 9 + 11?
- Какое действие выполняется первым при нахождении значения выражения 85 + (42 – 18) – 15?
Верно ли высказывание:
- Сложение и вычитание называют действиями второй ступени.
- В выражении (78 + 94) – 137 скобки можно не писать, так как при этом порядок действий не изменится.
- В выражении (175 – 100) : 25 скобки можно не писать, так как при этом порядок действий не изменится.
IV. Самостоятельная работа с последующей проверкой.
Вариант 1.
Найдите значение выражения, применяя распределительный закон умножения:
| а) 143 • 24 + 24 • 157 | 7200 |
| б) 36 • 248 – 148 • 36 | 3600 |
Решите уравнение:
а) 37у = 444;
б) 300 – 6к = 48;
в) (с – 8) • 12 = 132;
г) 30в – 2в = 532.
Запишите программу вычислений выражения (6944 : 32 – 183) • (79 + 47), составьте схему вычисления и найдите его значение.
Вариант 2.
Найдите значение выражения, применяя распределительный закон умножения:
| а) 746 • 58 – 58 • 546 | 11600 |
| б) 43 • 27 + 35 • 27 – 58 • 27 | 540 |
Решите уравнение:
а) у : 17 = 34;
б) 7с + с – 12 = 28;
в) 243 – (к + 83) = 112;
г) 232: в + 21 = 50.
Запишите программу вычислений выражения (1833: 47 + 467)• 57 - 47• 307, составьте схему вычисления и найдите его значение.
Вариант 3
Найдите значение выражения, применяя распределительный закон умножения:
| а) 367 • 287 + 287 • 133 | 143500 |
| б) 56 • 49 + 227 • 49 – 283 • 49; | 0 |
Решите уравнение:
а) 416 : к + 24 = 50;
б) 42у – 28у + 180 = 600.
Угадайте корень уравнения у + у – 35 = у + 20.
Запишите программу вычислений выражения 378 • 305 – 8208 : (44 • 506 – 22188), составьте схему вычисления и найдите его значение.
Учитель с помощью МКТ высвечивает на экране ответы каждого задания. Учащиеся карандашом исправляют свои ошибки и ставят себе оценку.
V. Постановка домашнего задания.
Учитель. Повторить п.15, решить №№ 644, 647 ( в, г, е ), 649.
Составить кроссворд по теме: “Умножение и деление натуральных чисел” (это задание выполняют только желающие).
Подведение итогов.
Учитель предлагает учащимся оценить ответы тех учеников, которые были самыми активными на уроке. Затем вместе с учащимися подводит итог урока.