Объём призмы. Решение задач
Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать.
Г.Галилей
Цель урока:
- обучить решению задач на вычисление объема призм, обобщить и систематизировать имеющиеся у учащихся сведения о призме и ее элементах, формировать умения решать задачи повышенной сложности;
- развивать логическое мышление, умение самостоятельно работать, навыки взаимоконтроля и самоконтроля, умение говорить и слушать;
- выработать привычку к постоянной занятости, каким- либо полезным делом, воспитание отзывчивости, трудолюбия, аккуратности.
Тип урока: урок применения знаний, умений и навыков.
Оборудование: карточки контроля, медиапроектор, презентация “Урок. Объем Призмы”, компьютеры.
Ход урока
- Организационный момент (2мин.) Цель: формирование мотива, желание работать на уроке.
- Теоретическая разминка (5-6мин.).
Цель: повторение необходимых теоретических сведений по теме, развитие умений говорить и слушать. Работа проходит устно в стационарных парах (совместная работа учащихся сидящих за одной партой, каждый получает возможность говорить, отвечать, проверять, оценивать). Рис.1.
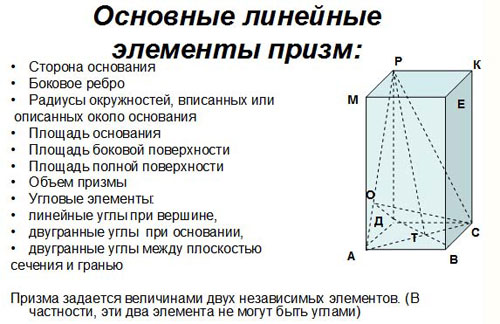
Рис. 1
С помощью рисунка 2, 3, 4, 5 назовите:
- Боковые ребра призмы (рис 2).
- Боковую поверхность призмы (рис 2, рис 5).
- Высоту призмы (рис 3, рис 4).
- Прямую призму (рис 2,3,4).
- Наклонную призму (рис 5).
- Правильную призму (рис 2, рис 3).
- Диагональное сечение призмы (рис 2).
- Диагональ призмы (рис 2).
- Перпендикулярное сечение призмы (ри3, рис4).
- Площадь боковой поверхности призмы.
- Площадь полной поверхности призмы.
- Объем призмы.
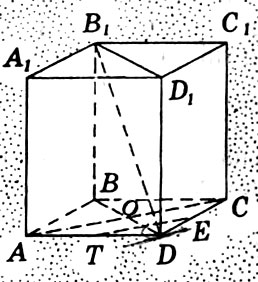
Рис. 2

Рис. 3
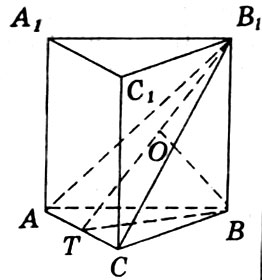
Рис. 4
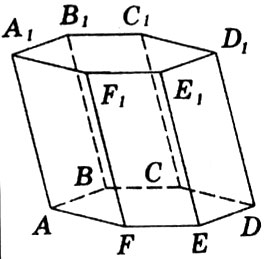
Рис. 5
- ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ (8 мин)
- Совместная работа учителя с классом (2-3мин.).
- ФИЗКУЛЬТМИНУТКА (3 мин)
- РЕШЕНИЕ ЗАДАЧ (10 мин)
- Самостоятельная работа учащихся над тестом за компьютером
- Учитель у доски работает с “сильными” учащимися над решением следующих задач. Задачи комментируются в сопровождении слайдов
- . Постановка домашнего задания. Стр. 67-69, №12, № 15, № 31
- . ПРИЛОЖЕНИЯ ( карточки контроля)
Обменяйтесь тетрадями, проверьте решение на слайдах и выставьте отметку (отметка 10 если составлена задача)
Составьте по рисунку задачу и решите её. Ученик защищает составленную им задачу у доски. Рис 6 и рис 7.
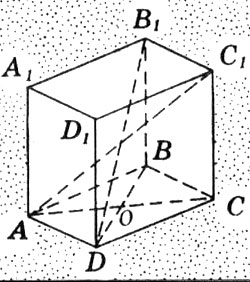
Рис. 6
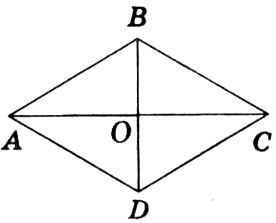
Рис. 7
Глава 2,§3
Задача.2. Длины всех ребер правильной треугольной
призмы равны между собой. Вычислите объем призмы,
если площадь ее поверхности равна ![]() cм2 (рис8)
cм2 (рис8)
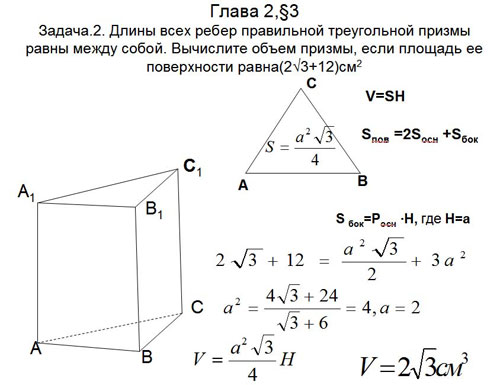
Рис. 8
Глава 2,§3
Задача 5. Основание прямой призмы АВСА 1В 1С1 есть
прямоугольный треугольник АВС (угол АВС=90°),
АВ=4см. Вычислите объем призмы, если радиус
окружности, описанной около треугольника АВС,
равен 2,5см, а высота призмы равна 10см. (рис 9).
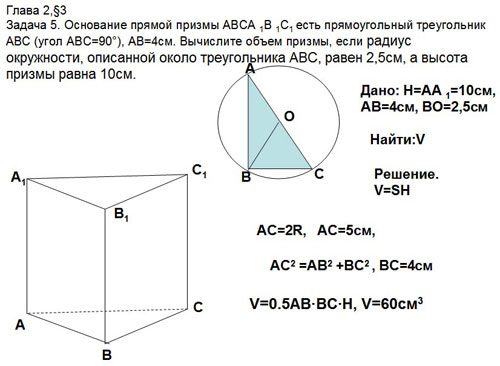
Рис. 9
Глава2,§3
Задача 29.Длина стороны основания правильной
четырехугольной призмы равна 3см. Диагональ
призмы образует с плоскостью боковой грани угол
30°. Вычислить объем призмы (рис 10).
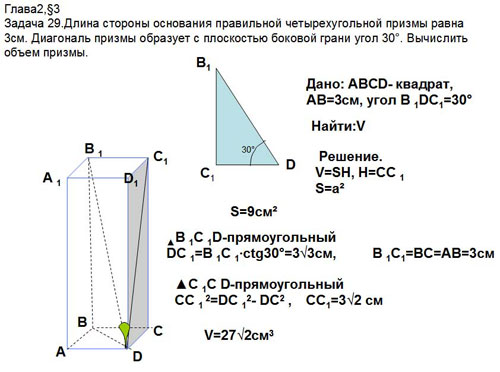
Рис. 10
Цель: подведение итогов теоретической разминки (учащиеся проставляют оценки друг другу), изучение способов решения задач по теме.
На данном этапе учитель организует фронтальную работу по повторению способов решения планиметрических задач, формул планиметрии. Класс делится на две группы, одни решают задачи, другие работают за компьютером. Затем меняются. Учащимся предлагается решить всем № 8 (устно), № 9 (устно). После делятся на группы и преступают к решению задач № 14, № 30, № 32.
Глава 2, §3, страница 66-67
Задача 8. Все ребра правильной треугольной призмы
равны между собой. Найдите объём призмы, если
площадь сечения плоскостью, проходящей через
ребро нижнего основания и середину стороны
верхнего основания, равна ![]() см (рис.11).
см (рис.11).
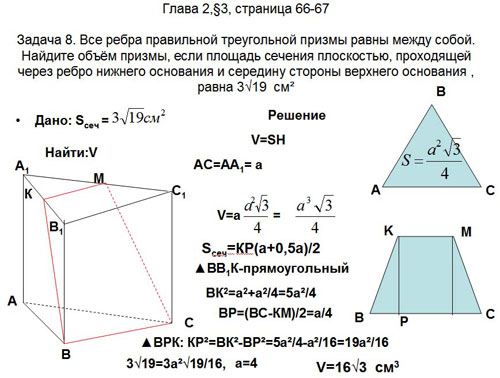
Рис. 11
Глава 2,§3, страница 66-67
Задача 9. основание прямой призмы – квадрат, а ее
боковые ребра в два раза больше стороны
основания. Вычислите объем призмы, если радиус
окружности, описанной около сечения призмы
плоскостью, проходящей через сторону основания и
середину противолежащего бокового ребра, равен ![]() см. (рис.12)
см. (рис.12)
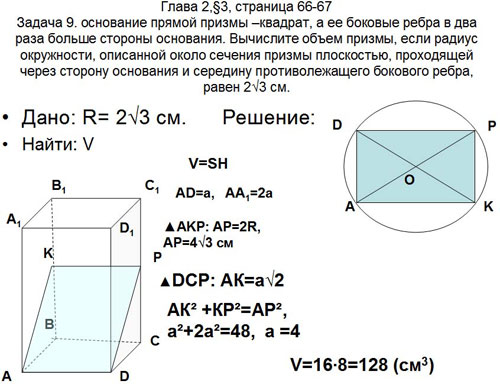
Рис. 12
Глава 2,§3, страница 66-67
Задача 14.Основание прямой призмы – ромб, одна
из диагоналей которого равна его стороне.
Вычислите периметр сечения плоскостью
проходящей через большую диагональ нижнего
основания, если объем призмы равен ![]() и все боковые грани
квадраты (рис.13).
и все боковые грани
квадраты (рис.13).
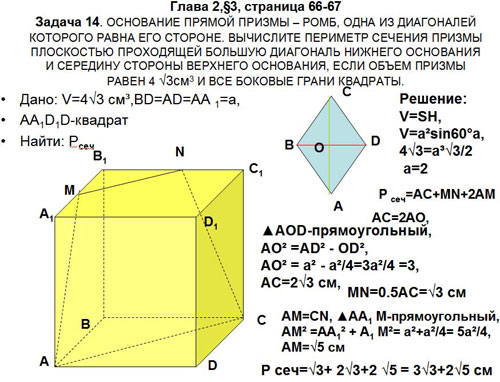
Рис. 13
Глава 2,§3, страница 66-67
Задача 30.АВСА1В1С1
–правильная треугольная призма, все ребра
которой равны между собой, точка о середина ребра
ВВ1. Вычислите радиус окружности, вписанной
в сечение призмы плоскостью АОС, если объем
призмы равен ![]() (рис.14).
(рис.14).
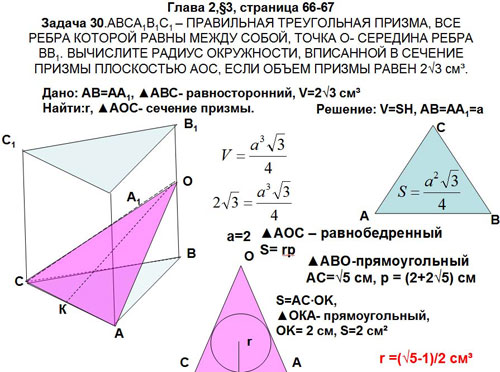
Рис. 14
Глава 2,§3, страница 66-67
Задача 32.В правильной четырех угольной
призме сумма площадей оснований равна площади
боковой поверхности. Вычислите объем призмы,
если диаметр окружности, описанной около сечения
призмы плоскостью, проходящей через две вершины
нижнего основания и противолежащую вершину
верхнего основания, равен 6 см (рис15).
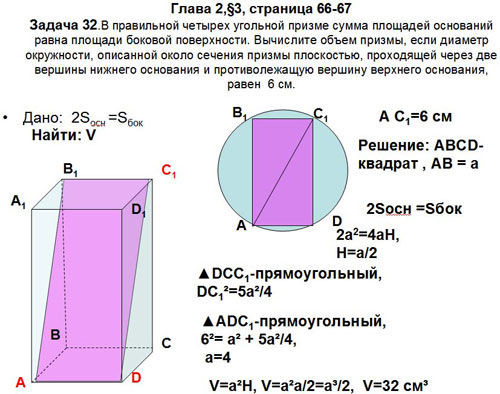
Рис. 15
В ходе решения задач ученики сопоставляют свои ответы с теми, что показывает учитель. Это образец решения задачи с подробными комментариями … Индивидуальная работа учителя с “сильными” учениками (10мин.).
Тест
1. Сторона основания правильной треугольной
призмы равна ![]() , а
высота-5. Найдите объем призмы.
, а
высота-5. Найдите объем призмы.
1) 15![]() 2)45 3)
10
2)45 3)
10![]() 4) 12
4) 12![]() 5)18
5)18![]()
2. Выберите верное утверждение.
1)Объем прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту.
2) Объем правильной треугольной призмы
вычисляется по формулеV=0,25а2h![]() -где а- сторона
основания,h-высота призмы.
-где а- сторона
основания,h-высота призмы.
3)Объем прямой призмы равен половине произведения площади основания на высоту.
4)Объем правильной четырехугольной призмы вычисляется по формуле V=a2h-где а- сторона основания,h-высота призмы.
5)Объем правильной шестиугольной призмы
вычисляется по формуле V=1.5а2h![]() , где а- сторона
основания,h-высота призмы.
, где а- сторона
основания,h-высота призмы.
3.Сторона основания правильной треугольной
призмы равна ![]() .
Через сторону нижнего основания и
противоположную вершину верхнего основания
проведена плоскость, которая проходит под углом
45° к основанию. Найдите объем призмы.
.
Через сторону нижнего основания и
противоположную вершину верхнего основания
проведена плоскость, которая проходит под углом
45° к основанию. Найдите объем призмы.
1) 9![]() 2)9 3)
4,5
2)9 3)
4,5![]() 4) 2,25
4) 2,25![]() 5)1,125
5)1,125![]()
4. Основанием прямой призмы является ромб, сторона которого равна 13, а одна из диогоналей-24. Найдите объем призмы, если диагональ боковой грани равна 14.
1) 720![]() 2) 360
2) 360![]() 3) 180
3) 180![]() 4) 540
4) 540![]() 5)60
5)60![]()
5.Найдите объем правильной шестиугольной
призмы со стороной основания, равной 2, и
высотой,равной ![]() .
.
1) 18![]() 2) 36 3)
9
2) 36 3)
9![]() 4) 18 5)6
4) 18 5)6![]()
Подведение итогов заполнение карточки контроля. (3МИН). Рефлексия (рис.16)

Рис. 16
| Класс Фамилия имя |
Основные Линейные элементы призм: max 8 |
С помощью Рисунка назовите max 8 |
Домашнее задание
max 10 |
Задачи
max 8 |
Тест max10 |
Итоговая Оценка
|
| ТВОЁ ОТНОШЕНИЕ К УРОКУ (ПОДЧЕРКНУТЬ) |
| 1.Отличный, интересный, захватывающий 2. Хороший, содержательный, заставляющий работать 3.Нормальный, обычный 4.Скучный, работа без интереса 5. Бесполезный, совсем не интересный |