Пересечение кривых поверхностей плоскостью и прямой линией

Разделы: Технология

Цели урока:

  1. Рассмотреть вопрос о построении точек, получаемых при пересечении кривых поверхностей плоскостью и прямой линией.
  2. Выявить общий прием решения.
  3. Развитие пространственных представлений и логического мышления.
  4. Формирование графической культуры учащихся.

Ход урока

Пересечение поверхности с плоскостью

При пересечении какой-либо поверхности Ф с плоскость Σ получается некоторого вида плоская фигура, называемая сечением q : q = Ф ∩ Σ.

Если поверхность Ф многогранная, то ее сечение q плоская ломаная линия.

Если поверхность Ф кривая, то ее сечение q плоская кривая, проекции которой строят по отдельным точкам.

Сначала строят опорные точки кривой q:

  • экстремальные точки – самая близкая и самая удаленная относительно плоскостей проекций Π1, Π2, Π3.
  • точки видимости, принадлежащие очерковым линиям поверхности.

Затем дополнительно строят случайные (промежуточные) точки кривой q .

Если секущая плоскость Σ проецирующая, то на той плоскости проекций, которой она перпендикулярна, линия q вырождается в отрезок прямой линии.

Задача 1. Построить сечение пирамиды плоскостью Σ ┴ Π1 (рис.1).

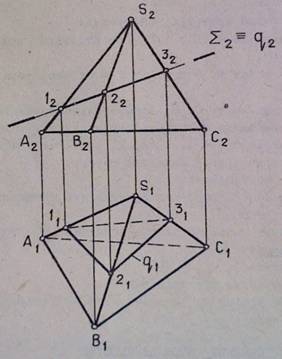
Рисунок 1

Решение. Сечение q – ломаная линия. Ее вершины 1, 2, 3 – точки пересечения ребер пирамиды с плоскостью Σ : 1=SА ∩ Σ, 2= SВ ∩ Σ, 3= SС ∩ Σ ; q2 ≡ Σ2, т.к. Σ ┴ Π2 ; отмечаем точки 12, 22, 32 и строим 11 принадлежащую S1A1, 21 принадлежащую S1В1, 31 принадлежащую S1С1. Соединяем построенные точки с учетом их видимости. Т.к. грань SACотносительно плоскости проекций Π1 невидима, то отрезок 1-3 (11 - 31) тоже невидим.

Задача 2. Построить сечение тора Ф плоскостью Σ ┴ Π2 (рис.2).

Решение. q = Ф ∩ Σ, q – плоская кривая; q2 = Σ 2, т.к. Σ ┴ Π2; q2 – отрезок А2В2, q1– кривая. Строим проекции точек q по их принадлежности соответствующим линиям поверхности тора.

Опорные точки кривой q следующие:

  • высшая точка А принадлежит m, m - фронтальный полумеридиан тора; А2 принадлежит m2, А1 принадлежит m1;
  • низшие точки В, В´ принадлежит a, а – экватор тора;В2, В2´ принадлежат a2, В1, В1´ принадлежат a1;
  • точки видимости С, С´ относительно профильной плоскости проекций Π3. принадлежат профильному меридиану тора. Точки С, С´ и случайные точки 1, 1´, 2, 2´ строятся с помощью параллелей тора, которым принадлежат эти точки.

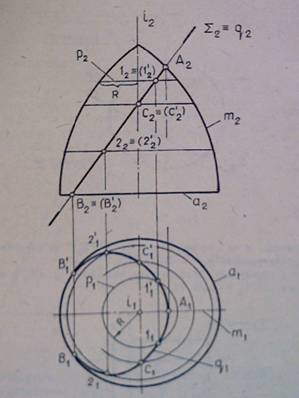
Рисунок 2

Алгоритм построения

1. Через 12, 22 провести фронтальную проекцию p2 параллели p: I2, I2´ принадлежат p2;

2. Построить горизонтальную проекцию p1 параллели p: окружность радиуса R;

3. Построить I1, I1´ принадлежат p1.

Остальные точки строятся так же.

Все точки кривой q относительно Π1 видимые.

Линии видимости относительно Π2 – m(m1).

Сечение цилиндра вращения плоскостью

В сечении могут быть получены следующие линии:

  1. Окружность, если секущая плоскость Г (Г2) ┴ оси i(i2).
  2. Эллипс, если секущая плоскость Σ (Σ2) не параллельна и не перпендикулярна оси i(i2).
  3. Две образующие, если секущая плоскость θ (θ2) параллельна оси i(i2) (рис.3).

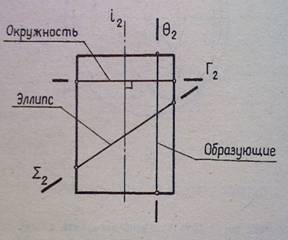
    Рисунок 3

    Сечение сферы плоскостью

    В сечении всегда получается окружность (рис.4).

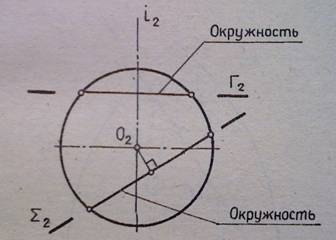
    Рисунок 4

    Сечение конуса вращения плоскостью

    В сечении могут быть получены все виды плоских алгебраических кривых второго порядка:

    1. Эллипс, если секущая плоскость Σ (Σ2) не параллельна ни одной образующей конуса. В частном случае вместо эллипса в сечении получится окружность: Г (Г2) ┴ i (i2) (рис.5);

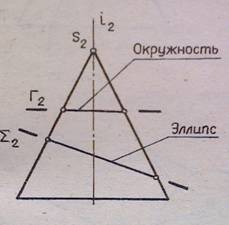
      Рисунок 5

    2. Парабола, если секущая плоскость Σ (Σ2) параллельна одной образующей конуса (рис.6);

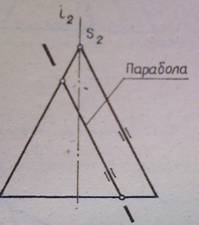
      Рисунок 6

    3. Гипербола, если секущая плоскость Σ (Σ2) параллельна двум образующим конуса (рис.7)

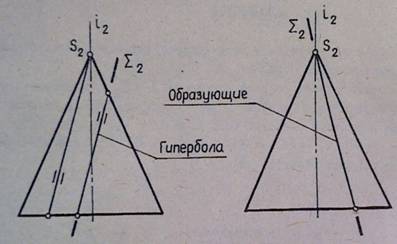
      Рисунок 7

      или две образующие, если секущая плоскость Σ (Σ2) проходит через вершину S(S2) конуса (рис.8).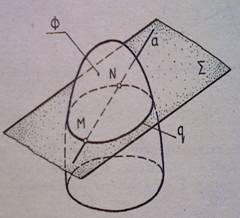

      Рисунок 8

    Пересечение прямой с поверхностью

    В пространстве даны прямая a и поверхность Ф. Определить точки M и N пересечения прямой a и поверхности Ф: M,N = a∩Ф (рис.9). M и N – общие точки прямой a и поверхности Ф, т.е. M и N принадлежат прямой a , M и N принадлежат Ф. Если M и N принадлежат поверхности Ф, то они принадлежат какой-либо линии q, принадлежащей этой поверхности.

    Рисунок 9

    Линия q может быть получена как линия пересечения поверхности Ф и вспомогательной плоскости Σ, проведенной через прямую a : q = Ф∩ Σ.

    Точки M и N принадлежат и прямой a, и линии q, т.е. являются точками их взаимного пересечения: M, N = a∩ q.

    Вспомогательную плоскость Σ через прямую a проводят так, чтобы она пересекала поверхность Ф, по возможности, по графически простой линии q, проекциями которой были тоже графически простые линии.

    В общем случае q плоская кривая. Для построения ее проекций определяют некоторое количество точек – опорных и случайных (см. задачу 2, рис.2).

    Алгоритм решения задачи

    1. Через прямую a провести вспомогательную плоскость Σ ;
    2. Построить линию q пересечения поверхности Ф и вспомогательной плоскости Σ: q = Ф∩ Σ.;
    3. Определить точки M и N пересечения прямой a с построенной линии q: M , N = a∩ q.

    Задача. Определить точки пересечения прямой a и поверхностью тора Ф.

    Решение дано на комплексном чертеже (рис.10):

    1. Через прямую a ( a1,a2) провести вспомогательную фронтально проецирующую плоскость Σ: . Σ ┴ Π2, Σ2 ≡ q2
    2. Построить линию q (q1,q2) пересечения поверхности тора Ф с плоскостью Σ (Σ2); : q = Ф∩ Σ, q – плоская кривая. Т.к. Σ ┴ Π2, то q2 ≡ Σ2; кривая q1 строится по точкам (см. задачу 2, рис.2).
    3. Определить точки M и N пересечения прямой a и построенной линии q: M, N = a∩q; M1, N1 = a1∩q1; M2, N2 = a2∩q2, M(M1, M2) и N(N1, N2) – искомые точки.

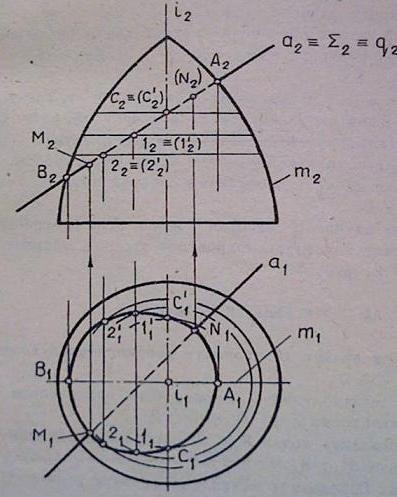
    Рисунок 10

    Следует отметить, что для решения задачи на пересечение прямой с плоскостью общего положения и с поверхностью (рис.9, 10) используется один и тот же алгоритм.