Тип урока: обобщение и систематизация знаний.
Цель урока: систематизировать знания и умения учащихся по темам: «Вписанные и описанные многоугольники. Правильные многоугольники. Длина окружности. Площадь круга.» Выработать у учащихся навыки работы с различными видами тестов.
Методы обучения: словесные, наглядные.
Оборудование:
- Тесты.
- Таблицы для устного счета.
- Справочники по геометрии.
- Л.С. Атанасян, учебник геометрии для 7–9 классов.
- Инструменты.
- Компьютер.
- Презентация (приложение).
Ход урока
I. Организационный момент.
Цель нашего урока - научиться применять полученные знания при выполнении упражнений различного типа. Научиться выполнять тестовые задания, с целью подготовки к ЕГЭ в 9, 11 классах.
II. Актуализация знаний учащихся (повторение теоретического материала):
- Что необходимо знать для построения окружности?
- Охарактеризуйте вписанные и описанные окружности, запишите коротко то, что вы знаете об этих окружностях?
(На доску вывесить таблицы или использовать слайды 1 -8 из презентации, учащиеся проверяют свои записи)
Таблица 1. (Слайды 4,5) Описанная окружность.
- Центр - точка пересечения серединных перпендикуляров.
- Радиус - расстояние от центра до вершины.
- Вершины - лежат на окружности.
Таблица 2. (слайды 6,7) Вписанная окружность.
- Центр - точка пересечения биссектрис.
- Радиус - перпендикуляр к стороне.
- Стороны - касательные.
- Кто не справился с заданием, повторяют п.74, 75 , стр.174, 175.
- Мы повторили вписанные и описанные треугольники.
- А что мы знаем о вписанных и описанных многоугольниках?
а) Вокруг любого многоугольника можно описать окружность?
б) В любой многоугольник можно вписать окружность?
III. Работа с тестами:
1. Математический диктант с (самопроверкой, т. е. проверяются ответы сразу после выполнения заданий): Учитель формулирует условие, учащимся необходимо продолжить предложение.
а) Если стороны многоугольника являются хордами, то окружность называется…(описанной).
б) Если стороны многоугольника являются касательными к окружности, то многоугольник называется…(описанным).
в) Если сторона правильного многоугольника стягивает дугу окружности, равную 72°, то многоугольник имеет …(5) сторон.
г) Сторона правильного треугольника, вписанного в окружность
радиуса R, вычисляется по формуле а3 = … (R![]() ).
).
д) Если диаметр круга равен 4см, то его площадь равна … (S = 4п см2).
2. Установите, истинны или ложны высказывания: (учитель формулирует условие, учащимся необходимо поставить знаки «+» или «-» при выборе ответа)
(За доской работают 4 человека, остальные учащиеся работают в тетрадях)
а) Любой треугольник является правильным, если все его углы равны.(+)
б) Около любого правильного многоугольника можно описать окружность и притом только одну. (+)
в) Окружность, касающаяся всех сторон многоугольника, называется вписанной. (+)
г) Если все вершины многоугольника лежат на окружности, то окружность называется описанной. (+)
д) Многоугольник является правильным, если все его углы равны. (-).
е) Окружность, вписанная в правильный многоугольник, касается каждой стороны многоугольника в его середине. (+).
ж) Сторона правильного треугольника, вписанного в окружность, выражается через радиус этой окружности по формуле а = R ![]() . (+)
. (+)
з) Длину окружности можно вычислить по формуле С = пD, где D - диаметр окружности. (+).
и) Площадь круга равна произведению квадрата его радиуса на п. (+).
(Обратить внимание на задание ж). Выяснить правильность записи. В каком случае надо писать R, в каком r ?).
3. Работа по готовым чертежам.
а) Дан правильный треугольник. Введите обозначения и выразите сторону этого треугольника через радиус вписанной и описанной окружностей. (Слайд 9)
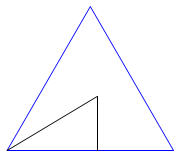
Как называются окружности с общим центром?
Найдите длины окружностей.
Найдите отношение длин окружностей.
б) Решаем у доски: найти отношение площадей круга, вписанного в квадрат и описанного около квадрата. (Слайд 10)
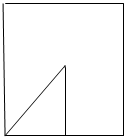
в) Найти зависимость между длиной окружности и площадью круга, ограниченного этой окружностью:
** Дано: С.
Найти: S
** Дано: S
Найти: С.
4. Тесты с выбором ответа (текст распечатан на каждый стол). (Или слайды 11,12)
(За доской работают 4 человека)
а) Чему равна дуга окружности (в градусах), стягиваемая стороной правильного треугольника?
А) 60°; Б) 120°; В) не знаю.
б) Сколько сторон имеет правильный многоугольник, у которого сумма всех углов равна 540°?
А) 5; Б) 6; В) не знаю.
в) Чему равна длина окружности, если ее диаметр равен 50 см?
А) 50 п см; Б)25 п см; В) не знаю.
г) Из круга, радиус которого равен 20 см, вырезан сектор. Дуга сектора равна 90°. Чему равна площадь оставшейся части круга?
А) 100 п см2 ; Б) 300 п см2 ; В) не знаю.
Все задачи, которые мы решили, относятся к группе простых задач. На уроке мы рассмотрели различные виды тестов.
На экзаменах в 9 (пробном) и 11 классах задачи такого типа даются в задании части А, т.е. более легкие задачи. Для получения оценок «4» и «5», необходимо выполнить более сложные задачи, т. е. задачи частей
В (записать ответ, не требуется подробное решение) и задания С (с подробным оформлением решения).
Давайте перейдем к более сложным заданиям.
5. Решение более сложных задач.
а) задачи части В (чертежи заранее заготовлены на доске или на бумаге или из презентации слайды 13–16):
* Дан прямоугольный треугольник, катеты которого равны 3 см и 4 см. Найти длину окружности и площадь круга, вписанного в этот треугольник.
** Периметр правильного треугольника, вписанного в окружность, равен 18 см. Найдите периметр квадрата, вписанного в эту же окружность.
* Сторона правильного треугольника, вписанного в окружность, равна 10. Найдите длину этой окружности.
*** Сторона правильного вписанного шестиугольника равна 12 см. Найдите площадь описанного около этой окружности квадрата.
(Задачи необходимо решать у доски с подробным оформлением), в более сильных классах можно подобрать другие задачи).
(Около правильного шестиугольника описана окружность и в него вписана окружность. Длина большей окружности равна 4п. Найдите площадь кольца и площадь шестиугольника).
IV. Подведение итогов урока. Учитель отмечает, в какой мере достигнуты цели урока, оценивает работу каждого ученика.
V. Задание на дом: № 1117 (а), 1104 (б).