Цели:
- формирование и развитие мыслительных операций (сравнения, абстрагирования, обобщения, конкретизации); форм мышления; умозаключений;
- - развивать познавательный интерес, интерес к творчеству, развивать умения применять знания в незнакомых ситуациях; прививать
- самостоятельность и любознательность;
- - развивать навыки устной и письменной речи, умение четко и ясно задавать вопросы; вычислительные навыки учащихся;
- - развивать у учащихся аккуратность оформления записей, интерес и любовь к предмету.
“Без уравнений нет математики как
средства познания природы…”
П.С.Александров
Тип урока: повторительно-обобщающий
Структура урока:
- Организационный момент
- Устная работа
- Решение уравнений и задач на составление уравнений
- Самостоятельная работа
- Подведение итогов урока
- Определение домашнего задания.
Ход урока
1. Организационный момент. (Определение темы, целей и задач урока, плана работы на урок). На доске тема урока. Запишем число и тему урока в тетрадях.
Перед тем, как начать урок, совершим путешествие в историю математики.
В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники, посвященные в тайные знания, жрецы довольно успешно справлялись с такими задачами.

Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов.
Еще за 3-4 тысячи лет до н.э. египтяне и вавилоняне умели решать простейшие уравнения, вид которых и приемы решения были не похожи на современные. Греки унаследовали знания египтян, и пошли дальше. Наибольших успехов в развитии учения об уравнениях достиг греческий ученый Диофант (III век), о котором писали:
Он уйму всяких разрешил проблем.
И запахи предсказывал, и ливни.
Поистине, его познанья дивны.
Однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IХ века Мухаммеда бен Муссы аль-Хорезми. Слово “аль-джебр” из арабского названия этого трактата – “Китаб аль-джебр валь-мукабела” (“Книга о восстановлении и противопоставлении)- со временем превратилось в хорошо знакомое всем слово “алгебра”, а само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.
В дальнейшем многие математики занимались проблемами уравнений.
Одним из них был французский математик, имя которого вы узнаете, если правильно выполните задания, предложенные для устной работы.
2. Устная работа.
Укажите букву, под которой записано уравнение:
А). 147+25=272; Б). 428-х; В). 404:а-36=8; Г). 417+(15-у); Д). 78х+115.
(правильный ответ под буквой В, на доске выписывается буква В)
Расстояние СD=S(км), скорость велосипедиста 10км/ч. Найдите время движения:
| 10·S (ч); | ||||
| (М) | (А) | (И) |
(на доске выписывается следующий правильный ответ под буквой И).
Из трех чисел 4![]() =К; 0,3=Ю;
=К; 0,3=Ю; ![]() =Е выберите одно, которое надо
поместить в пустой кружок.
=Е выберите одно, которое надо
поместить в пустой кружок.
(правильный ответ выписывается на доску Е)
Решите уравнение:
35:х-20=15
| m= 1; | m= 7; | m=231/3 | ||
| (Т) | (Л) | (Н) |
(правильный ответ выписывается на доску – Т)
Итак, вы узнали имя – ВИЕТ.
Франсуа Виет (1540-1603) родился в городке Фонтене-ле-Конт недалеко от знаменитой крепости Ла-Рошель.Сын прокурора, Виет получил юридическое образование и начал адвокатскую практику в родном городе.
Вскоре Виет переехал в Париж, где он стал советником парламента в Бретани. Знакомство с Генрихом Наваррским, будущим королем Франции Генрихом I?, помогло Виету занять видную придворную должность - тайного советника – сначала при короле Генрихе III, а затем при Генрихе I?. Одним из самых замечательных достижений Виета на королевской службе была разгадка шифра, в котором насчитывалось более 500 знаков, менявшихся время от времени. Этим шифром пользовались недруги французского короля в Нидерландах для переписки с испанским двором. Хотя французы часто перехватывали письма из Испании, расшифровать их никто не мог. И только Виет быстро нашел ключ. Позже испанцы обвиняли Генриха I? в том, что у него на службе состоит дьявол.
Прочитайте выражение:
а) (44-х)-5; б) 17·(у+43); в) 410+(52-m); г) (21-n)·(44+у).
На этом устный счет завершим и перейдем к теме урока:
3.“Решение уравнений и задач на составление уравнений”
№1. Ледокол три дня пробивался через ледяное
поле. В первый день прошел ![]() всего пути, во второй день – 0,6
оставшегося пути, а в третий день – остальные 24
км. Найти длину пути, пройденного ледоколом за
три дня.
всего пути, во второй день – 0,6
оставшегося пути, а в третий день – остальные 24
км. Найти длину пути, пройденного ледоколом за
три дня.

Решение:
| Длина всего пути |
Первый день | Второй день | Третий день |
| х (км) | (x - |
24 км |
Составим и решим уравнение:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ: длина всего пути равна 120 километров.
№2.В трех гаражах 460 машин. Число машин в первом гараже составляет 75% числа машин во втором гараже, а в третьем гараже в 1,5 раза больше машин, чем в первом. Сколько машин помещается в каждом гараже?

Решение:
75% =![]() ;
;
| Первый гараж | Второй гараж | Третий гараж | Всего машин в трех гаражах |
Составим и решим уравнение:
![]()
![]()
![]()
![]()
![]()
Во втором гараже -160 машин.
В первом гараже : 160·![]() = 120 машин.
= 120 машин.
В третьем гараже : 460 – (160+120)=180 (машин).
Ответ: в 1-ом гараже 120 машин; во 2-ом гараже 160 машин; в 3-ем гараже 180 машин.
№3. Разность двух чисел равна 15. Две трети большего из этих чисел и пять шестых меньшего равны 1. Найти эти числа.
Решение:
Пусть первое число х, тогда второе число (х-15).
Две трети большего числа будет ![]() ·х, а пять шестых второго
числа будет
·х, а пять шестых второго
числа будет ![]() (х-15).
Сумма получившихся чисел равна 1. Составим и
решим уравнение.
(х-15).
Сумма получившихся чисел равна 1. Составим и
решим уравнение.
![]()
![]()
![]()
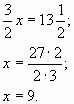
Первое число равно 9, тогда второе число 9-15=-6.
Ответ: 1 число 9, 2-ое число -6.
№4.Решить уравнение:
а) ![]() ; б)
; б) ![]() ; в) (х+1)(х-3)=(х-2)(х-5).
; в) (х+1)(х-3)=(х-2)(х-5).
Решение:
а).![]() б).
б). ![]() в).
в).![]() х2+х-3х-3=х2-2х-5х+10;
х2+х-3х-3=х2-2х-5х+10;
![]()
![]() -2х+7х=10+3;
-2х+7х=10+3;
![]()
![]() 5х=13;
5х=13;
![]()
![]() х=2,6.
х=2,6.
Ответ: а) -![]() ;
б) -
;
б) -![]() или -0,75; в)
2,6.
или -0,75; в)
2,6.
№5. Решите уравнение:
¦![]() ¦ =
¦ =![]() .
.
Решение:
| 1) |
2) |
|
Сделать проверку.
4. Самостоятельная работа (10 мин)
| 1 вариант | 2 вариант | |
| №1.Решите задачу с помощью уравнения | ||
| Три класса школьников сажали деревья. Первый
класс посадил 0,35 всех деревьев,второй класс - |
Из резервуара с керосином отлили сначала 40%,
потом |
|
| №2.Решите уравнение: | ||
| 4·(4+5х)- 5·(1-2х)=-1 | 2·(4-3х)+3·(х-2)=3. | |
Сбор тетрадей для проверки. Анализ самостоятельной работы: |
||
| 1. Ответ: 1000 деревьев. | 1.Ответ: 40 тонн. | |
| 2. х= - |
2.х= |
|
5. Подведение итогов урока.
6. Домашнее задание
№1. Сумма трех чисел равна 1. Третье число на ![]() меньше первого. Второе
число в 2 раза меньше суммы первого и третьего
меньше первого. Второе
число в 2 раза меньше суммы первого и третьего
№2. Решите уравнения:
а). ¦![]() ¦=
¦=![]() б).
б). ![]() в).
в). ![]()
№3. Лыжники маршрут протяженностью в 105 км
прошли за три дня. Во второй день прошли![]() расстояния,
оставшегося после первого дня пути, а в третий
день на 5 км меньше, чем в первый день. Найти
протяженность пути за каждый день.
расстояния,
оставшегося после первого дня пути, а в третий
день на 5 км меньше, чем в первый день. Найти
протяженность пути за каждый день.
Литература
- С.А.Пономарев, П.В.Стратилатов, Н.И.Сырнев. Сборник задач по математике для 5-6 классов. М., Просвещение, 1979.
- Энциклопедия для детей. Аванта +. Математика, т.11. Мю, Аванта +, 2001.