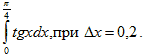Учебно-воспитательные задачи:
- Дидактическая цель. Познакомить учащихся с методами приближённого вычисления определённого интеграла.
- Воспитательная цель. Тема данного занятия имеет большое практическое и воспитательное значение. Наиболее просто к идее численного интегрирования можно подойти, опираясь на определение определённого интеграла как предела интегральных сумм. Например, если взять какое-либо достаточно мелкое разбиение отрезка [a; b] и построить для него интегральную сумму, то её значение можно приближённо принять за значение соответствующего интеграла. При этом важно быстро и правильно производить вычисления с привлечением вычислительной техники.
Основные знания и умения. Иметь понятие о приближённых методах вычисления определённого интеграла по формулам прямоугольников и трапеций.
Обеспечение занятия
- Раздаточный материал. Карточки-задания для самостоятельной работы.
- ТСО. Мультипроектор, ПК, ноутбуки.
- Оснащение ТСО. Презентации: “Геометрический смысл производной”, “Метод прямоугольников”, “Метод трапеций”. (Презентации можно взять у автора).
- Вычислительные средства: ПК, микрокалькуляторы.
- Методические рекомендации
Вид занятия. Интегрированное практическое.
Мотивация познавательной деятельности учащихся. Очень часто приходится
вычислять определённые интегралы, для которых невозможно найти первообразную. В
этом случае применяют приближённые методы вычисления определённых интегралов.
Иногда приближённый метод применяют и для “берущихся” интегралов, если
вычисление по формуле Ньютона-Лейбница не рационально. Идея приближённого
вычисления интеграла заключается в том, что кривая
![]() заменяется
новой, достаточно “близкой” к ней кривой. В зависимости от выбора новой кривой
можно использовать ту или иную приближённую формулу интегрирования.
заменяется
новой, достаточно “близкой” к ней кривой. В зависимости от выбора новой кривой
можно использовать ту или иную приближённую формулу интегрирования.
Последовательность занятия.
- Формула прямоугольников.
- Формула трапеций.
- Решение упражнений.
План занятия
- Повторение опорных знаний учащихся.
Повторить с учащимися: основные формулы интегрирования, сущность изученных методов интегрирования, геометрический смысл определённого интеграла.
- Выполнение практической работы.
Решение многих технических задач сводится к вычислению определённых интегралов, точное выражение которых сложно, требует длительных вычислений и не всегда оправдано практически. Здесь бывает вполне достаточно их приближённого значения.
Пусть, например, необходимо вычислить площадь, ограниченную линией, уравнение которой неизвестно. В этом случае можно заменить данную линию более простой, уравнение которой известно. Площадь полученной таким образом криволинейной трапеции принимается за приближённое значение искомого интеграла.
Простейшим приближённым методом является метод прямоугольников. Геометрически
идея способа вычисления определённого интеграла по формуле прямоугольников
состоит в том, что площадь криволинейной трапеции АВСD заменяется суммой
площадей прямоугольников, одна сторона которых равна
![]() , а друга -
, а друга -
![]() .
.
Если суммировать площади прямоугольников, которые показывают площадь криволинейной трапеции с недостатком [Рисунок1], то получим формулу:
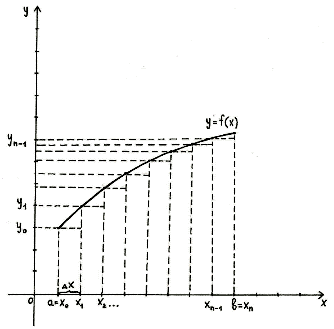
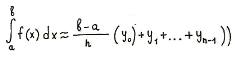
[Рисунок1]
то получим формулу:
![]()
Если с избытком
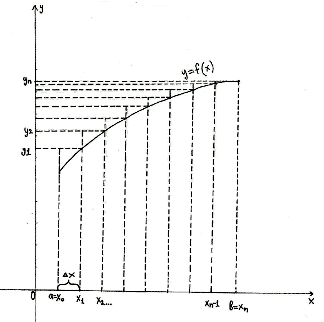
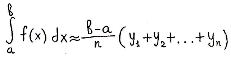
[Рисунок2],
то ![]()
Значения у0, у1,..., уn находят из
равенств ![]() ,
к
=
0, 1...,
n
.Эти
формулы называются формулами прямоугольников и дают приближённый
результат. С увеличением n результат становится более точным.
,
к
=
0, 1...,
n
.Эти
формулы называются формулами прямоугольников и дают приближённый
результат. С увеличением n результат становится более точным.
Итак, чтобы найти приближённое значение интеграла
![]() , нужно:
, нужно:
- разделить отрезок интегрирования [a, b] на n равных частей точками х0= а, х1, х2,..., х n -1, х n = b ;
- вычислить значения подынтегральной функции
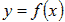 в
точках деления, т.е. найти
у
0
=
f (x0),
у
1
=
f (x1),
у
2
=
f (x2),
у
n
-1
=
f (xn-1),
у
n
=
f (xn)
;
в
точках деления, т.е. найти
у
0
=
f (x0),
у
1
=
f (x1),
у
2
=
f (x2),
у
n
-1
=
f (xn-1),
у
n
=
f (xn)
; - воспользоваться одной из приближённых формул.
Для того, чтобы найти погрешность вычислений, надо воспользоваться формулами:
![]()
![]()
Пример 1. Вычислить по формуле прямоугольников
![]() . Найти
абсолютную и относительную погрешности вычислений.
. Найти
абсолютную и относительную погрешности вычислений.
Решение:
Разобьём отрезок [a, b] на несколько (например, на 6) равных
частей. Тогда а
=
0,
b =
3
,
![]()
х
k = a + k
![]()
![]() х
х
х0 = 2 + 0
![]()
![]() = 2
= 2
х1 = 2 + 1
![]()
![]() = 2,5
= 2,5
х2 = 2 + 2
![]()
![]() =3
=3
х3 = 2 + 3
![]()
![]() = 3
= 3
х4 = 2 + 4
![]()
![]() = 4
= 4
х5 = 2 + 5
![]()
![]() = 4,5
= 4,5
f (x0) = 22 = 4
f
(x
1
)
= 2
,5
2
=
6,25
f
(x
2
)
=
32
=
9
f
(x
3
)
=
3,52
=
12,25
f
(x
4
)
=
42
=
16
f
(x
5
)
=
4,52
=
20,25.
| х | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 |
| у | 4 | 6,25 | 9 | 12,25 | 16 | 20,25 |
По формуле (1):
![]()
Для того, чтобы вычислить относительную погрешность вычислений, надо найти точное значение интеграла:
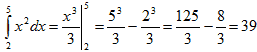
![]()
![]()
Вычисления проходили долго и мы получили довольно-таки грубое округление. Чтобы вычислить этот интеграл с меньшим приближением, можно воспользоваться техническими возможностями компьютера.
Для нахождения определённого интеграла методом прямоугольников необходимо
ввести значения подынтегральной функции f(x) в рабочую таблицу Excel в
диапазоне х ![]() [2
;5
]
с заданным шагом
[2
;5
]
с заданным шагом
![]() х = 0,1.
х = 0,1.
- Открываем чистый рабочий лист.
- Составляем таблицу данных (х и f(x)). Пусть первый столбец будет значениями х, а второй соответствующими показателями f(x). Для этого в ячейку А1 вводим слово Аргумент, а в ячейку В1 – слово Функция. В ячейку А2 вводится первое значение аргумента – левая граница диапазона (2). В ячейку А3 вводится второе значение аргумента – левая граница диапазона плюс шаг построения (2,1). Затем, выделив блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А32, до значения х=5).
- Далее вводим значения подынтегральной функции. В ячейку В2 необходимо
записать её уравнение. Для этого табличный курсор необходимо установить в
ячейку В2 и с клавиатуры ввести формулу =А2^2 (при английской
раскладке клавиатуры). Нажимаем клавишу Enter. В ячейке В2 появляется
4. Теперь необходимо скопировать функцию из ячейки В2.
Автозаполнением копируем эту формулу в диапазон В2:В32.
В результате должна быть получена таблица данных для нахождения интеграла. - Теперь в ячейке В33 может быть найдено приближённое значение интеграла. Для этого в ячейку В33 вводим формулу = 0,1*, затем вызываем Мастер функций (нажатием на панели инструментов кнопки Вставка функции (f(x)). В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле Категория выбираем Математические. Справа в поле Функция - функцию Сумм. Нажимаем кнопку ОК. Появляется диалоговое окно Сумм. В рабочее поле мышью вводим диапазон суммирования В2:В31. Нажимаем кнопку ОК. В ячейке В33 появляется приближённое значение искомого интеграла с недостатком (37,955) .
Сравнивая полученное приближённое значение с истинным значением интеграла (39), можно видеть, что ошибка приближения метода прямоугольников в данном случае равна
![]() =
|39 - 37
,
955| = 1
,045
=
|39 - 37
,
955| = 1
,045
![]()
Пример 2. Используя метод прямоугольников, вычислить
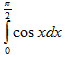 с
заданным шагом
с
заданным шагом ![]() х =
0,05.
х =
0,05.
Решение:
- Для нахождения определённого интеграла значения подынтегральной функции
f(x) должны быть введены в рабочую таблицу Excel в диапазоне
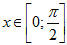 с
заданным шагом
с
заданным шагом 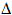 х
= 0,05. В созданную уже таблицу данных в ячейку А2 вводится левая граница
интегрирования (0). В ячейку А3 вводится второе значение аргумента –
левая граница диапазона плюс шаг построения (0,05). Затем, выделив
блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый
нижний угол блока протягиваем до ячейки А33, до значения х=1,55).
х
= 0,05. В созданную уже таблицу данных в ячейку А2 вводится левая граница
интегрирования (0). В ячейку А3 вводится второе значение аргумента –
левая граница диапазона плюс шаг построения (0,05). Затем, выделив
блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый
нижний угол блока протягиваем до ячейки А33, до значения х=1,55).
- Далее вводим значения подынтегральной функции. В ячейку В2 необходимо записать её уравнение. Для этого табличный курсор необходимо установить в ячейку В2. Здесь должно оказаться значение косинуса, соответствующее значению аргумента в ячейке А2. Для получения значения косинуса воспользуемся специальной функцией: нажимаем на панели инструментов кнопку Вставка функции ( f х ) . В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле Категория выбираем Математические. Справа в поле Функция - функцию COS. Нажимаем кнопку ОК. Появляется диалоговое окно COS. Наведя указатель мыши на серое поле окна, при нажатой левой кнопке сдвигаем поле вправо, чтобы открыть столбец данных (А). Указываем значение аргумента косинуса щелчком мыши на ячейке А2. Нажимаем кнопку ОК. В ячейке В2 появляется 1. Теперь необходимо скопировать функцию из ячейки В2. Автозаполнением копируем эту формулу в диапазон В2:В33. В результате должна быть получена таблица данных для нахождения интеграла.
- Теперь в ячейке В34 может быть найдено приближённое значение интеграла. Для этого в ячейку В34 вводим формулу = 0,05*, затем вызываем Мастер функций (нажатием на панели инструментов кнопки Вставка функции ( ( f х )) . В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле Категория выбираем Математические. Справа в поле Функция - функцию Сумм. Нажимаем кнопку ОК. Появляется диалоговое окно Сумм. В рабочее поле мышью вводим диапазон суммирования В2:В32. Нажимаем кнопку ОК. В ячейке В34 появляется приближённое значение искомого интеграла с избытком (1,024056).
Сравнивая полученное приближённое значение с истинным значением интеграла
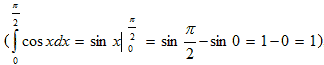 , можно
видеть, что ошибка приближения метода прямоугольников в данном случае равна
, можно
видеть, что ошибка приближения метода прямоугольников в данном случае равна
![]()
![]()
Метод трапеций обычно даёт более точное значение интеграла, чем метод прямоугольников. Криволинейная трапеция заменяется на сумму нескольких трапеций и приближённое значение определённого интеграла находится как сумма площадей трапеций
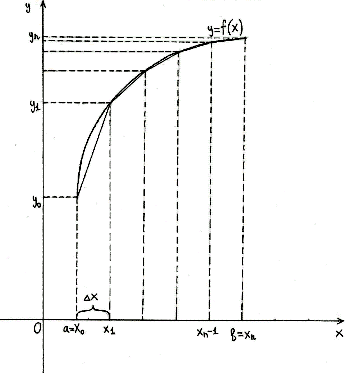
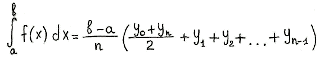
[Рисунок3]
![]()
Пример 3. Методом трапеций найти
![]() с шагом
с шагом
![]() х = 0,1.
х = 0,1.
Решение.
- Открываем чистый рабочий лист.
- Составляем таблицу данных (х и f(x)). Пусть первый столбец будет значениями х, а второй соответствующими показателями f(x). Для этого в ячейку А1 вводим слово Аргумент, а в ячейку В1 – слово Функция. В ячейку А2 вводится первое значение аргумента – левая граница диапазона (0). В ячейку А3 вводится второе значение аргумента – левая граница диапазона плюс шаг построения (0,1). Затем, выделив блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А33, до значения х=3,1).
- Далее вводим значения подынтегральной функции. В ячейку В2 необходимо записать её уравнение (в примере синуса). Для этого табличный курсор необходимо установить в ячейку В2. Здесь должно оказаться значение синуса, соответствующее значению аргумента в ячейке А2. Для получения значения синуса воспользуемся специальной функцией: нажимаем на панели инструментов кнопку Вставка функции f(x). В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле Категория выбираем Математические. Справа в поле Функция - функцию SIN. Нажимаем кнопку ОК. Появляется диалоговое окно SIN. Наведя указатель мыши на серое поле окна, при нажатой левой кнопке сдвигаем поле вправо, чтобы открыть столбец данных (А). Указываем значение аргумента синуса щелчком мыши на ячейке А2. Нажимаем кнопку ОК. В ячейке В2 появляется 0. Теперь необходимо скопировать функцию из ячейки В2. Автозаполнением копируем эту формулу в диапазон В2:В33. В результате должна быть получена таблица данных для нахождения интеграла.
- Теперь в ячейке В34 может быть найдено приближённое значение интеграла по методу трапеций. Для этого в ячейку В34 вводим формулу = 0,1*((В2+В33)/2+, затем вызываем Мастер функций (нажатием на панели инструментов кнопки Вставка функции (f(x)). В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле Категория выбираем Математические. Справа в поле Функция - функцию Сумм. Нажимаем кнопку ОК. Появляется диалоговое окно Сумм. В рабочее поле мышью вводим диапазон суммирования В3:В32. Нажимаем кнопку ОК и ещё раз ОК. В ячейке В34 появляется приближённое значение искомого интеграла с недостатком (1,997) .
Сравнивая полученное приближённое значение с истинным значением интеграла
![]() можно
видеть, что ошибка приближения метода прямоугольников в данном случае вполне
приемлемая для практики.
можно
видеть, что ошибка приближения метода прямоугольников в данном случае вполне
приемлемая для практики.
![]()
![]()
- Решение упражнений.
- Вычислить
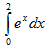 методом прямоугольников, разделив отрезок [0;1] на 20 равных частей.
методом прямоугольников, разделив отрезок [0;1] на 20 равных частей.
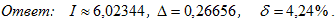
- Вычислить методом трапеций
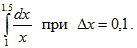
- Вычислить методом трапеций
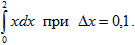
- Вычислить методом трапеций
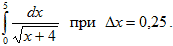
- Вычислить
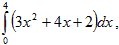 разделив отрезок [0;4] на 40 равных частей.
разделив отрезок [0;4] на 40 равных частей. - Вычислить
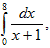 разделив отрезок [0;8] на 40 равных частей.
разделив отрезок [0;8] на 40 равных частей. - Вычислить