Цели:
- Методическая: Повышение активно-познавательной деятельности учащихся путем проведения индивидуально-самостоятельной работы и применения опережающих заданий.
- Обучающая: Повторение определения показательной функции, основные свойства степеней. Ввести понятие логарифма и его свойств. Решение упражнений. Систематизировать знания учащихся по теме; способствовать выработке умений и навыков в вычислении логарифмов, в применении их свойств при логарифмировании и потенцировании; рассмотреть более сложные примеры по теме и проверить навыки и умения при самостоятельном решении упражнений.
- Воспитательная: Воспитание аккуратности, собранности. Проверить сформированность качеств знаний: прочность, глубина, оперативность; формировать гуманные отношения на уроке через работу в парах, умение слушать друг друга; добросовестное отношение к учебному труду, ответственность, честность, сопереживание успехам и неудачам товарищей.
- Развивающая: Развивать интеллектуальные способности, мыслительные процессы, речь, память. Развивать любовь и интерес к математике. Установить, могут ли студенты применять знания логарифмов при решении задач; в ходе урока обеспечить развитие у учащихся самостоятельности мышления и в учебной деятельности;
Тип урока: Комбинированный
Форма проведения урока: Индивидуальная и фронтальная. Решение примеров.
Оборудование: Плакаты на тему “ Показательная функция”, “Логарифмы и его свойства”, “гармошка” с заданиями, таблицы. Карточки-задания для индивидуальной самостоятельной работы, лото-задания, учебная литература.
Эпиграф урока:
“Математику уже затем учить надо, что
она ум в порядок приводит” |
Ход урока
1. Организационный моментВступительное слово преподавателя.
Я приветствую вас на сегодняшнем уроке алгебры. Тема урока: “Логарифм и его свойства”. Сегодня мы повторим понятие логарифма числа, свойства логарифма, закрепим умения применять эти понятия при решении уравнений. Эпиграфом урока являются слова М.В. Ломоносова
“Математику уже затем учить надо, что она ум в порядок приводит”. На доске: дата, тема, план, эпиграф урока.
Объявляется цель и задачи урока. Раздаются тетради для самостоятельных работ и учебники.
2. Актуализация опорных знаний, умений студентов
1. Проверка домашнего задания. №472а), №473а).
(Вызвать 2-х учащихся к доске.)
№ 272а)
>2,5;
> 2,5;
>
;
> 1;
;
Х <0.
Ответ: х ![]()
![]() .
.
№ 273а).
2х
>
; х2 – 3 + 2х > 0; х2 + 2х – 3 > 0.
Решим методом интервалов.
Пусть f (x) = х2 + 2х – 3, где f (x) = 0, т. е. х2 + 2х – 3 = 0.
Д = 22 – 4 * (- 3) = 4 = 12 = 16.
х1 =
х2 =
f (0) = 02 + 2 * 0 – 3 < 0.
Ответ: х ![]() (-
(-![]() ;-3)U(1;+
;-3)U(1;+ ![]() )
)
2. Индивидуальная работа по карточкам (10 мин). (Приложение 1)
(Раздать 6 карточек в виде лото-задания.)
Задания:
- Решить показательные уравнения.
- Решить показательные неравенства.
- Задания на свойства показательной функции.
3. Индивидуальная работа у доски.
(Написать свойства степеней.)
4. Выступление у доски.
(Доклад о происхождении степеней. Сведения из истории) Таблички с именами ученых готовить заранее. (Приложение 2)
5. По стенду дать определение показательной функции, свойства показательной функции.
Далее проверить домашнее задание. (Учащиеся комментирует план выполнения работ.)
Ассистенты самостоятельно проверяют индивидуальные работы учащихся, работающих индивидуально.
6. По “гармошке” решить показательные неравенства и уравнения ( задания готовить заранее.)
3. Формирование новых знаний и понятий
Дата, тема и план урока написать заранее. Эпиграф урока на доске.
Преподаватель: Вы знакомы с шестью действиями над числами
| А+В | А-В | А*В | А/В | А |
Эти действия образуют три пары взаимно
обратных действий. А для того чтобы решить
уравнение а![]() =в
, где а>0 и а
=в
, где а>0 и а ![]() 1 придумали
седьмое действие, которое называется логарифмом.
1 придумали
седьмое действие, которое называется логарифмом.
logа в=с ,где b>0 , а>0, а![]() 1, в=а
1, в=а![]()
Преподаватель:
Совершаем небольшой экскурс в историю математики. Ученики слушают сообщение на тему “Изобретение логарифма”. На доске записи, которые предлагаем записать в тетрадь.
Джон Непер – 1614 год – изобретение логарифма
Бригс – 1624 год – создание таблиц логарифмов.
1703 год – перевод таблиц на русский язык
Л. Магницкий – 1716 год – издание семизначных
логарифмических таблиц.
Логарифмическая линейка
Слово логарифм происходит от греческого (число) и (отношение) и переводится, следовательно, как отношение чисел. Выбор изобретателем (1594 г.) логарифмов Дж. Непером такого названия объясняется тем, что логарифмы возникли при сопоставлении двух чисел, одно из которых является членом арифметической прогрессии, а другое — геометрической.
Определение. Логарифмом положительного числа в при положительном основание а, называется показатель степени, в которую нужно возвести основание а, чтобы получить логарифмируемое число в.
![]()
Формула ![]() (где в>0, а>0 и а
(где в>0, а>0 и а![]() 1 )
называется основным логарифмическим
тождеством.
1 )
называется основным логарифмическим
тождеством.
Пример:
1) log
9=2 т.к. 9>0,3>0, 3=1, 3
=9.
2) log3=0,5 т.к. 3>0, 9>0, 9=1, 9
=3
Преподаватель: Также существуют десятичные и натуральные логарифмы.
Log10 x= lg x –это десятичный логарифм.
Logе x=ln x-это натуральный логарифм.
(Таблички с формулами готовить заранее.)
Логарифмы с основанием е ввел С п е й д е л (1619 г.), составивший первые таблицы для функции In x. Название более позднего происхождения натуральный (естественный) объясняется “естественностью” этого логарифма.
Н. Мерка т о р (1620–1687), предложивший это
название, обнаружил, что In х – это площадь под
гиперболой у = ![]() . Он предлагал также название
“гиперболический”.
. Он предлагал также название
“гиперболический”.
На этом уроке вы познакомитесь со свойствами логарифмов, позволяющими преобразовывать логарифмические выражения, решать логарифмические уравнения и неравенства.
Для этого следует вспомнить свойства степеней.
К доске вызвать учащегося для записи свойств степеней.
Свойство 1. logа x=0
Свойство 2. Logа а=1
Свойство 3. Логарифм произведения положительных чисел равен сумме логарифмов множителей logа xy= logа x+ logв у
Свойство 4. Логарифм частного двух
положительных чисел равен разности логарифмов
делимого и делителя. logа ![]() = logах- logа
у
= logах- logа
у
Свойство 5. Логарифм степени равен
произведению показателя степени на логарифм
основания этой степени. logа x![]() =р logа x
=р logа x
Опережающие задание в виде сообщения о возникновение логарифмов.
(Имена ученых-математиков заранее готовится на плакате) (Приложение 4)
4. Применение знаний, навыков, понятий
Работа учащихся у доски.
(Решение примеров №479 а),б), №480 а),б).)
№479 а),б), №480 а),б).- работать самостоятельно.
№ 479
а) log3
= – 4, так как 3 – 4 = (
)4 =
;
б) log 16 1 = 0. Так как 160 = 1.
№ 480.
а) log5 0,04 = -2, т. к. 5-2 =
=
= 0,04;
б) log7 343 = 3, т. к 73 = 343.
№483 а),б) с объяснением
№ 483.
Найдите логарифмы:
а) log5 25 = 2, т. к. 52 = 25; log5 = -1, т. к. 5-1 =
;
log5 =
, т. к. 5
=
.
б) log8 64 = 2, т. к. 82 = 64; log8 = -1, т. к. 8-1 =
;
log3 2 = , т. к. 8
=
= 2.
№484
а) log3 х = -1; б) log х = -3;
х = 3-1; х = =216; х =
.
№484 а)б), №486 а)б) с объяснением.
№ 486
а) logх 81 = 4; б) logх = 2;
х4 = 81; х2 = ;
х = ;
х = ;
х =3. х = .
Опережающие задание в виде сообщения. Тема “Логарифм и музыка” (Приложение 5)
(Играет музыка )
Преподаватель: Ребята, логарифмы
применяются на уроках физики. Закон
радиоактивного распада имеет вид m=m![]() е
е![]() .Формула Циолковского, связывающая
скорость ракеты с ее массой v=v
.Формула Циолковского, связывающая
скорость ракеты с ее массой v=v![]() ln
ln ![]() .
.
(Все формулы написаны заранее на листе бумаги и прикрепляются на доску с помощью магнитиков.)
№488 – №490 решать устно с места (самостоятельная работа с места по учебнику)
№491 а) Прологарифмируйте по основанию 3 (К доске вызвать учащегося). Решение комментировать.
№ 491а) log3 ![]() =
= ![]() log3
log3 ![]() =
= ![]() log3 а3b =
log3 а3b = ![]() (log3 а3 + log3 b) =
(log3 а3 + log3 b) = ![]() (3log3 а + log3
b) =
(3log3 а + log3
b) = ![]() log3 а
+
log3 а
+ ![]() log3 b.
б) log3
log3 b.
б) log3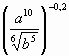 =
log3
=
log3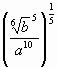 =
= ![]() (log3 b
(log3 b![]() – log3 a10)
=
– log3 a10)
= ![]() log3 b –
log3 b –
![]()
![]() 10 log3 a =
10 log3 a = ![]() log3 b- 2 log3 a.
log3 b- 2 log3 a.
№492 (а, б) Самостоятельно у доски работает учащийся.
№ 492.
а) lg 100![]() = lg 100 +
lg
= lg 100 +
lg ![]() = 2 + lg (ab3c)
= 2 + lg (ab3c)![]() = 2 +
= 2 + ![]() lg ab3c = 2 +
lg ab3c = 2 + ![]() (lg a + 3 lg b + lg c)/
(lg a + 3 lg b + lg c)/
Опережающие задание в виде сообщения. Тема “Звезды, шум и логарифмы” (Приложение 6)
Преподаватель: Более того,
коэффициент звукоизоляции стен измеряется также
с помощью логарифма, по формуле D=A lg![]() .(Приложение
7)
.(Приложение
7)
№495 (а, б) Самостоятельно у доски. (по времени.)
а) lg 8+ lg 125= lg 8*125= lg 1000=3;
б) log2 7- log2
= log2 7/
= log2 16=4
– Давайте, ребята, послушаем еще одно сообщение, которое явно показывает связь математики и физики (Приложение 8)
5. Обобщение и систематизация знаний учащихся1. Словарная работа
– логарифм;
– показательная функция;
– возрастает;
– степень;
– иррациональный показатель;
– тождество.
– экспонента.
2) Эстафета (МАТЕМАТИЧЕСКОЕ ЛОТО.) (Приложение 9)
(заранее готовить 2 варианта заданий.)
6. Итог урокаПодвести итог урока. Сообщить учащимся оценки, отметить наиболее активных..
7. Домашняя работа
№ 479г) -493г) Учить п.37. Готовится к математическому диктанту по пройденной теме.