Цели урока:
- Приблизить знания учащихся 7 класса к стандартам профильного обучения, предусматривающих изучение раздела “Геометрия на плоскости”;
- Рассмотреть замечательные точки и линии треугольника;
- Показать практическое применение этих знаний при решении задач.
Ход урока
1. Оргмомент (5 мин.).
2. Вводное слово учителя:
Геометрия – один из наиболее древних математических наук. Первые геометрические факты мы находим в вавилонских клинописных таблицах и египетских папирусах (III тысячелетие до н.э.), а также в других источниках.
Возникновение геометрических знаний связано с практической деятельностью человека. Так, в Древнем Египте, использовался треугольник со сторонами 5, 4 и 3.

За несколько тысячелетий геометры столь подробно изучили треугольник, что иногда говорят о “геометрии треугольника” как о самостоятельном разделе элементарной геометрии.

Три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке – центре описанной около треугольника окружности (см. рис.1)
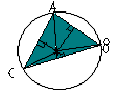
Рис.1
Этот факт следует из свойства серединного перпендикуляра d к отрезку: d состоит из тех, и только тех, точек, которые равноудалены от концов отрезка. Если для треугольника АВС серединные перпендикуляры в АВ и ВС пересекаются в точке О, то IОА I=IОВ I и IОВ I = IОС I, поэтому I ОАI= I ОСI и точка О обязана лежать на серединном перпендикуляре к третьей стороне АС.
2) Биссектрисы трех внутренних углов треугольника пересекаются в одной точке - центре вписанной в треугольник окружности (рис. 2).

Рис.2
Это следует из основного свойства биссектрисы l выпуклого угла: l состоит из тех, и только тех, точек угла, которые равноудалены от его сторон. Если рассмотреть дополнительно биссектрисы трех пар внешних углов треугольника, то получается еще три замечательные точки – центры вневписанных окружностей (рис.3).
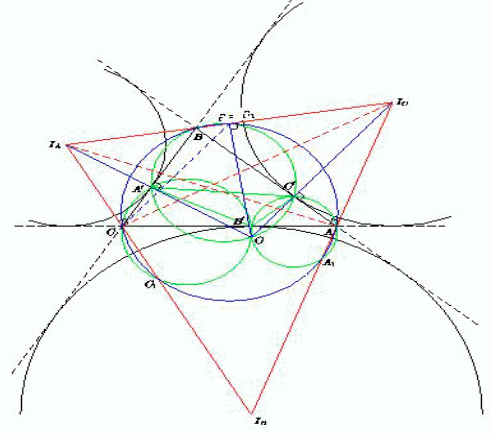
Рис.3
Радиусы описанной, вписанной и вневписанной окружности R, r, ra , rb и rc связаны красивым соотношением
ra+ rb+ rc = r+4R ,
а расстояние между центрами вписанной и описанной окружностей p можно найти по формуле Эйлера:
p2= R2- 2Rr .
Здесь же приведем формулу для площади треугольника:
| S = | abs 4R |
= pr, |
где p- полупериметр треугольника.
3) Все три медианы пересекаются в точке М (рис.4),
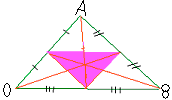
Рис.4
называемой центроидом треугольника АВС (который также является центром масс для тонкой треугольной пластины). Каждая медиана делится точкой М в отношении 2:1, считая от соответствующей вершины треугольника.
4) Высоты треугольника (или их продолжения) также пересекаются в одной точке Н – ортоцентре треугольника (рис.5).
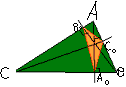
Рис.5.
Пусть высоты треугольника АВС пересекают соответственные стороны (или их продолжения) в точках А0, В0, С0 (рис.6). Треугольник А0В0С0 называется ортоцентрическим для треугольника АВС или, коротко, его ортотреугольником. Оказывается, высоты треугольника являются биссектрисами его ортотреугольника. Если треугольник АВС остроугольный, то ортортреугольник А0В0С0 вписан в треугольник АВС: вершины А0В0С0 лежат на соответствующих сторонах треугольника АВС.
Справедлива замечательная теорема: среди всех треугольников, вписанных в остроугольный треугольник, ортотреугольник имеет наименьший периметр.
5) Теоремы о пересечении высот, медиан, биссектрис треугольника в действительности можно получить из общей “теоремы Чевы” (Д. Чева – итальянский математик, (1648-1734)): отрезки AQ, BR, CP, соединяющие вершины треугольника АВС с точками на противолежащих сторонах (рис.6),
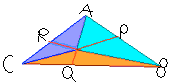
Рис.6
пересекаются в одной точке D тогда, и только тогда, когда AP* BQ* CR = PB* QC *RA.
3. Решение задач на доске учащимися:

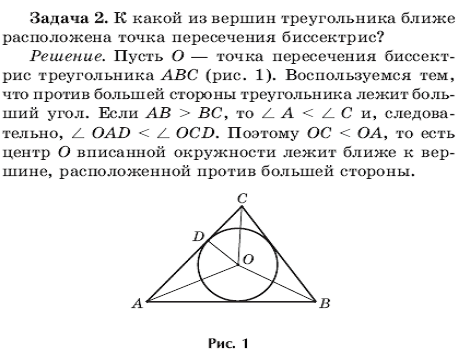
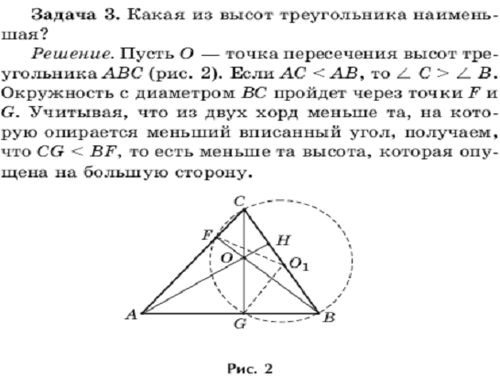
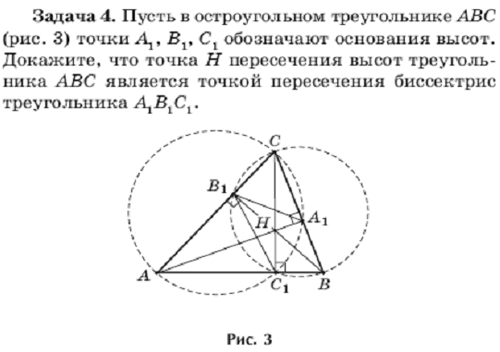






4. Подведение итогов:
- Выставляются оценки выступавшим ученикам;
- Учитель делает выводы по прошедшему уроку.
Литература:
- Энциклопедический словарь юного математика для среднего и старшего школьного возраста. 2-е издание, исправленное и дополненное. Издательство “Педагогика” 1989г.
- Лекции 1-4 “Геометрия на профильном уровне обучения” авторы: И.М.Смирнова, В.А. Смирнов.