В базисном учебном плане астрономия отсутствует, но олимпиаду по этому предмету рекомендовано проводить. В нашем городе Прокопьевске текст олимпиадных задач для 10 - 11 классов составил Евгений Михайлович Раводин заслуженный учитель РФ.
Для повышения интереса к предмету астрономии задания предложены первого и второго уровня сложности.
Приводим текст и решение некоторых заданий.
10 класс
Задача 1. С какой по величине и направлению скоростью должен лететь из Новокузнецкого аэропорта самолет, чтобы, двигаясь вдоль параллели 54°с.ш, прибыть в пункт назначения в тот же час по местному времени, что и при вылете из Новокузнецка?
Задача 2.Диск Луны виден у горизонта в виде полукруга, выпуклостью вправо. В какую сторону мы смотрим, приблизительно в котором часу, если наблюдение происходит 21 сентября? Ответ обосновать.
Задача 3. Что такое "астрономический посох", для чего он предназначен и как устроен?
Задача 4. Можно ли наблюдать Луну за сутки до солнечного затмения? А за сутки до лунного? Ответ обосновать.
Задача 5. Можно ли в школьный телескоп с диаметром объектива 10 см наблюдать космический аппарат размером 2 м, опускающийся на Луну?
11 класс
Задача 1. Звездная величина Веги 0,14. Во сколько раз эта звезда ярче Солнца, если расстояние до нее 8,1 парсек?
Задача 2. В давние времена, когда солнечные затмения "объясняли" захватом нашего светила чудовищем, очевидцы находили подтверждение этому в том, что при частном затмении наблюдали под деревьями, в лесу световые блики, "напоминающие форму когтей". Как научно объяснить такое явление?
Задача 3. Во сколько раз диаметр звезды Арктур (![]() Волопаса) больше Солнца, если
светимость Арктура 100, а температура 4500 К?
Волопаса) больше Солнца, если
светимость Арктура 100, а температура 4500 К?
Задача 4. Можно ли наблюдать Луну за сутки до солнечного затмения? А за сутки до лунного? Ответ обосновать.
Задача 5. Звездолет будущего, имея скорость 20 км/с, пролетает на расстоянии 1 пк от спектрально-двойной звезды, у которой период колебаний спектра равен суткам, а большая полуось орбиты составляет 2 астрономические единицы. Сможет ли звездолет вырваться из поля тяготения звезды? Массу Солнца принять за 2*1030 кг.
Решение задач муниципального этапа олимпиады школьников по астрономии
10 класс
Задача 1.
Решение:
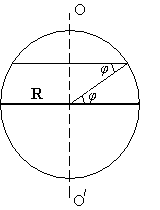
Земля вращается с запада на восток. Время определяется положением Солнца; поэтому чтобы самолет находился в одном и том же положении относительно Солнца он должен лететь против вращения Земли со скоростью равной линейной скорости точек Земли на широте трассы. Данная скорость определяется по формуле:
![]() ; r =
R3 соs?
; r =
R3 соs?

![]()
Ответ: v = 272 м/с = 980 км/ч, лететь на запад.
Задача 2.
Ответ:
Если Луна видна из горизонта, то в принципе её можно видеть либо на западе, либо на востоке. Выпуклость вправо соответствует фазе I четверти, когда Луна отстаёт в суточном движении от Солнца на 900. Если луна у горизонта на западе, то это соответствует полуночи, солнце в нижней кульминации, причём точно на западе это произойдёт в дни равноденствий, следовательно, ответ: смотрим на запад, приблизительно в полночь.
Задача 3.
Ответ:
Древний прибор для определения угловых расстояний на небесной сфере между светилами. Представляет собой линейку, на которой подвижно закреплена траверса, перпендикулярно этой линейки, на концах траверсы укреплены метки. В начале линейки есть визир, сквозь который смотрит наблюдатель. Перемещая траверсу и смотря через визир, он совмещает метки со светилами, между которыми определяют угловые расстояния. На линейке нанесена шкала по которой можно в градусах определить угол между светилами.
Задача 4.
Ответ:
Затмения бывают тогда, когда Солнце, Земля и Луна находятся на одной прямой. Перед солнечным затмением Луна не успеет дойти до линии Земля - Солнце. Но при этом за сутки будет вблизи неё. Эта фаза соответствует новолунию, когда Луна обращена к Земле тёмной стороной, и к тому же теряется в лучах Солнца - поэтому не видна.
За сутки перед лунным затмением Луна не успевает дойти до линии Солнце - Земля. В это время она находится в фазе полнолуния, и поэтому видна.
Задача 5.
Решение:
Телескоп с диаметром D = 0,1 м имеет согласно
формуле Рэлея угловое разрешение ![]() ;
;
![]() 500 нм (зеленый) - длина
волны света (берется длина волны к которой
наиболее чувствителен человеческий глаз)
500 нм (зеленый) - длина
волны света (берется длина волны к которой
наиболее чувствителен человеческий глаз)
![]() = 6,1· 10-6
= 6,1· 10-6
Угловой размер космического аппарата ![]() ;
;
l - размер аппарата, l = 2 м;
R - расстояние от Земли до Луны, R = 384 тыс.км
![]() , что меньше разрешения
телескопа.
, что меньше разрешения
телескопа.
Ответ: нет
11 класс
Задача 1
Решение:
Для решения применим формулу, которая связывает видимую звездную величину m с абсолютной звездной величиной М
М = m + 5 - 5lg D,
где D - расстояние от звезды до Земли в парсеках, D = 8,1 пк;
m - звездная величина, m = 0,14
М- звездная величина, которую наблюдали бы с расстояния данной звезды со стандартного расстояния 10 парсек.
М = 0,14 + 5 - 5lg 8,1 = 0,14 + 5 - 5*0,9 = 0,6
Абсолютная звездная величина связана со светимостью L формулой
lg L = 0,4 (5 - М);
lg L = 0,4 (5 - 0,6) = 1,76;
L = 58
Ответ: в 58 раз ярче Солнца
Задача 2.
Ответ:
Во время частного затмения Солнце наблюдается в виде яркого полумесяца. Промежутки между листьями являются небольшими отверстиями. Они, работая, как отверстия в камере обскуре дают на Земле множественные изображения серпов, которые легко принять за когти.
Задача 3.
Решение:
Воспользуемся формулой ![]() , где
, где
DА - диаметр Арктура по отношению к Солнцу;
L = 100 - светимость Артура;
ТА = 4500 К - температура Арктура;
ТС = 6000 К - температура Солнца
Ответ: DA ![]() 5,6
диаметров Солнца
5,6
диаметров Солнца
Задача 4.
Ответ:
затмения бывают тогда, когда Солнце, Земля и Луна находятся на одной прямой. Перед солнечным затмением Луна не успеет дойти до линии Земля - Солнце. Но при этом за сутки будет вблизи неё. Эта фаза соответствует новолунию, когда луна обращена к земле тёмной стороной, и к тому же теряется в лучах Солнца - поэтому не видна.
За сутки перед лунным затмением Луна не успевает дойти до линии Солнце - Земля. В это время она находится в фазе полнолуния , и поэтому видна.
Задача 5.
Решение:
v2 - ?
v1 = 20 км/с = 2*104 м/с
r = 1 пк = 3*1016 м
А = 2 а.е.
mo = 2*1030 кг
Т = 1 сут = ![]() года
года
G = 6,67*10-11Н*м2/кг2
Найдём сумму масс спектрально-двойных звёзд по
формуле m1 + m2 = ![]() * mo = 1,46*1033 кг
* mo = 1,46*1033 кг
Скорость убегания рассчитаем по формуле второй космической скорости (поскольку расстояние между компонентами спектрально- двойной звезды - 2 а.е. много меньше 1пк)
![]() = 2547,966 м/с =
2,5 км/ч
= 2547,966 м/с =
2,5 км/ч
Ответ: 2,5 км/ч, скорость звездолета больше, поэтому улетит.