Тип урока: урок закрепления знаний.
Цели урока:
- образовательная - совершенствовать навыки действий с рациональными дробями; формировать умения выполнять тождественные преобразования рациональных выражений;
- воспитательная - воспитывать у школьников любознательность, чувство национальной гордости, патриотизма; создание положительного эмоционального фона на уроке;
- развивающая – развивать интерес к математике и её истории, развивать внимание, учить проводить доказательные рассуждения, используя математическую речь; учить умению сосредотачиваться на учебной деятельности и предупреждать ошибки по невнимательности (развивать самоконтроль); развивать творчество учеников.
Этапы урока
1. Организация начала занятия. Сообщение темы и постановка цели.
2. Актуализация опорных знаний учащихся.
3. Закрепление знаний и способов действий.
4. Информация о домашнем задании, инструкция о его выполнении. (вариативное).
5. Подведение итогов урока.
6.Рефлексия.
7. Физкультурная минутка (развитие двигательной сферы, гимнастика для глаз).
Ход урока
1. Организация начала занятия
Сообщение темы и постановка цели. (Слайд № 1)
Если мы откроем Большой Энциклопедический словарь, то сможем прочитать, что обозначает слово «преобразование». Итак, «Преобразование - замена одного математического объекта аналогичным объектом, получаемым из первого по определенным правилам».
В Толковом Словаре Ожегова читаем: «преобразовать - совершенно переделать, превратить из одного вида в другой, из одной формы в другую…, изменить к лучшему».
Объясните мне, пожалуйста, зачем нужна замена одного математического объекта аналогичным ему объектом?
(Выслушиваются ответы детей.)
Т.о. тождественные преобразования алгебраических выражений представляют собой набор методов, позволяющих быстро и легко упростить сложное выражение и привести его к более компактному. Целью тождественных преобразований может быть приведение выражения к виду, более удобному для численных расчетов или дальнейших преобразований.
Итак, сегодня на уроке мы будем совершенствовать навыки действий с рациональными выражениями; формировать умения выполнять их тождественные преобразования.
2. Актуализация опорных знаний учащихся
Ребята, давайте вспомним, какие тождественные преобразования мы знаем.
К тождественным преобразованиям относятся:
- приведение подобных членов;
- раскрытие скобок;
- разложение на множители;
- приведение алгебраических дробей к общему знаменателю.
(На этапе актуализации предложен кроссворд на повторение теоретических фактов, необходимых на уроке.)
У каждого из вас на парте лежит кроссворд. Такой же кроссворд вы видите на экране. Угадав все слова и записав их в клеточки по горизонтали, в выделенном вертикальном столбце вы прочтете одно замечательное слово. (Слайд № 2)
(Разгадав кроссворд, в выделенном вертикальном столбце ученики читают слово «истина»)
Почему мне захотелось выделить это слово? Потому что мы сегодня познакомимся с фрагментами биографии одной известной женщины-математика, у которой девизом всей жизни было: «служить истине, служить справедливости». Но знакомиться мы будем в результате выполнения учебных заданий по теме сегодняшнего урока.
3. Закрепление знаний и способов действий
1) (Слайд № 3)
Кто же эта женщина? Выберите её имя из четырёх имён известных женщин, каждому из которых соответствует набор из единиц и нулей. Правильному ответу на вопрос соответствует набор, имеющий некоторое отличительное свойство по сравнению с другими наборами.
Ответ: С.В.Ковалевская. Набор (10111) отличается от трёх других тем, что состоит из четырёх единиц и нуля, а другие – из трёх единиц и двух нулей. (Слайд № 4)
Отметим кратко, чьи портреты, помимо С.В.Ковалевской, представлены на слайде.
(Справка учителя)
Приложение4
2) (Слайд № 5)
Число, записанное под годом рождения С.В.Ковалевской, равно количеству верных равенств среди следующих:
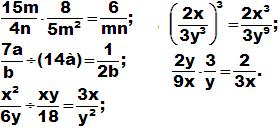
У каждого из вас на партах лежат карточки зелёного и красного цвета. Если вы считаете, что равенство верное, то поднимите карточку зелёного цвета, если – неверное, то красного.
Ответ: Верных равенств четыре, равенство под буквой г) неверное, нарушено правило возведения дроби в степень.
(Слайд № 6)
(Справка учителя)
3) Рассмотрим примеры, включающие в себя все действия с дробями. Порядок их выполнения - такой же, как и с числовыми дробями. Существует два способа записи таких примеров:
1) «цепочкой» - для несложных примеров;
2) по действиям – для более сложных. (Слайд № 7)
Чтобы узнать название имения Крюковских, найдите значение выражения при х = 2, у = 5 и представьте ответ в виде десятичной дроби:
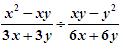
(Один ученик у доски выполняет задание и записывает пример «цепочкой»)
Решение:
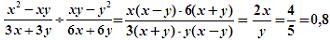
(Справка учителя)
(Слайд № 8)
4) (Слайд № 9)
Чтобы узнать фамилию первого учителя Софьи Ковалевской, упростите выражение.
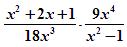
(Один ученик у доски выполняет задание и записывает пример «цепочкой». Остальные выполняют задание самостоятельно с последующей проверкой.)
Решение:
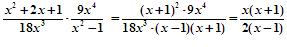
(Справка учителя)
(Слайд № 10)
5) (Слайд № 11)
Чтобы узнать имя петербургского учителя Софьи Ковалевской, упростите выражение и найдите его значение при х = -5 и у = 3.
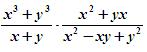
(Самостоятельная работа учащихся с последующей проверкой.)
Ответ: 10
(Слайд № 12)
(Справка учителя)
Физкультурная минутка (развитие двигательной сферы, гимнастика для глаз)
(Слайд № 13)
6) (Слайд № 14)
Сравните значения выражений А и В при р = -3,75, и вы узнаете имя знаменитого немецкого математика, ставшего научным руководителем С. Ковалевской.
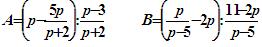
(Учащиеся решают задания по вариантам: 1 вариант находит значение выражения А, 2 вариант – выражения В. Два ученика у доски выполняют задания, записывая решение по действиям. Затем сравнивают получившиеся ответы.)
Ответ: значения выражений А и В равны.
(Справка учителя)
(Слайд № 15)
7) (Слайд № 16)
Знаете ли вы, в каком университете читала лекции и
заведовала кафедрой С.В.Ковалевская?
Чтобы узнать это, решите уравнение:
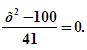
(с комментированием с места).
Ответ: х =10, х = -10.
(Справка учителя).
8) (Слайд № 17)
Подберите числа и запишите их в квадратных скобках так, чтобы получилось тождество. Вы сможете узнать, в какой области С. В. Ковалевская была так же талантлива, как и в математике.
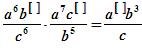
Решение:
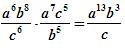
(Справка учителя)
(Слайд № 18)
4. Информация о домашнем (вариативном) задании, инструкция о его выполнении
Даны 3 различных варианта домашнего задания, каждому из вас предлагается решить один из них по выбору (задания имеют «подсказку» - сложность задания).
5. Подведение итогов урока
6. Рефлексия
Перед вами карточка с изображением горы. Если вы считаете, что тема урока была интересна, что хорошо и с пользой потрудились на уроке, узнали что-то новое, то нарисуйте себя на вершине высокой горы. Если осталось что-то неясно, нарисуйте себя ниже.
Хочется закончить наш урок стихами Софьи Ковалевской.
Если ты в жизни, хотя на мгновенье
Истину в сердце своём ощутил,
Если луч правды сквозь мрак и сомненье
Ярким сияньем твой путь озарил:
Чтобы в решеньи своём неизменном
Рок ни назначил тебе впереди -
Память об этом мгновеньи священном
Вечно храни, как святыню, в груди
Тучи сберутся громадой нестройной,
Небо покроется чёрною мглой,
С ясной решимостью, и с верной спокойной
Бурю ты встреть и померься с грозой.
Спасибо за работу!
(Слайд № 19)
К уроку имеется презентация и справка для учителя.