Цели: формирование знаний о возможных вариантах формул для вычисления суммы n первых членов арифметической прогрессии; развитие умений сравнивать, сопоставлять, обобщать, выявлять закономерности; воспитание уважительного отношения к труду как умственному, так и физическому; показ тесной связи математики с физикой, расширение кругозора обучающихся.
Ход урока
1. Фронтальный опрос – подготовка к восприятию нового материала.Что называется числовой последовательностью? Приведите примеры числовых последовательностей.
Какие бывают последовательности? (классификация: конечная, бесконечная, возрастающая, убывающая). Приведите примеры таких последовательностей.
Перечислите способы задания последовательностей. В чём их отличие? Какой из способов наиболее удобен и широко применим и почему?
2. Устная работа.Задание №1.
Дана числовая последовательность (Сn): 17, 14, 11, 8, 5, 2. Дайте полную характеристику этой последовательности (конечная, убывающая,…). Выясните, является ли она арифметической прогрессией и объясните почему? (Да, так как по определению арифметической прогрессии каждый член данной последовательности, начиная со второго, равен предшествующему члену, сложенному с одним и тем же числом -3. Это число – разность арифметической прогрессии.). Задайте эту последовательность тремя способами:
- Рекуррентный: С1=17, Сn+1= Сn–3 – рекуррентная формула.
- Аналитический: Сn=С1–3(n – 1) – формула n – го члена.
- Описательный: пользуясь определением арифметической прогрессии.
Задача. (См. приложение 1, слайд №2) Садовнику нужно изготовить лестницу для сбора яблок из 13 ступеней так, чтобы длина каждой следующей ступени была меньше предыдущей на 2 см. Какой длины брусок нужно взять садовнику для этих перекладин, если первая снизу длиной 50 см?
На слайде №3 демонстрируется садовая лестница.
Создана проблемная ситуация. Обучающиеся понимают, что для ответа на вопрос задачи необходимо найти сумму 13-ти слагаемых, а сначала сами слагаемые: 50, 48, 46, 44, … – последовательность, которая является арифметической прогрессией по определению. Это долго и нерационально. Поэтому надо бы вывести формулу для вычисления суммы n первых членов арифметической прогрессии.
4. Объяснение нового материала.Записываем в тетрадях тему урока: Формула суммы n первых членов арифметической прогрессии.
Каждую ступеньку можно обозначить как члены арифметической прогрессии: а1, а2,…, а13.
Появляется вторая лестница (слайд №4) и
обучающиеся замечают некоторую закономерность:
а![]() +а
+а![]() =а
=а![]() +а
+а![]() =…=а
=…=а![]() +а
+а![]()
Всего 13 пар слагаемых, сумма пар одинакова.
Используя это свойство, найдём сумму длин ступенек 2 лестниц
S = (а![]() + а
+ а![]() )13 и поделим на
2.
)13 и поделим на
2.
![]()
494 см = 4 м 94 см
Ответ: садовнику понадобится брусок длиной 4м 94 см.
Таким образом, задача решена и для любого числа n получена формула
![]()
Её удобно использовать, если известны а1 и
аn. А если известны а1 и d, то лучше
зная, что аn = а![]() + d(n – 1), получить другую формулу
(это могут сделать сами обучающиеся).
+ d(n – 1), получить другую формулу
(это могут сделать сами обучающиеся).
Sn= ![]()
Sn= ![]()
Можно пойти другим путём и оставить вывод второй формулы до решения задачи №1. Тогда перед обучающимися снова будет стоять проблема, и они воочию убедятся в необходимости получения и применения новой формулы. Также полезно предложить обучающимся для использования в решении задач следующие формулы:
![]()
![]()
![]()
Задание №2.
Вычислите длину необходимого садовнику бруска, используя 2-ую формулу.
Вывод: что необходимо знать для вычисления суммы n первых членов арифметической прогрессии?
6. Закрепление изученного материала.№369(б).
Задача №1.
Тело в первую секунду прошло 15 м, а в каждую следующую на 2 м больше, чем в предыдущую. Какой путь прошло тело за 20 с?
Прочитав задачу, обучающиеся понимают, что необходимо вычислить сумму n первых членов арифметической прогрессии, в которой a1 = 15, d = 2, n =20. Решение оформляется следующим образом.
Решение: выбираем удобную формулу и записываем её общий вид:
Sn= ![]()
S20 = ![]() = (30
+ 2
= (30
+ 2![]() = 680
= 680
Ответ: 680 м – путь тела за 20 с.
Задача №2.
Тело падает с башни, высота которой 26 м. Первую секунду оно проходит 2 м, а за каждую следующую секунду – на 3 м больше, чем за предыдущую. Сколько секунд пройдёт до падения тела?
Анализируя условие задачи можно задать 9-тиклассникам вопрос из области физики. Почему тело во время падения за каждую последующую секунду проходит путь больше, чем за предыдущую? Так как они уже знакомы с равноускоренным движением и причиной падения тел на Землю, то могут дать полный ответ на поставленный вопрос. Для активизации внимания обучающихся полезно показать слайд №5, на котором изображена Пизанская башня, можно сказать и несколько слов о ней, дать возможность сделать короткое сообщение кому-то из обучающихся (прямо на уроке спросить, что им известно о ней?).
Решение: Sn =![]()
26 = ![]()
52 = (4 + 3n – 3)n
52 = 3n2 + n
3n2 + n – 52 = 0
D = 625 = 252 > 0 =>2 корня
n1,2 = ![]()
n1 = 4, n2 = – 4![]()
Число секунд не может быть отрицательным числом, значит n = 4.
Ответ: тело упадёт через 4 с.
Задача №3. Том Сойер красил забор длиной 105 м, причем день за днем количество выкрашенного за день уменьшалось на одну и ту же величину. За сколько дней был выкрашен забор, если за первые три дня Том выкрасил 36 м забора, а за последние три дня – 27 м?
Решение:
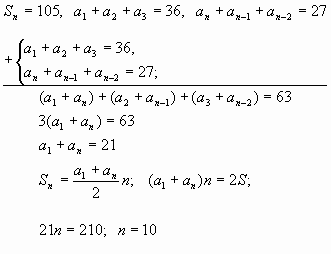
Ответ: 10 дней.
7. Итог урока:а) а1 и аn; б) а1 и d?
8. Домашнее задание:п.15-17
№371а, №373 – объяснить алгоритм выполнения
№386 – на повторение свойств степени.