Формирование у учащихся ключевых компетентностей – одна из основных задач современного образования.
Компетенция – готовность субъекта эффективно соорганизовывать внутренние и внешние ресурсы для постановки и достижения цели.
Внутренние ресурсы: знания, умения, навыки, способы деятельности психологические особенности , ценности и т.д.
Внешние ресурсы: информация, люди, группы, организации и т.д.
Важно отличать ключевые компетентности как результат образования от других результатов образования, в частности, от традиционных знаний, умений и навыков. Принципиальным отличием компетентностей является то, что они как результат образования формируются и проявляются в деятельности. Следовательно, чтобы убедиться, что учащийся освоил тот или иной аспект компетентности на требуемом уровне, следует дать обучаемому задание, выполнить которое можно только осуществив определенную деятельность. Т.е. компетентностный подход – это подход, реализующий деятельностный характер образования.
Как при обучении математики сформировать ключевые компетенции?
Появление нового результата образования поставило учителя перед необходимостью использования деятельностных технологий, методов и приемов работы с учащимся на уроке и во внеурочное время, среди них проблемное и проектное обучение.
Типы проблемных ситуаций, используемых на уроках:
- ситуация неожиданности;
- ситуация конфликта;
- ситуация несоответствия;
- ситуация неопределенности;
- ситуация предположения;
- ситуация выбора.
В своей практике использую исследовательские, творческие, информационные проекты.
Важнейшим видом учебной деятельности при обучении учащихся математике является решение задач. Причем, основное внимание направлено на развитие способности учащихся применять полученные в школе знания и умения в жизненных ситуациях. Но как показывают итоги исследований PISA , выявляются характерные недочеты математической подготовки российских школьников. К ним относятся недостаточное усвоение ряда тем, имеющих широкое практическое применение: отношение чисел, пропорциональные величины, решение задач на проценты, определение периметров и площадей фигур, оценка и прикидка результатов, чтение графиков реальных зависимостей. Именно умение решать большинство из этих практических задач будет проверяется с 2010 года на ЕГЭ.
Поэтому одним из путей формирования ключевых компетентностей является использование на уроках специальных компетентностно-ориентированных задач.
Если на уроках математики систематически использовать компетентностно-ориентированные задачи , то это будет способствовать формированию ключевых компетенций учащихся, повысится математическая грамотность учащихся.
“Под математической грамотностью понимается способность учащихся:
– распознавать проблемы, возникающие в окружающей действительности, которые
могут быть решены средствами математики;
– формулировать эти проблемы на языке математики;
– решать эти проблемы, используя математические знания и методы;
– анализировать использованные методы решения;
– интерпретировать полученные результаты с учетом поставленной проблемы;
– формулировать и записывать окончательные результаты решения поставленной
проблемы”.
На уроках математики необходимо формировать такие компетенции:
- информационная;
- коммуникативная;
- исследовательская;
- готовность к самообразованию.
Для формирования информационной компетентности можно использовать задачи содержащие информацию, представленную в различной форме (таблицах, диаграммах, графиках и т.д.). Вопрос задачи может быть сформулирован следующим образом: переведите в графическую (словесную) форму; если возможно, хотя бы приближенно опишите их математической формулой; сделайте вывод, наблюдается ли в этих данных какая-то закономерность и др.
Примеры:
1) 9-й класс (алгебра) Продолжить числовую последовательность: 1; 3; 5; 7; 9;… задать ее следующими способами:
– Формулой n-го члена;
– Таблицей;
– Графиком;
– Словесным описанием.
Выполнение задания предполагает планирование информационного поиска, извлечение вторичной информации, осуществление первичной обработки информации.
2) 8-й класс (алгебра) Составьте текст задачи, которую можно решить с помощью
данного уравнения, и решите ее:
![]()
Выполнение задания предполагает планирование информационного поиска, извлечение вторичной информации, осуществление вторичной обработки информации
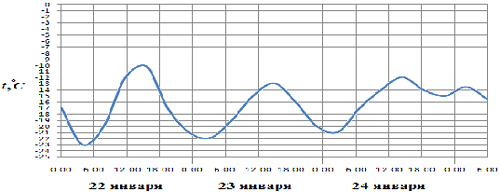
3) 7, 8-й класс (алгебра.) На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали – значение температуры в градусах Цельсия. Определите по рисунку наибольшую температуру воздуха 22 января.
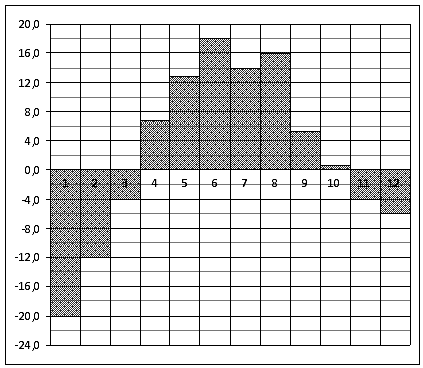
4) На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в 1973 году.
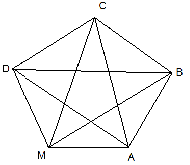
5) 5-й класс (математика). Дана схема дорог между селами A, B, C, D, M и известны расстояния между ними:
AM = 7км, AB = 4км, BC = 9км, CD = 6км, DM = 7км, BM = 5км, BD = 13км, AD = 10км, CM = 11км, AC = 6км. В селе А находится почта. Почтальон должен развозить почту во все села. Необходимо выбрать кратчайший путь для него.
Для формирования коммуникативной компетентности можно использовать групповую форму организации познавательной деятельности учащихся на уроках. Например: Каждой группе предлагается решить задачу предложенным способом и доказать правильность своего решения оставшимся группам.
Примеры:
1) При изучении темы “Применение подобия треугольников” (8-й класс) трем группам предлагается решить задачу одним из способов:
Определить высоту предмета:
а) С помощью вращающейся планки.
б) С помощью тени.
в) С помощью зеркала.
Для формирования исследовательской компетентности учащимся можно предложить задания, в которых необходимо исследовать все возможные варианты и сделать определенный вывод.
1) Телефонная компания предоставляет на выбор три тарифных плана.
| Тарифный план | Абонентская плата | Плата за 1 минуту разговора |
| 1. Повременный | 135 р. в месяц | 0,3 р. |
| 2. Комбинированный | 255 р. за 450 минут в месяц | 0,28 руб. за 1 минуту сверх 450 мин. в месяц. |
| 3. Безлимитный | 380 р. | 0 р. |
Абонент выбрал наиболее дешевый тарифный план, исходя из предположения, что общая длительность телефонных разговоров составляет 650 минут в месяц. Какую сумму он должен заплатить за месяц, если общая длительность разговоров в этом месяце действительно будет равна 650 минут? Ответ дайте в рублях.
2) Строительной фирме нужно приобрести 75 кубометров пенобетона у одного из трех поставщиков. Цены и условия доставки приведены в таблице. Сколько рублей придется заплатить за самую дешевую покупку с доставкой?
| Поставщик | Стоимость пенобетона (руб. за м3) |
Стоимость доставки (руб.) | Дополнительные условия |
| A | 2650 | 4500 | |
| Б | 2700 | 5500 | При заказе на сумму больше 150000 руб. доставка бесплатно |
| В | 2680 | 3500 | При заказе более 80 м3 доставка бесплатно |
Или задачи, в которых необходимо проанализировать предложенную ситуацию, поставить цель, спланировать результат, разработать алгоритм решения задачи, проанализировать результат:
– учебный эксперимент;
– практические работы;
– домашнее задание поисковой направленности;
– интерактивные занятия;
– задачи исследовательского характера.
Для формирования готовности к самообразованию учащимся необходимо предлагать самостоятельно изучить некоторый теоретический материал, составить задачу , формировать умения работать самостоятельно с различными источниками информации, а именно:
– использовать доклады, короткие сообщения учащихся по теме;
– работать со справочниками;
– использовать Интернет-ресурсы;
– подготавливать презентации.
При решении компетентностно-ориентированных задач основное внимание должно уделяться формированию способностей учащихся использовать математические знания в разнообразных ситуациях, требующих для своего решения различных подходов, размышлений и интуиции.
Содержание заданий желательно связывать с традиционными разделами или темами, составляющими основу программ обучения;
Для применения на уроке компетентностно-ориентированных заданий могут быть использованы следующие дополнительные возможности изучаемого материала:
– прикладной характер содержания темы;
– содержание, включающее в себя оценку явлений и событий;
– местный материал;
– содержание программы, связанное с событиями, явлениями, объектами, доступными
непосредственному восприятию школьника (в том числе в учебных ситуациях);
– содержание программы, связанное с формированием учебных умений и навыков;
– содержание учебного материала, которое может найти применение в воспитательной
(внеучебной) деятельности.
Компетентностно-ориентированные задания могут использоваться на уроках различных типов: изучения нового материала, закрепления знаний, комплексного применения знаний, обобщения и систематизации знаний, урок контроля, оценки и коррекции.
На уроках изучения нового материала с помощью компетентностно-ориентированной задачи можно создать условия для формирования понятий, вывода и усвоения формул.
Пример: урок геометрии в 8-м классе по теме “Площади многоугольников”, с использованием проектного метода.
Проблема: необходимо разбить клумбы для цветов около школы в форме параллелограмма, трапеции, треугольника. Сделать необходимые расчеты. Выход на проблему: необходимо знать площади данных фигур.
Работа в группах по выводу формул площади параллелограмма, треугольника, трапеции. При затруднении – обращение к учебнику.
Выполнение расчетов для разбивки клумб, решение практических задач.
Формировать компетентности учеников можно на разных этапах урока
| Этапы урока | Цель Результативность |
Виды деятельности |
| Проверка домашнего задания | Цель: активировать умственную
деятельность учеников, развивать критическое мышление, учить оценивать
знания учеников Результативность: формирование познавательной компетентности |
1. Рецензирование ответов (домашнего задания) |
| Цель: развивать самостоятельность
мышления, формировать гибкость и точность мысли, развивать внимание и
память Результативность: формирование самообразовательной компетентности |
2. Математический диктант, тест, с/р (по страницам домашнего задания с ограничением времени решения) |
|
| Изучение нового материала | Цель: учить исследовательской работе Результативность: формирование исследовательской компетентности |
Доказательство теорем Вывод формул, правил |
| Цель: учить краткой рациональной записи,
отрабатывать умение делать выводы и обобщения Результативность: формирование информационной компетентности |
Проблемная лекция с использованием приобретенной учениками информации | |
| Цель: учить оперировать знаниями,
развивать гибкость использования знаний Результативность: формирование исследовательской, самообразовательной, компетентностей |
Экспериментальная работа Практическая работа |
|
| Закрепление, тренировка, отрабатывание умений и навыков | Цель: изучить свойства, правила…
Результативность: формирование познавательной компетентности |
С/ р частично-поискового, исследовательского характера; Компетентностно-ориентированные задания |
| Цель: закрепить знания; разработать
правила (алгоритмы) запоминания Результативность: формирование компетентности саморазвития |
Исследование различных видов памяти | |
| Цель: закрепить умение решать задачи и
примеры, формировать умения проверять, слушать, думать Результативность: формирование познавательной компетентности |
Решение задач, примеров с комментированием, индивидуальная работа с самопроверкой, игровые формы, КСО | |
| Цель: развивать личную позицию учеников,
опираясь на их знание темы Результативность: формирование интеллектуально– познавательной компетентности |
Решение задач несколькими способами | |
| Цель: обучать работе с информацией;
закрепить знание текста, понимание темы Результативность: формирование коммуникативной и познавательной компетентностей |
Работа с учебником (учебная практическая работа) |
|
| Творческая работа | Цель: показать на основе изученного
материала умение учеников создавать проекты Результативность: формирование исследовательской компетентности |
Создание проектов |
| Цель: учить учеников на основе своих
знаний находить решения задач прикладного характера Результативность: формирование самообразовательной, информационной, коммуникативной компетентностей |
Компетентностно-ориентированные задания | |
| Контроль | Цель: учить детей воображению и умению
абстрагироваться Результативность: формирование самообразовательной, исследовательской компетентности |
Создание рекламы (презентации) изучаемой темы урока, синквейна, работа в группах со взаимной оценкой |
| Цель: учить детей, опираясь на полученные
знания, самостоятельно работать Результативность: формирование самообразовательной ,социальной компетентности |
Разноуровневая с/р с (взаимопроверка, самопровекрка, контроль учителя); | |
| Домашнее задание | Цель: проверить усвоение материала урока,
формировать умение подбирать примеры Результативность: формирование самообразовательной компетентности |
Составить вопросы, задачи и примеры по теме урока |
| Цель: проверить знания учеников согласно
их уровню подготовки Результативность: формирование интеллектуально– познавательной компетентности |
Разноуровневые задачи; Задачи исследовательского характера Творческие задания |
Таким образом, применение деятельностных форм организации обучения можно считать одним из основных путей формирования ключевых компетентностей учащихся.