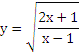Цели:
- обобщение знаний учащихся по данной теме;
- формирование навыков самообразования, самоорганизации работы в группах;
- воспитание навыков общения, умения выслушивать и общаться в группе.
Оборудование и наглядность к уроку: компьютер, мультимедийный проектор, Презентация, таблица, раздаточный материал: «Справочные сведения», план решения заданий.
Подготовительная работа к уроку – семинару:
1. За несколько дней до семинара сообщить план и основные вопросы, выносимые на семинар;
- Историческая справка о развитии числа. Философское учение Пифагора о числе. Выступление учащихся с сообщениями.
- Свойства радикалов; Справочные сведения.
Задание: При каком целом положительном х значение выражения
ближе всего к числу 0,7?
- Справочные сведения об иррациональных уравнениях и способах их решения; Справочные сведения об иррациональных неравенствах и способах их решения.
2. Обсудить с учащимися план их выступления на семинаре.
3. В оказании помощи в подготовке к семинару проводить индивидуальные консультации для учащихся и групп учащихся.
План проведения занятия
1. Вводное слово преподавателя
Когда мы задумываемся о происхождении того или
иного понятия, то для разрешения этого вопроса
чаще всего обращаемся к толковому словарю.
В большом толковом словаре русского языка найдем
определение иррациональности:
С философской точки иррациональность
– недоступность рассудку, то, что не может быть
постигнуто разумом, что явно не подчиняется
законам законом логики и не может быть выражено в
логических понятиях, что оценивается как
«сверхразумное».
С математической точки
иррациональность – несоизмеримость с единицей;
не является ни целой, ни дробной величиной.
Действительно ли понятие иррациональность– это
что-то « уму непостижимое, несоизмеримое,
немыслимое».
На этот вопрос мы и постараемся сегодня найти
ответ в первой на уроке.
Выступление учащихся на семинаре сопровождается
презентацией.
2. Первое выступление учащихся с сообщениямиисторическая справка
Обратимся к истории математики. Когда речь идет
о чем-то очень простом и понятном, мы говорим:
«Дело ясно. Как дважды два – четыре!» А прежде
чем додуматься до того что дважды два четыре,
людям пришлось много учится, много тысяч лет.
Конечно, это учение шло не за партой. Человек
постоянно учился жить: строить жилища,
обрабатывать землю, находить дорогу в дальних
походах. Везде нужны знания математики.
Наглядным пособием для изучения математики были
окружающие предметы. Всякий отдельный предмет:
солнце на безоблачном небе, луна в ясную ночь, сам
человек – вызывали представление о числе «один».
Так глаза, уши, руки человека, крылья птицы
служили представлением о числе «два».
Постепенно, пользуясь сначала пальцами рук. А
потом и пальцами ног, люди удлинили счет. Так в
сознании людей возникло представление о
натуральных числах ![]()
Дополнив натуральные числа нулем и
отрицательными числами, расширили множество
натуральных чисел, до множества целых чисел ![]()
Прошли годы, столетия и в уме человека
зарождается идея о действиях над числами. Так
возникла одна из древнейших наук –
арифметика.
Греческий математик Евклид в 3 веке до н.э. создал
первую математическую школу.
Л.Ф. Магницкий (1703 году) – создал первый учебник
арифметики в России.
В 18 веке Ньютон определил понятие числа как
отношение одной величины к другой, того же рода. С
этого времени в математике определилось понятие
дробного числа.
2000 лет назад знаменитый римский оратор Цицерон
говорил: «Без знания дробей никто не может
признаваться сведущим в арифметике».
R: ![]()
Прошло много времени после открытия дробей, пока человеческий ум обнаружил в процессе измерения величин существования иных чисел, кроме целых и дробных.
3. Выступление «Понятие об иррациональном числе
История иррациональных чисел восходит к удивительному открытию пифагорейцев еще в VI в. до н.э. А началось все с простого, казалось бы, вопроса: каким числом выражается длина квадрата со стороной 1?
Диагональ разбивает квадрат на два одинаковых
прямоугольных треугольника, в каждом она
является гипотенузой. Поэтому, как следует из
теоремы Пифагора, длина диагонали квадрата равна
![]() . Сразу же
возникает соблазн достать микрокалькулятор и
нажать клавишу извлечения квадратного корня. На
табло мы увидим 1,4142135. Более совершенный
калькулятор, выполняющий вычисления с высокой
точностью, покажет 1,414213562373. А с помощью мощного
современного компьютера можно вычислить с
точностью до сотен, тысяч, миллионов знаков после
запятой. Но даже самый высокопроизводительный
компьютер, сколь бы долго он ни работал, никогда
не сможет ни рассчитать все десятичные цифры
числа, ни обнаружить в них какой-либо период.
. Сразу же
возникает соблазн достать микрокалькулятор и
нажать клавишу извлечения квадратного корня. На
табло мы увидим 1,4142135. Более совершенный
калькулятор, выполняющий вычисления с высокой
точностью, покажет 1,414213562373. А с помощью мощного
современного компьютера можно вычислить с
точностью до сотен, тысяч, миллионов знаков после
запятой. Но даже самый высокопроизводительный
компьютер, сколь бы долго он ни работал, никогда
не сможет ни рассчитать все десятичные цифры
числа, ни обнаружить в них какой-либо период.
Для пифагорейцев, положивших в основу своей
философии число как результат измерения и
соотношения между величинами, реальный
прямолинейный отрезок – диагональ квадрата со
стороной равной единице – лишен числового
образа, т. е. такого отрезка не существует. Открыв
новый математический объект, пифагорейцы пришли
в полное замешательство. В основе всеобщей
гармонии мира, считали они, должны лежать целые
числа и их отношения. Никаких других чисел они не
знали.
И вдруг эта гармония рушится – существуют
величины, которые отношением целых чисел в
принципе не являются! Это и есть что-то « уму
непостижимое, несоизмеримое, немыслимое» для
пифагорейцев, но не для нас с вами.
4. Выступление «По следам открытия пифагорейцев
Как доказать, что число
иррационально? Предположим, существует
рациональное число ![]() , такое, что
, такое, что ![]() . Дробь
. Дробь ![]() будем считать несократимой (ведь
сократимую дробь всегда можно привести к
несократимому виду). Возведя обе части равенства
в квадрат, получим
будем считать несократимой (ведь
сократимую дробь всегда можно привести к
несократимому виду). Возведя обе части равенства
в квадрат, получим ![]() Отсюда заключаем, что m – число
чётное, т.е. m = 2k. Поэтому и, следовательно,
Отсюда заключаем, что m – число
чётное, т.е. m = 2k. Поэтому и, следовательно, ![]() , или
, или ![]() . Но тогда получается, что
и n также число чётное, а этого быть не может,
поскольку дробь
. Но тогда получается, что
и n также число чётное, а этого быть не может,
поскольку дробь ![]() несократима.
Возникает противоречие. Остаётся сделать вывод,
что наше предположение неверно и рационального
числа
несократима.
Возникает противоречие. Остаётся сделать вывод,
что наше предположение неверно и рационального
числа ![]() , равного
, равного ![]() не существует.
не существует.
История развития теории иррациональности знает много ученых – исследователей. Назовем некоторые из них: это Декарт – французский ученый, английский физик Ньютон, открывший основные законы природы, Лейбниц, Колмогоров, Понтрягин.
5. Выступление
Человеку часто приходиться сталкиваться с
иррациональными числами. Решая задачи на
вычисления длины окружности, площади круга,
приходиться пользоваться формулами![]() , в которых содержится
число
, в которых содержится
число ![]() = 3,14…
= 3,14…
Классическая задача на геометрическую вероятность:
1) Пусть дан квадрат, в который вписана окружность. В квадрат бросают точку; вероятность того, что она попадет в круг, равна отношению площадей круга и квадрата.
![]()
2) В физике при нахождении времяt поднятия тела, брошенного вертикально вверх на высоту h
![]()
3) Диаметр трансмиссионного вала ![]() , где N – мощность станка в
лошадиных силах, n – число оборотов вала в минуту.
, где N – мощность станка в
лошадиных силах, n – число оборотов вала в минуту.
В данном случае речь идет о передачи при
помощи ремня вращения от электромотора к шкиву,
наглухо посаженному на ведомый вал.
4) При вычислении периода колебания
математического маятника ![]()
6. Выступление
В математике есть понятие иррациональное выражение – математическое выражение, содержащее буквы, символы, числа под знаком арифметического корня.
В тождественных преобразованиях радикалов в курсе математики мы используем основных 5 теорем и некоторые специальные приемы уничтожение иррациональности в знаменателе дроби.
Справочные сведения: (раздаточный материал №1 на каждом столе)
Т-1
Если показатель корня – натуральное четное
число, т.е. ![]() , то по
определению
, то по
определению ![]()
Для любого неотрицательного действительного числа а и произвольного натурального числа К существует единственное действительное число в такое, что в2k = a.
Т-2
Если показатель корня – натуральное
нечетное число, т.е. ![]() , то определению
, то определению ![]()
Для любого действительного числа а и произвольного натурального к существует единственное действительное число в такое, что в2k+1 = a.
Неотрицательное значение корня из неотрицательного числа называют арифметическим значением корня. Или просто арифметическим корнем.
Справедливы следующие свойства:
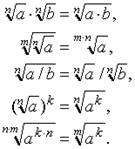
![]() формула
сложного радикала.
формула
сложного радикала.
Учащимся было предложено найти решение для задания1 и представить на семинаре его решение:
Задание 1. При каком целом положительном х значение выражения
![]() ближе
всего к числу 0,7?
ближе
всего к числу 0,7?
Подробное решение у каждого учащегося на парте.На доске заранее записан план решения: Данное выражение определено при выполнении следующих условий:
1. x > 0
2. ![]()
3. ![]()
4. ![]()
Из решения неравенства 1-3 получаем x > 7.
Выполнив преобразования выражения 4 получаем: ![]()
при х = 7 ![]()
при ![]()
следовательно, значения х удовлетворяют условию x > 7.
Преобразуем данное выражение с учетом условия x > 7:
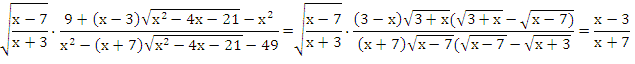
Решая уравнение ![]() получаем
получаем ![]()
Рассмотрим функцию ![]() , т.к.
, т.к. ![]()
Тогда ![]()
![]()
сравним два числа ![]() .
.
Так как ![]()
Ответ 26.
Вступительное слово преподавателя:
Умение преобразовывать радикалы полезно и
необходимо при решении иррациональных
уравнений. Вопросы разрешимости уравнений в
радикалах были окончательно решены только в
первой половине 19 века в работах знаменитых
математиков – итальянца Паоло Руффини,
француза Галуа и норвежца Абеля.
Переходим к решению различных задач
иррациональных уравнений. Решение
иррациональных уравнений требует от вас хороших
теоретических знаний, внимания, трудолюбия,
сообразительности.
Справочные сведения (раздаточный материал №2 для учащихся)
Определение 1
Простейшими иррациональными уравнениями от одной переменной будем называть уравнения вида:
1. ![]()
2. ![]()
3. ![]()
Все корни четной степени, входящие в иррациональное уравнение, являются арифметическими. Все корни нечетной степени определены при любом действительном значении подкоренного выражения, при этом корень имеет тот же знак, что и подкоренное выражение.
Алгоритм решения каждого из типов простейших уравнений:
1. ![]()
2. Функция ![]()
Поэтому ![]()
Задание 2. Решить уравнение ![]()
План решения:
Уравнение решаем методом замены переменной.
получаем уравнение ![]() , решая, получаем
, решая, получаем ![]()

1. Найти нули функции: ![]()
2. Найти сумму корней уравнения: ![]()
План решения
Данное уравнение равносильно совокупности
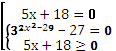
Решая, получаем: х = – 3,6
х = 4; х — 4х
![]()
учитывая данные условия, имеем – 3,6 + 4 = 0,4. Ответ: 0,4
3. Решить уравнение ![]()
План решения:
Т.к. функция ![]() возрастающая,
возрастающая, ![]() убывающая.
убывающая.
Уравнение имеет не более одного корня х = – 2. Подставив в данное уравнение х = – 2, получим верное числовое равенство.
Выступление 7. Решение иррациональных неравенств
Справочные сведения. Раздаточный
материал 3.Решение простейших иррациональных
неравенств.
Решение неравенств, содержащихся под знаком
радикала, основано на теоремах:
Т-1:
![]()
T-2:
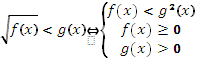
T-3:
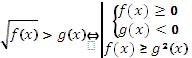
Задание: решить неравенство и указать
число целых отрицательных решений неравенства ![]()
План решения:
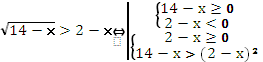
Решая совокупность двух систем получаем ![]()
![]()
Неравенству удовлетворяет одно отрицательное целое значение х = – 1.
Итоги урока:
«Числа управляют миром», – говорили пифагорейцы. Мы не можем согласиться с данным утверждением,мы знаем, что не число есть основа вещей, хотя, несомненно, число играет исключительную роль в науке и технике, в деле подчинения ее сил человеку.Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе.
Используемая литература к семинару:
- Иррациональные числа на сайте: ru.wikipedia.org›wiki/
- Современный толковый словарь изд. «Большая Советская Энциклопедия».
- А. Киселев. Элементы алгебры и начала анализа. Пятое издание. Издательство Москва. 1928.
- Учебник Алгебра и начала математического анализа 10-11. Ш. Алимов.
- В.Б. Некрасов. Школьная математика. Самое необходимое. «Авалон». С-Петербург.2006.