Цель работы: Разработать модель решения геометрических задач практического содержания из вариантов ГИА 9 класса и создать демонстрационную презентацию данного метода.
Литература:Открытый банк заданий по математике ГИА 2012 www.mathgia.ru
Этапы решения задачи:
- Постановка задачи
Формулируется условие задачи, выделяются исходные данные и результаты. - Создание математической модели
Строится математическая модель решения задачи, например, выполняется геометрический чертеж, в котором реальные объекты заменены на геометрические фигуры. - Вычислительный этап
Производится сопоставление теоретического материала с созданной математической моделью. Выписываются расчетные формулы, выделяются существенные свойства геометрических объектов.
Производятся расчеты. - Анализ полученных результатов
Производится сопоставление результата решения задачи реальной действительности.
Задача 1. В 24 м одна от другой растут две сосны. Высота одной 23 м, а другой – 16 м. Найдите расстояние (в метрах) между их верхушками.
| Этапы решения задачи | Содержание |
| Постановка задачи | Условие задачи: В 24 м одна от другой растут две сосны. Высота одной 23 м, а другой – 16 м. Найдите расстояние (в метрах) между их верхушками. Исходные данные: Высоты деревьев – 23 м и 16 м, расстояние между их основаниями – 24 м. Результат: Расстояние между верхушками сосен. |
| Создание математической модели | 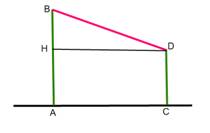 AB=23 м, CD=16 м, АС=24 м Найти BD |
| Вычислительный этап | Теоретический минимум: В прямоугольнике противоположные стороны равны. Длина отрезка равна сумме длин частей, из которых состоит этот отрезок. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Решение: Проведем DH перпендикулярно АВ, ACDH – прямоугольник, DC=AH, AC=DH. ВН=АВ-АН. Таким образом, DH=24 м, BH=23–16=7 м. По теореме Пифагора: |
| Анализ полученных результатов | Можно сопоставить полученный результат 25 м, например, с расстоянием между соснами 24 м. |
Задача 2. Человек ростом 1,7 м стоит на расстоянии 8 шагов от столба, на котором висит фонарь. Тень человека равна четырем шагам. На какой высоте (в метрах) расположен фонарь?
| Этапы решения задачи | Содержание |
| Постановка задачи | Условие задачи: Человек ростом 1,7 м стоит на расстоянии 8 шагов от столба, на котором висит фонарь. Тень человека равна четырем шагам. На какой высоте (в метрах) расположен фонарь? Исходные данные: Рост человека – 1,7 м, тень человека – 4 шага, расстояние от человека до столба – 8 шагов. Результат: Высота столба (в метрах). |
| Создание математической модели |
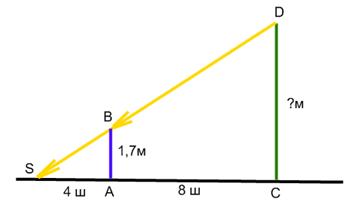 AB=1,7 м, SA=4 шага, AC=8 шагов Найти СD |
| Вычислительный этап | Теоретический минимум: Первый признак подобия треугольников (по двум углам). Длина отрезка равна сумме длин частей, из которых состоит этот отрезок. Решение: CS=AC+AS=4+8=12 шагов. DS – луч света от фонаря. ΔABS~ΔCDS (по двум углам). Тогда |
| Анализ полученных результатов | Можно сопоставить полученный результат 5,1 м, например, с ростом человека 1,7 м. |
Прототипы задач с практическим содержанием из открытого банка заданий ГИА 2012
- Мальчик прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел 600 м. На каком расстоянии (в метрах) от дома оказался мальчик?
- Девочка прошла от дома по направлению на запад 500 м. Затем повернула на север и прошла 300 м. После этого она повернула на восток и прошла еще 100 м. На каком расстоянии (в метрах) от дома оказалась девочка?
- Мальчик и девочка, расставшись на перекрестке, пошли по взаимно перпендикулярным дорогам, мальчик со скоростью 4 км/ч, девочка – 3 км/ч. Какое расстояние (в километров) будет между ними через 30 минут?
- Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 15 км/ч и 20 км/ч. Какое расстояние (в километрах) будет между ними через 2 часа?
- В 60 м одна от другой растут две сосны. Высота одной 31 м, а другой – 6 м. Найдите расстояние (в метрах) между их верхушками.
- Колесо имеет 18 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы.
- Сколько спиц в колесе, если угол между соседними спицами равен 18°?
- Какой угол (в градусах) образуют минутная и часовая стрелки часов в 5 ч?
- Какой угол (в градусах) описывает минутная стрелка за 10 мин?
- Какой угол (в градусах) описывает часовая стрелка за 20 мин?
- На какой угол (в градусах) поворачивается минутная стрелка пока часовая проходит 2°?
- Человек ростом 1,7 м стоит на расстоянии 8 шагов от столба, на котором висит фонарь. Тень человека равна четырем шагам. На какой высоте (в метрах) расположен фонарь?
- Человек ростом 1,8 м стоит на расстоянии 12 м от столба, на котором висит фонарь на высоте 5,4 м. Найдите длину тени человека в метрах.
- Площадь прямоугольного земельного участка равна 9 га, ширина участка равна 150 м. Найдите длину этого участка в метрах.
- Найдите периметр прямоугольного участка земли, площадь которого равна 800 м2 и одна сторона в 2 раза больше другой. Ответ дайте в метрах.
- Сколько досок длиной 2 м, шириной 20 см и толщиной 10 мм выйдет из четырехугольной балки длиной 100 дм, имеющей в сечении прямоугольник размером 50 см × 80 см?
- Сколько коробок в форме прямоугольного параллелепипеда размерами 30×40×100 (см) можно поместить в кузов машины размерами 2,4×8×2,8 (м)?
- Две трубы, диаметры которых равны 45 см и 60 см, требуется заменить одной, не изменяя пропускную способность. Каким должен быть диаметр новой трубы? Ответ дайте в сантиметрах.
- Сколько потребуется кафельных плиток квадратной формы со стороной 30 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 2,7 м и 4,8 м?
- Пол комнаты, имеющей форму прямоугольника со сторонами 7 м и 8 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 20 см. Сколько потребуется таких дощечек?
- Найдите периметр прямоугольного участка земли, площадь которого равна 19600 м2 и одна сторона в 4 раза больше другой. Ответ дайте в метрах.
- Площадь прямоугольного земельного участка равна 14 га, ширина участка равна 100 м. Найдите длину этого участка в метрах.