Формирование логического мышления – важная составная часть педагогического процесса. Помочь учащимся в полной мере проявить свои способности, развить инициативу, самостоятельность, творческий потенциал – одна из основных задач современной школы. Успешная реализация этой задачи во многом зависит от сформированности у учащихся познавательных интересов.
Математика даёт реальные предпосылки для развития логического мышления, задача учителя – полнее использовать эти возможности при обучении детей математике.
Традиционно проблема развития познавательного интереса ребенка решается средствами занимательности в обучении математике. Однако следует больше использовать так называемую “внутреннюю” занимательность самой математики, тесно связанную с изучаемым учебным материалом, и врожденную любознательность маленьких детей. Внутренняя занимательность – это появление необычных, нестандартных ситуаций с уже знакомыми детям понятиями, возникновение новых “почему” там, где, казалось бы, все ясно и понятно (но только на первый взгляд). Это, наконец, проникновение в методику элементов игровой деятельности, которая, естественно, присуща ребенку. Чему нужно научить ребенка при обучении математике? Размышлять, объяснять получаемые результаты, сравнивать, высказывать догадки, проверять, правильные ли они; наблюдать, обобщать и делать выводы.
В начальной школе особенно важно дать правильное представление о вводимых математических понятиях, это обусловливается тем, что первоначально формируемый образ является наиболее устойчивым, а, как известно, переучивать всегда сложнее. Чтобы с самого начала дать правильное представление, сформировать верное математическое понятие, необходима система специально подобранных заданий, которые раскрывали бы сущность понятия. При составлении таких заданий следует ориентироваться на те умения учащихся, которые характеризуют сформированность понятия. Среди них такие умения: давать определение понятия, самостоятельно формулировать существенные признаки понятия, выводить следствие из факта принадлежности к данному понятию, приводить свои примеры объектов, принадлежащих понятию. Рассмотрим это на конкретных примерах. Для того чтобы говорить о полноценном усвоении понятия “прямоугольник” в начальных классах, нужно предложить учащимся задания, в которых необходимо:
— назвать существенные признаки прямоугольника: четыре угла, четыре стороны, четыре вершины, все углы прямые, противоположные стороны равны;
— выбрать из предложенных геометрических фигур прямоугольники;
— самостоятельно начертить прямоугольник на клетчатой бумаге;
— привести примеры геометрических фигур, которые не являются прямоугольниками, находить прямоугольник в окружающей обстановке.
Для составления заданий, направленных на усвоение смысла умножения, необходимо прежде всего выделить существенные и несущественные признаки этого понятия. К первым относятся: произведение — это сумма (при а > 1); слагаемые в этой сумме равны. Несущественные признаки: количество слагаемых, какие это слагаемые (одно-, двух- или трехзначные числа). Именно поэтому для формирования понятия “умножение” можно предложить ученикам следующие задания:
1. Вставьте пропущенные числа так, чтобы получилось верное равенство:
48 + 48 + 48 + 48 + 48 = … • 5
51 + 51 + 51 + 51 = 51 • …
14 + … + 14 + 14 + 14 + 14 = 14 • б
22 + 22 + … = … • 3
8+8+8+…=8-…
2. Вставьте пропущенные знаки так, чтобы получилось верное равенство:
18 * 18 * 18 * 18 * 18 * 18 = 18 • 6 45 + 45 = 45 * 2
8*8*8*8*8*8*8*8=8*8
(35 - 24) * 2 = (35 - 24) + (35 - 24)
3. Замените сложение умножением: 12 + 12 + 12 + 12 + 12
0 +0 + 0 + 0. + 0 + 0 + 0
33 + 33 + 33
4 + 4 + 4 + 4
1+1+1+1+1+1
(3 + 21) + (3 + 21)
…+…+…+...
4. Замените умножение сложением:
4-8
99-2
(17 + 5)-3
О-5
1-10
0-7
(14-11)-2
…-7
5. Найдите и исправьте ошибку: 81 + 81 = 81 • 2
44 + 44 + 44 + 44 = 44 + 4
17+ 17- 17+ 17- 17 = 17- 5
21 • 3 = 21 + 22 + 23
6. Не вычисляя, докажите, что равенство верно: 9-5=9+9+9+9+9 27 + 27 + 27 = 27 • 3
7. Дети построились так, что их удобно сосчитать следующим образом:
8•3. Нарисуйте треугольники так, как построились дети. А потом некоторые дети разбились на группы, что их легко было сосчитать так:
8 + 3 + 2. Нарисуйте кружочки так, как дети разбились на группы.
8. Нарисуйте елочки, чтобы их можно было сосчитать так: 2 • 6. А если их можно будет сосчитать так: 2 + 6, то как следует сделать рисунок?
9. К каждому рисунку запишите соответствующий пример:

10.Сравните и поставьте знак >, < или =, чтобы записи были верными: 38 + 38 + 38 ... 38 *3
16 • 6 ... 16 + 16 + 16
44 + 44 + 44 + 44 ... 44 • 5
16 + 16 + 16 ... 20-3
11. Вставьте пропущенное число, чтобы неравенство было верным:
10 + 10 + 10 + … < 10 • 4
43 + 43 + 43 > 43 • …
5+5+5+5+5<…•5
Данные задания можно предлагать учащимся в процессе устного счета. Наиболее трудные из них первоначально лучше предложить более сильным учащимся в качестве индивидуального задания, а потом разобрать их со всем классом. Такие задания целесообразно использовать не только при введении понятия “умножение”, но и в течение всего учебного года. Они позволяют осуществлять систематическое повторение, но каждый раз на новом уровне.
Систематически работая над формированием математических понятий, используя продуманные системы заданий, учитель создает основу математического мышления у младших школьников, способствует развитию устойчивого интереса к математике.
Познавая предметы и явления окружающей действительности, мы можем мысленно расчленять предмет или явление на составные части и мысленно же соединять части в одно целое. Операция мышления, направленная на расчленение целого на составляющие его части, называется анализом. Операция мышления, направленная на установление связи между предметами или явлениями, называется синтезом. Эти операции мышления взаимно связаны.
Уже на первых шагах обучения при изучении чисел первого десятка учащиеся пользуются наглядно-действенным анализом (разложением) предметных множеств на составляющие их элементы и наглядно-действенным синтезом (соединением), группируя элементы во множества.
Наглядный анализ и синтез сменяется затем анализом и синтезом по представлению: ребёнок может выполнить разложение чисел или их соединение, оперируя со зрительными образами, которые сохраняются в его памяти и могут быть воспроизведены в его сознании.
Более высокой ступенью является умственный анализ и синтез, выполняемый мысленно при помощи внутренней речи.
При обучении любому разделу математики приходится опираться на анализ и синтез. Приведу примеры некоторых заданий:
1.Задания на рассмотрение данного объекта с точки зрения различных понятий.
А) Прочитайте выражения разными способами: 18+16 и 34-16. Сравните данные выражения. Что заметили?
Б) Малыш и Карлсон играли в игру: поочерёдно записывали цифры в ряды. Карлсон записывал любые цифры, а Малыш – по одному и тому же принципу. Подумай, по какому принципу записывал Малыш цифры, и допиши те, которые он не дописал.
Карлсон |
9 |
4 |
7 |
11 |
19 |
3 |
8 |
6 |
Малыш |
7 |
2 |
5 |
В данной таблице надо уловить особенность изменения чисел, тогда ты поймёшь, какие числа надо дописать.
В) Из различных бус я сделал бусы,
но бусы были порваны.
Кто сможет их помочь собрать,
Тому бы я поставил 5.
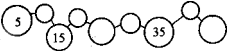
2. Задания на узнавание объектов по данным признакам.
А) Какой предмет обладает одновременно следующими признаками: имеет 3 стороны и 3 угла.
Б) узнай и запиши числа:
- Число больше 10, чётное, получается при выполнении действия между числами 6 и 2 (6?2 = 12)
- Число нечётное, больше 5, при умножении его на 4 получается 36 (9)
В) К учителю подошли 6 ребят. Каждый сдал по 2 тетрадки. Какое арифметическое действие должен выполнить учитель, чтобы определить, сколько тетрадок сдали дети?
3. Постановка различных заданий к данному математическому объекту.
А) Используя три числа 8, 3, 24, придумай различные задания.
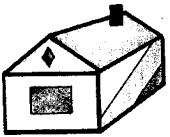
Б) . Вот волшебный дом, много фигур в нем.
Какие фигуры ты заметил, расскажи.
И сколько четырехугольников, запиши. (6.) -
Сколько отметок нужно сделать, чтобы разделить трубу на 4 части? (3.)
В процессе начального обучения математике находит своё применение приём сравнения, т.е. выделение сходных и различных признаков у рассматриваемых чисел, арифметических примеров, арифметических задач.
Приведу примеры заданий на сравнение:
А) Задания на обнаружение сходных признаков
1. Чем похожи числа 7 и 71? (В записи чисел используется цифра 7; эти числа нечетные.)
2. Что общего в числах 12, 26, 28, 24, 82, 62? (Числа двузначные; делятся на 2; четные; в записи каждого есть цифра 2.)
3. Назови общие признаки чисел, получаемых в результате действий 42 : 6; 48 : 6. (7 и 8 - однозначные числа; меньше 10.)
Б) Задания на обнаружение отличных признаков:
1. Найди “лишний” рисунок.
2. Чем отличаются равенства (9+2)*2 =22 9*2 +2*2 =22
3. Найди “лишний” ряд. Чем он отличается от других?
1,2,4,8,16
2,6,18,54,162
5,10,20,40,80
7,14,28,56,112
В) Задания на полное сравнение
1. Найди сходства и различия
2. Вставь недостающую фигуру
3. Найди одинаковые фигуры, домики…
Анализ и синтез, как взаимосвязанные мыслительные операции находят своё применение при решении текстовых задач.
Ученик под руководством учителя, прежде всего, анализирует содержание задачи, расчленяя его на числовые данные, условия и вопрос.
При решении составных арифметических задач требуется применить более сложный и более тонкий анализ и синтез. Анализ содержания составной задачи, так же как и простой, сводится к расчленению его на числовые данные, условия и вопрос. Однако сами данные, условие и искомое должны подвергнутся дополнительно анализу, расчленению на составляющие их элементы.
После решения задач учащиеся сравнивают, каким действием решается та или другая задача: одна сложением, другая умножением, а затем сопоставляют способы решения с различиями в условиях задач. Такое сопоставление помогает учащимся лучше осознать смысл выражений “больше на несколько единиц” и “больше в несколько раз” и прочнее установить связь между условием каждой задачи и способом её решения.
Сравнение основано на анализе и синтезе: необходимо расчленить каждую задачу на составляющие её элементы, а затем мысленно соединить сходные элементы, выделив при этом существенные различия.
При объяснении учащимся новой для них по способам решения задачи с многозначными числами часто используется приём аналогии: учитель предлагает решить аналогичную задачу с небольшими числами, вычисления над которыми можно выполнить устно.
Наибольший эффект развития логического мышления может быть достигнут в результате применения различных форм работы над задачей:
- Работа над решённой задачей. Многие учащиеся только после повторного анализа осознают план решения задачи. Это путь к выработке твёрдых знаний по математике. Конечно, повторение анализа требует времени, но оно окупается.
- Решение задач различными способами. Это умение свидетельствует о достаточно высоком математическом развитии.
- Правильно организованный способ анализа задачи – с вопроса или от данных к вопросу.
- Представление ситуации, описанной в задаче. Учитель обращает внимание детей на детали, которые нужно обязательно представить, а которые можно опустить. Мысленное участие в этой ситуации. Разбиение текста задачи на смысловые части. Моделирование ситуации с помощью чертежа, рисунка.
- Самостоятельное составление задач учащимися.
- Решение задач с недостающими или лишними данными.
- Изменение вопроса задачи.
- Составление различных выражений по данным дадачам и объяснение, что обозначает то или иное выражение.
- объяснение готового решения задачи.
- Использование приёмов сравнения задач и их решений.
- Запись двух решений на доске – одного верного, а другого неверного.
- Изменение условия задачи так, чтобы задача решалась другим действием.
- Закончить решение задачи.
- Какой вопрос или действие лишнее в решении задачи.
- Восстановить пропущенный вопрос или действие в задаче.
- Составление аналогичной задачи с изменёнными данными.
- Решение обратных задач.
Задания, направленные на развитие наблюдательности, которые тесно связаны с такими приёмами развития логического мышления, как анализ, сравнение, синтез и обобщение:
- Чем отличаются и чем похожи данные выражения?
- Найди результат, пользуясь решённым примером.
- Продолжи данный ряд чисел.
Задания для самостоятельного выявления закономерностей, зависимостей и формулировки обобщения:
1.Сравни примеры, найди общее и сформулируй данное правило.
2. Сравни условия задач, их решения. Сделай вывод.
3. Сравни примеры в каждом столбике, найди правило по которому они составлены и продолжи столбики примеров.
Уметь классифицировать объекты – неотъемлемое качество логически мыслящей личности.
Формирование этого умения необходимо начинать с самого начала обучения.
Применение приёма классификации на уроках математики позволяет расширить имеющиеся в практике приёмы работы, способствуют формированию положительных мотивов в учебной деятельности, так как подобная работа содержит элементы игры и элементы поисковой деятельности, что повышает активность учащихся и обеспечивает самостоятельное выполнение работы.
На уроках математики использую задания на классификацию геометрических объектов, классификация примеров, задач.
Например:
1.Убери лишний предмет, нарисуй фигуру такого же цвета (формы, размера), дай названия группе предметов, сравни похожие рисунки, найди отличия.
2. Задания, в которых указывается основание классификации: Разбей числа на группы – однозначные и двузначные, чётные и нечётные. Разбей примеры на группы, чтобы в каждой были похожи записи или одинаковые результаты.
3. Задания, в которых надо выделить объекты из данной группы по определённому основанию, а затем указать основания для оставшейся группы объектов- выпиши все числа, записанные двумя различными цифрами 22, 56, 80, 66, 74, 88, 31, 94, 44. Посмотрите на оставшиеся цифры и назовите признак, являющийся общим для них, т. е. указать основание.
Но особенно эффективными для развития логического мышления являются задания, в которых основание для классификации выбирают сами дети.
Так же использую графические схемы. Например, сделай графическую схему к задаче, доведи до конца частично заполненные схемы, составь выражение или задачу по данной графической схеме, составь графическую схему по условию.
Использую на уроках специальные задачи и задания, направленные на развитие познавательных возможностей и способностей детей. Нестандартные задачи требуют повышенного внимания к анализу условия и построения цепочки взаимосвязных логических рассуждений.
Например: Бублик разрезали на 4 части. Сколько сделали разрезов?
Или: В коробке лежит 5 карандашей: 2 синих и 3 красных. Сколько карандашей надо взять из коробки, не заглядывая в неё, чтобы среди них был хотя бы 1 красный карандаш?
Нестандартные задачи ввожу с 1 класса, так как они расширяют математический кругозор, способствуют математическому развитию и повышают качество математической подготовки. На уроках математики стремлюсь отвести время на работу с заданиями, развивающими логическое и абстрактное мышление. Для этого предлагаю примеры с окошками и пропущенными знаками. Данные задания имеются в учебнике и в тетрадях на печатной основе, главное, отобрать и применить на нужном этапе на уроке.
Решение нестандартных задач позволяет приучить детей к правильности и чёткости рассуждений, к критическому осмыслению полученных результатов, развивает у них гибкость, вариативность мышления.
Эффективность обучения младших школьников решению нестандартных задач зависит от нескольких условий:
1. Задачи следует вводить в процесс обучения в определённой системе с постепенным нарастанием сложности, так как непосильная задача мало повлияет на развитие учащихся.
2. Необходимо предоставлять ученикам максимальную самостоятельность в поиске решения задач, давать возможность пройти до конца по неверному пути, убедиться в ошибке, вернуться к началу и искать другой путь решения.
3. Нужно помочь учащимся осознать некоторые способы, общие подходы к решению нестандартных арифметических задач.
Обучение младших школьников решению нестандартных задач можно разделить на 2 этапа:
1. Проводится специальная работа по выводу и осмыслению общих подходов к решению таких задач. При этом важно, чтобы ученики уже усвоили процесс решения любой задачи, познакомились с приёмами работы на на каждом этапе решения задачи (виды наглядной интерпретации, поиска решения, проверки решения и т. д.).
2. Применяют ранее сформулированные общие приёмы в ходе самостоятельного поиска решения конкретных задач.
Рекомендации при решении нестандартных задач:
1.Для того чтобы решить задачу, бывает полезно построить к ней рисунок или чертёж. Ответ в некоторых случаях может быть получен только из чертежа без выполнения арифметических действий.
Например: Бревно длиной 12 м распилили на 6 равных частей. Сколько распилов сделали?
2. При поиске решения незнакомой задачи полезно сделать чертёж (рисунок), так как работа с ним может являться способом решения задачи.
Например: Лестница состоит из 9 ступенек. На какую ступеньку надо встать, чтобы оказаться на середине лестницы?
3. Для того чтобы решить задачу, бывает нужно ввести вспомогательный элемент (часть).
Например: Разложи 45 шариков в 4 коробки так, что если число шариков в 3 коробке увеличить в 2 раза, а в 4 коробке уменьшить в 2 раза, а в первой и второй оставить без изменения, то в каждой коробке будет одинаковое число шариков.
В процессе поиска решения данной задачи использовали несколько приёмов: строили и достраивали чертёж, вводили вспомогательный элемент (часть – примем число шариков в 3 коробке за 1 часть, тогда число шариков в 4 коробке составит 4 части, в 1 – 2 части, во 2 – 2 части). Его удобно ввести, когда на чертеже получены отрезки одинаковой длины.
4. В поиске ответа на вопрос можно использовать способ подбора.
Например: Сумма четырёх различных чисел равна 13. Наименьшее из этих чисел на 5 меньше наибольшего. Найди эти числа.
5. При решении нестандартных задач полезно переформулировать задачу, т. е. сказать её другими словами, чтобы она стала знакомой и понятной.
Например: Если конфеты раскладывать по 2, 3, 4, то всегда остаётся одна лишняя. А если их раскладывать по 5, то лишних конфет нет. Сколько конфет, если их меньше 50? ( Т. е. это число делится на 5 без остатка, а на 2, 3, 4 есть остаток 1 и оно меньше 50).
6. Условие или вопрос задачи можно разделить на части и решить задачу по частям.
Например: 18 ручек стоят на 30 руб больше, чем 30 карандашей. Те же 18 ручек стоят на 10 рублей больше, чем 40 таких же карандашей. Сколько стоит 1 карандаш и 1 ручка?
7. Решать задачу можно, начиная “с конца”.
Например: Девочка начертила 4 отрезка. Каждый следующий отрезок она делала на 2 см длиннее предыдущего. Найди длину первого отрезка, если длина 4 отрезка равна 12 см.
Сформулированные рекомендации по решению нестандартных задач объединяются в следующей памятке:
Если тебе трудно решить задачу, то попробуй:
- Сделать к задаче рисунок или чертёж; подумай, может быть, нужно сделать на них дополнительные построения или изменить чертёж в процессе решения задачи;
- Ввести вспомогательный элемент (часть).
- Использовать для решения задачи способ подбора.
- Переформулировать задачу другими словами, чтобы она стала более понятной и знакомой.
- Разделить условие или вопрос на части и решить её по частям.
- Начать решение задачи “с конца”.
Важно объяснить детям, что данные указания носят рекомендательный характер. Необязательно применять их в той последовательности, как они записаны в памятке, необязательно выполнять все рекомендации при решении одной задачи, можно комбинировать их в разных сочетаниях. В этом суть творческого процесса решения нестандартных задач.
Изложенная мной система работы по развитию логического мышления направлена на формировании умственных действий учащихся. Логические задачи и упражнения позволяют расширять математический кругозор и позволяют более уверенно ориентироваться в простейших закономерностях окружающей их действительности и активнее использовать математические знания в повседневной жизни.
Литература
1. Бескоровайная Л.С., Перекатьева О. В. Методика современного открытого урока, Феникс, Ростов-на- Дону,2003.
2. Баранов С.П, Чиркова Н.И Развитие логики мышления младших школьников., Нач. шк., 2006, №12.
3. Бадмаев Б. Ц. Психология в работе учителя, ВЛАДОС, М, 2000.
4. Волкова С.И. Задания развивающего характера в новом едином учебнике “Математика”, Нач. шк., 1997, №9.
5. Гамезо М. В., Домашенко И. А. Атлас по психологии, Российское Педагогическое Агентство, М, !998.
6. Коломинский Я. Л. Человек : психология М “Просвещение” 1980.
7. Копытов Н. А. Задачи на развитие логики. М. “АСТ – ПРЕСС” 1998.
8. Левитас Г. Г. Нестандартные задачи в курсе математики в нач.шк., Нач. шк. 2001. №5