Как показывает проведенный в гимназии опрос среди учащихся и родителей понятие «критическое мышление» ассоциируется в их восприятии с поиском недостатков, недочетов. И зачастую наша учительская работа бывает слишком наполнена стремлением исправить ошибки, направить детей и взрослых на путь истинный, который лично нам абсолютно понятен как единственно верный.
В то же время уже много лет говорится об отсутствии монополии на истину у учителя, о неоднозначности подходов к её поиску.
Нам, учителям математики, в какой-то мере в этих обстоятельствах особо сложно приходится. Ведь у историков, лингвистов, социологов, психологов так много субъективного в подходах к познанию, а у нас дважды два – четыре, утверждение или истинно, или ложно, и только, пожалуй, теория вероятностей заставляет нас задуматься о месте неопределенности в математике и жизни. И, тем не менее, мы, наверняка, столь же субъективны в своих подходах, как те же «гуманитарии», когда речь заходит о контакте нашей личности с личностью ученика. Высокий уровень осмысленности процесса обучения со стороны ребенка может стать для нас реальной проблемой.
«Дети стали не те», «родители совершенно невозможны». Такие фразы можно слышать по нескольку раз в день. Но никакого иного пути нет, как сделать первыми шаг навстречу нашим ученикам и их сложным родителям и попытаться взвесить свои возможности на пути конструктивного сотрудничества.
Лично мне не нравится слово «технология» применительно к образованию. Мы ведь знаем, что даже испеченные по одной и той же технологии торты имеют совершенно разный вкус.
Признание за учеником права на собственную оценку ситуации дает нам возможность вступления с ним в диалог на основе принципов сотрудничества, совместного планирования и осмысления совершаемых действий. Нам показалось интересным сравнить подходы учащихся разных классов и разных школ, их готовность осмыслить, что не дает возможности быть успешными на математическом поприще, как применить имеющийся опыт и знания для решения непростых математических задач.
Сами по себе фазы технологии развития критического мышления просты, но увлекательны.
Вызов – Осмысление – Рефлексия. В работе с учениками мне всегда хочется заглянуть за горизонт – за горизонт нынешних возможностей, за порог имеющихся способностей. Чем, как ни словом «вызов» можно характеризовать соответствующее действие? «Слабо?».
И подростки поддаются на эту провокацию. В этой статье хотелось бы рассказать об опыте проведения занятий с аудиторией учащихся 9-10 классов, для которой брошенной перчаткой стали два задания С3 и С5 из вариантов диагностических работ при подготовке к ЕГЭ – задачи с модулем и с параметром, которые обычно остаются за пределами наших уроков, где-то для себя мы определяем , особенно последнее, словами «не тронь лиха».
В состав участников трех занятий по данной тематике вошли учащиеся, как профильных, так и общеобразовательных классов, в базе знаний которых предварительно были восстановлены определения понятий модуль и параметр. Одной из задач, решаемых в ходе проведенных занятий, было осознание факта, что встречающиеся на ЕГЭ задачи из группы С в 11 классах зачастую действительно не требуют для успешного решения знаний, выходящих за рамки школьной программы основной школы. Мне очень понравилась краткая подборка афоризмов, которую создали ребята для комментариев своей деятельности. Одно высказывание, вынесенное в заголовок статьи, встречалось неоднократно: «Благоприятная возможность скрывается среди трудностей и проблем» (А. Эйнштейн).
Помимо главной цели занятий – развития критического мышления учащихся существуют и задачи по развитию важных способностей и умений: умение работать с увеличивающимся и постоянно обновляющимся информационным потоком; умение выражать свои мысли ясно, уверенно и корректно по отношению к окружающим; умение вырабатывать собственное мнение на основе осмысления различного опыта, идей и представлений; умение решать проблемы; способность самостоятельно заниматься своим обучением (академическая мобильность); умение сотрудничать и работать в группе; способность выстраивать конструктивные взаимоотношения с другими людьми.
После проведения входного мини-теста учащимся была предложена мозаичная модель, отдельные элементы которой необходимо было собрать, чтобы оценить свой потенциал и обратить внимание на недостающие элементы для успешного решения задания.
Среди набора представленных задач присутствуют два подкласса заданий, используя идеи которых, можно решить задачи С3 и С5 ЕГЭ, если в нужной последовательности без ошибок собрать соответствующие части мозаики. Поскольку часть утверждений или вопросов для участников занятий могла быть новой или непонятной, им было предложено начать работу с классификации их по группам:
I – потребуется для С3 II – потребуется для С5
Внутри же каждой группы для реализации поставленной цели занятия было предложено разделить задания на подгруппы по признакам:
Знаю Хочу узнать Узнал
Участники занятий разделились на группы по 5-7 человек, более близкое знакомство на первом занятии предполагало возможность разделения ролей внутри группы при работе на последующих занятиях.
Используя совместный потенциал собственных знаний и знаний группы, участники могли произвести обмен полезной информацией. К концу занятий результативность работы команды определялась по индивидуальному продвижению каждого участника и по полноте предлагаемой блок-схемы для решения заданий ЕГЭ. В качестве домашнего задания группам участников было предложено представить презентации уроков, которые они бы могли провести для одноклассников, чтобы научить их справляться с похожими задачами.
С3. Решите неравенство ![]() .
.
С5. Найдите все значения параметра а, при
каждом из которых неравенство ![]() имеет единственное целое
решение.
имеет единственное целое
решение.
Мозаика
1. Изобразите на плоскости Оху множество точек,
координаты которых удовлетворяют: уравнению ![]() неравенству
неравенству ![]()
2. Решите неравенства ![]()
3. Умеете ли вы в координатах задавать
пересечение полуплоскостей?
4. ![]()
![]() Можете ли Вы аналитически
решить эти неравенства и представить
графическую интерпретацию этих решений на
плоскости Oba?
Можете ли Вы аналитически
решить эти неравенства и представить
графическую интерпретацию этих решений на
плоскости Oba?
5. Знаете ли Вы определение ![]()
6. Умеете ли Вы находить множество значений
квадратного трехчлена?
7. В чем по смыслу отличаются высказывания:
единственное целое решение; единственное
решение, причем целое?
8. Каким свойством обладает график квадратичной
функции относительно вертикальной прямой,
проходящей через вершину параболы?
9. Знаете ли вы формулу для абсциссы вершины
параболы?
10. Чем отличается параметр от неизвестной
величины?
11. Умеете ли вы находить решение системы
квадратичных неравенств?
12. Умеете ли Вы находить решение совокупности
квадратичных неравенств?
13. Когда целесообразно проводить замену
переменных?
14. Что проще: решить линейные или квадратичные
неравенства?
15. Какие значения квадратичная функция принимает
только при одном значении аргумента?
16. Как на координатной плоскости Opt выглядит
множество точек, имеющих одно и то же значение
ординаты t?
17. Что является решением неравенства с одним
неизвестным и одним параметром?
18. Чем отличаются способы решения неравенств
вида ![]() «по
определению модуля» и «по свойству модуля»? В
каких обстоятельствах один из них является
предпочтительным?
«по
определению модуля» и «по свойству модуля»? В
каких обстоятельствах один из них является
предпочтительным?
19. Если вы знаете целое число, которое должно
войти в искомое непрерывное числовое множество,
какие ограничения надо ввести, чтобы других
целых чисел в это множество не попало?
20. Умеете ли Вы находить координаты точки
пересечения двух прямых на плоскости, заданных
аналитически?
21. Какие особенности можно отметить в
аналитическом способе задания прямых,
параллельных друг другу?
22. Понимаете ли Вы слова «равносильность»,
«следствие» применительно к уравнениям и
неравенствам?
23. Умеете ли Вы пользоваться знаками следствия и
равносильности при выполнении математических
преобразований?
Хочется сразу признаться, что задание С3 было только «затравкой» для работы с заданием С5.
В ходе первого занятия проявилось несколько тенденций среди групп учащихся: одни сразу стали мужественно раскрывать модули, что существенно усложняло и затягивало задачу. Другие обратили внимание общность структуры заданий и не торопились принимать какой-то план действий.
В ходе занятия следовало проявлять максимальную гибкость и аутентичность преподавателя каждой учебной ситуации. Проявляя уважение к выбранной учениками позиции, необходимо было обратить их внимание на возможность иного подхода к проблеме.
Для домашнего анализа участникам занятия был
предложен вариант авторского решения задания (
диагностическая работа МИОО 2010 г), который
базируется на замене переменных ![]()
![]() и
последующем исследовании поведения функции
и
последующем исследовании поведения функции ![]() на основе
построения её графика.
на основе
построения её графика.
Радость в предвкушении избавления от последующих забот одних участников ( которые планировали разобраться в представленном решении и его запомнить) сочеталась с недоумением других: зачем давались «подсказки» в мозаике №16, №18, какая замена переменных позволит справиться с заданием С3?
Но наиболее интересным мне показались вопросы учеников, как составляются подобные задачи и существует ли общий подход к их разработке.
На втором занятии группы участников оценивали свою работу. Кроме того, появились два новых способа решения, предложенных в группах: первый из них не предполагал построения вообще никаких графиков и сводил работу к решению возникающих многочисленных квадратичных неравенств в ходе раскрытия скобок модуля. Другой способ привлек использование метода областей на координатной плоскости, одна из осей которой была связана с переменной, а другая – с параметром исходного неравенства.
Ниже рассматривается последний вариант решения, поскольку презентация результатов участника этого направления была наиболее успешной.
Очень хочется, чтобы заинтересованный читатель просмотрел Приложение 1, которое содержит презентацию, созданную Ольховой Анной при моей поддержке, поскольку в ней реализуется попытка максимально возможно отразить эмоциональную реакцию участника занятия на представленное для него задание и последовательность шагов, которая постепенно привела к его успешному выполнению.
Конструирование решения
Реализуем правило 1: внимательно вчитываясь в
условие, отыскиваем ключевые слова.
Правило 2: при работе с проблемой ключевых слов
должно быть как можно меньше.
Правило 3: наличие множества ключевых слов
предполагает деление проблемы на отдельные
смысловые блоки.
Правило 4: встречающиеся информационные блоки
желательно укрупнять.
Читая текст задания, сосредотачиваем внимание на словах «параметр», «единственное», «целое», а также на встречающихся конструкциях задачи, содержащих квадратный трехчлен и модуль.
Хочу отметить, что до самого окончания работы участники так и не смогли прийти к единой интерпретации условия (см. № 7 мозаики), проблему не решила даже консультация филолога. Комментарии по этому поводу будут приведены ниже.
Приглаживаем «монстра», делаем задачу более обозримой, укрупняем информационные блоки: t(x) = x2 –2x –3, b(a) = (a2 – a/2)/3. Зная t и b, легко возвратиться к x и a. Для этого необходимо и достаточно знать свойства квадратного трехчлена и уметь решать квадратные уравнения и квадратичные неравенства.
Выполнив замену переменных, приходим к
необходимости изучить решение неравенства ![]() Используя схемы
равносильного перехода, отвечающие пункту 18
мозаики, приходим к равносильной системе
неравенств (*):
Используя схемы
равносильного перехода, отвечающие пункту 18
мозаики, приходим к равносильной системе
неравенств (*):
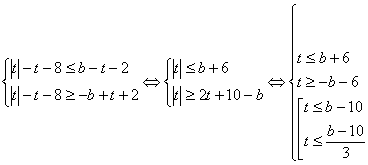 . Для
исследования задачи построим множество точек,
координаты которых удовлетворяют последней
системе на плоскости Obt (Рисунок 1).
. Для
исследования задачи построим множество точек,
координаты которых удовлетворяют последней
системе на плоскости Obt (Рисунок 1).
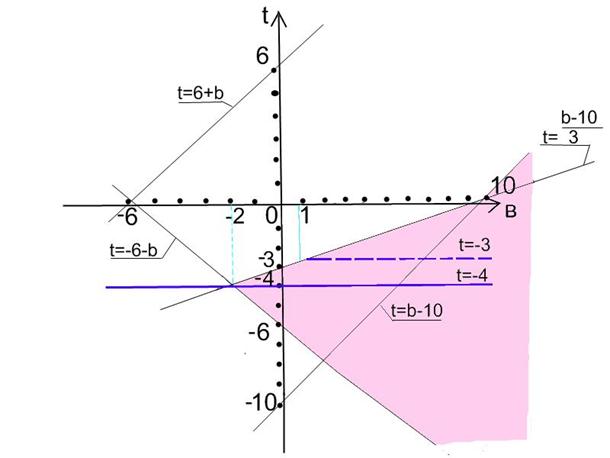
Вернемся к исходной задаче. ![]() Если x0
удовлетворяет исходному неравенству, то
значение 2 – x0 также ему
удовлетворяет. Следовательно, единственным
целым решением неравенства может быть только x0
= 1, при этом t = – 4. Чтобы других целых решений
не было t должно удовлетворять условию t < –
3. Из рисунка следует, что если в число решений
должно входить единственное целое решение, то
нас устраивают все b из полуинтервала [– 2; 1). Если
же у нас решение только одно и оно целое, то b
= – 2.
Если x0
удовлетворяет исходному неравенству, то
значение 2 – x0 также ему
удовлетворяет. Следовательно, единственным
целым решением неравенства может быть только x0
= 1, при этом t = – 4. Чтобы других целых решений
не было t должно удовлетворять условию t < –
3. Из рисунка следует, что если в число решений
должно входить единственное целое решение, то
нас устраивают все b из полуинтервала [– 2; 1). Если
же у нас решение только одно и оно целое, то b
= – 2.
Возвращаемся к переменной a, получаем интервал (–
1.5, 2). Можно отметить, что ни при каких значениях
параметра а единственного решения у неравенства
нет.
Для развития навыков исследовательской работы
учащихся важны открытые вопросы. Представленный
рисунок легко использовать в качестве
генератора семейства задач. Предполагая, что t –
переменная, а b – параметр, легко
сформулировать, например, задачи.
1. При каких значениях параметра b все значения ![]() являются
решениями системы неравенств (*)?
являются
решениями системы неравенств (*)?
2. При каких значениях параметра b система
неравенств (*) не имеет решений?
3. При каких значениях параметра b система
неравенств (*) имеет единственное решение?
4. При каких значениях параметра b хотя бы одно
значение из промежутка [– 2; 1] является решением
системы неравенств (*)?
5. При каких значениях параметра b система
неравенств (*) имеет только отрицательные
решения?
6. При каких значениях параметра b система
неравенств (*) имеет ровно 3 целых решения?
Очевидно, что возможность задания различных
функций t(x) и b(a) делает очень
широким спектр задач, на базе ГМТ на плоскости Obt.
Мы полагаем, что организация занятий, в ходе
которых учащиеся во многом самостоятельно
открывают для себя собственные возможности и
оценивают свои достижения, способствует
становлению их компетентности, понимаемой как
«… способность учащихся самостоятельно
действовать в ситуации неопределенности для
решения актуальных для них проблем". (О.Е.
Лебедев).
Таким образом, развитие учителем критического мышления как мышления оценочного и рефлексивного и создание ситуаций, когда возникает потребность в его использовании, может служить прекрасным средством формирования ключевых компетентностей учащихся.