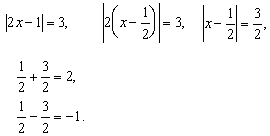Цели:
- Ввести определение модуля действительного числа, рассмотреть свойства и разъяснить геометрический смысл модуля;
- Ввести функцию
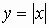 ,
показать правила построения ее графика;
,
показать правила построения ее графика; - Научить разными способами решать уравнения, содержащие модуль;
- Развивать интерес к математике, самостоятельность, логическое мышление, математическую речь, прививать аккуратность и трудолюбие.
Оборудование: проектор, экран, персональный компьютер, мультимедийная презентация
Ход урока
1. Организационный момент.
2. Актуализация знаний учащихся.
2.1.Ответить на вопросы учащихся по домашнему заданию.
2.2. Разгадать кроссворд (повторение теоретического материала) (Слайд 2):
- Комбинация математических знаков, выражающая какое-нибудь
– Разгадав кроссворд, в выделенном вертикальном столбце прочитайте название темы сегодняшнего урока. (Слайды 3, 4)
3. Объяснение новой темы.
3.1. – Ребята, вы уже встречались с понятием модуля, пользовались обозначением |a|. Раньше речь шла только о рациональных числах. Теперь надо ввести понятие модуля для любого действительного числа.
Каждому действительному числу соответствует единственная точка числовой прямой, и, наоборот, каждой точке числовой прямой соответствует единственное действительное число. Все основные свойства действий над рациональными числами сохраняются и для действительных чисел [7].
![]()
Вводится понятие модуля действительного числа. (Слайд 5).
Определение. Модулем неотрицательного действительного числа x называют само это число: |x| = x ; модулем отрицательного действительного числа х называют противоположное число: |x| = – x [2, с. 76].
– Запишите в тетрадях тему урока, определение модуля:
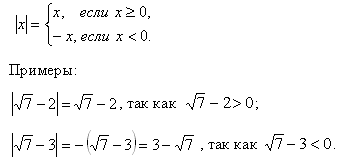
На практике используют различные свойства модулей, например. (Слайд 6) [2, с. 76] :
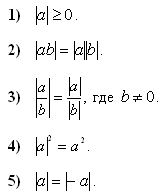
Выполнить устно № 16.3 (а, б) – 16.5 (а, б) на применение определения, свойства модуля. (Слайд 7) [3].

3.4. Для любого действительного числа х можно вычислить |x| , т.е. можно говорить о функции y = |x| .
Задание 1. Построить график и перечислить свойства функции y = |x| (Слайды 8, 9).
Один ученик на доске строит график функции
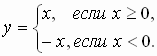
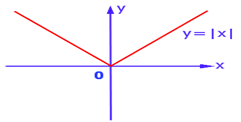
Рис 1. [6]
Свойства перечисляются учащимися. (Слайд 10)
1) Область определения – ( – ∞; + ∞).
2) у = 0 при х = 0; y > 0 при x < 0 и x > 0.
3) Функция непрерывная.
4) унаим = 0 при х = 0, унаиб не существует.
5) Функция ограничена снизу, не ограничена сверху.
6) Функция убывает на луче ( – ∞; 0) и возрастает на луче [0; + ∞).
7) Область значений функции – луч [0; + ∞).
3.5. Разъясняется геометрический смысл модуля. (Слайд 11)
Модуль числа – это расстояние от начала отсчета до данного числа [8].
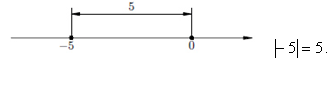
Рис. 2
Числовая прямая есть геометрическая модель множества R действительных числе. Отметим на числовой прямой две точки: a и b (два действительных числа a и b), обозначим через p(a; b) расстояние между точками a и b:
p(a; b) = |a – b| [2]
3.6. Задание 2. Решить уравнение |x – 1| = 4.
– Ребята, какими способами можно решить уравнение?
– Аналитически, графически.
I способ. Один ученик решает уравнение аналитически на доске.
(Слайд 12) По определению модуля имеем:
| х – 1 = 4, х = 5. |
– (х – 1) = 4, х – 1 = – 4, х = – 3. |
Ответ: -3; 5.
II способ. Другой ученик решает данное уравнение графически на доске.
(Слайд 13) Построим на одной координатной плоскости графики функций y = |x – 1| и у = 4. Абсциссы точек пересечения графиков будут решениями уравнения.
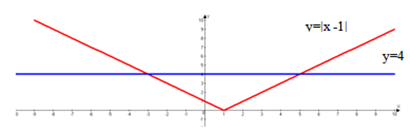
Рис. 3
Ответ: -3; 5.
III способ.
Учитель: – Некоторые уравнения с модулем решаются проще с помощью геометрических соображений. Уравнение формулируется на “языке расстояний”, выполняется чертеж, и из чертежа сразу видно решение уравнения. (Слайд 14).
Уравнение |x – 1| = 4 можно прочитать так: нужно найти на числовой прямой такие точки, которые удалены от точки 1 на расстояние, равное 4.
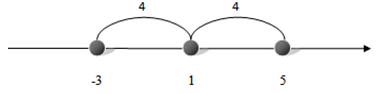
Рис. 4
1 + 4 = 5,
1 + (– 4) = -3.
Ответ: -3; 5.
4. Закрепление нового материала.
№ 16.24 (а, б) решить на “языке расстояний”.
№ 16.29 (а) решить аналитически и на “языке расстояний”. (Слайды15, 16)
I способ. (Слайд 15)
|2x – 1| = 3 по определению модуля имеем совокупность уравнений:
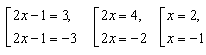
Ответ: -1; 2.
На “языке расстояний” (Слайд 16):
| I способ (а)
Ответ: -1; 2. |
II способ (б) |2x – 1| = 3, На расстоянии 3 от точки 1 лежат две 2х = 4 или 2х = -2, Ответ: -1; 2. |
5. Подведение итогов урока/
Учитель: – Какой способ является наиболее подходящим для решения данных уравнений (Слайд 17)?
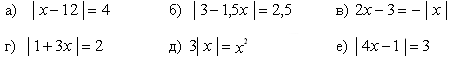
6. Домашнее задание (Слайд 18): прочитать материал §16, №16.8(в), 16.24(в), 16.30(в), 16.38(в), 16.42*(в) [3].
Список использованной литературы:
- Звавич Л.И. Алгебра. Углубленное изучение. 8 кл.: задачник / Л.И. Звавич, А.Р. Рязановский. – 4-е изд., испр. – М.: Мнемозина, 2006. – 284 с.
- Мордкович А.Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений /А.Г. Мордкович. – 12-е изд., стер. – М.: Мнемозина, 2010. – 215 с.
- Мордкович А.Г и др. Алгебра. 8 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / под ред. А.Г. Мордковича. – 12-е изд., испр. и доп. – М.: Мнемозина, 2010. – 271 с.
- Мордкович А.Г. Алгебра. Углубленное изучение. 8 кл.: учебник. – 3-е изд., стер. – М.: Мнемозина, 2006. – 256 с.
- Студенецкая В.Н., Сагателова Л.С. Математика. 8–9 классы: сборник элективных курсов. Вып. 1 / авт.-сост. В.Н. Студенецкая, Сагателова. – Волгоград: Учитель, 2007. – 205 с. http://www.resolventa.ru/spr/algebra/modul.htm – Подготовка школьников к ЕГЭ и ГИА в учебном центре "Резольвента" (Справочник по математике – Алгебра – Модуль действительного числа); http://unichance.ru/pages/32/?uid=607 – Школа математики Unichance. Банк задач – Рациональные и действительные числа
- http://mirurokov.ru/otkrytyi-urok/27-modul-chisla/109-modul-chisla.html – Мир уроков. Модуль числа.