В последнее время многие учителя соглашаются с констатацией педагогов – психологов: настолько широким и привлекательным стало внешнее виртуальное воздействие на учащихся, что информация, подаваемая им на уроках, проигрывает по красочности, значимости, а потому отправляется в неведомые кладовые подсознания, где, зачастую, теряется безвозвратно.
Во многом это затрагивает и многострадальную геометрию. Представляется, что активное использование интерактивных моделей, создаваемых самими учащимися, позволит задержать их внимание на предлагаемых конструкциях, самостоятельно “открывая велосипед”, понять, сколько труда и гения вложено в математическую теорию. Предваряя практическими работами изучение материала на уроках, учитель в классе работает с подготовленной аудиторией и может сосредоточиться на большем числе деталей доказательства и сравнительном анализе.
Созданные же самим педагогом интерактивные модели позволяют экономию пространства и времени перевести в возможность развития приемов критического мышления, исследовательской деятельности и креативности аудитории.
Представленные далее задания выполнялись на базе “Математического конструктора 5.5”, освоение приемов работы в котором позволит создавать модели, похожие на те, что приложены к программе. Но самостоятельная работа учащихся с инструментами, заложенными в программе, намного расширяет круг охватываемых задач и тем, позволяя каждому учителю создавать свою серию практических работ, а также организовывать проектную деятельность учащихся.
Хотелось бы отметить, что спектр заданий, использующих интерактивные модели, весьма широк. Гибкие иллюстрации к материалам учебных занятий, исследование возможности построения фигур с расчетом их элементов, создание тематических практических работ, развитие познавательных интересов учащихся, выполнение проектов, создание банка данных конструкций при подготовке к итоговой аттестации и т.д. Посмотрим, как можно использовать возможности конструктора уже в привычной для учителя ситуации – подготовке учащихся к итоговой аттестации по математике.
Пример №1. Задача 26 ГИА 2014 Математика Тренировочные задания, Москва, ЭКСМО Вариант 7 стр. 47. В трапеции ABCD боковая сторона CD равна m, а расстояние от середины боковой стороны AB до прямой CD равно n. Найдите площадь трапеции.
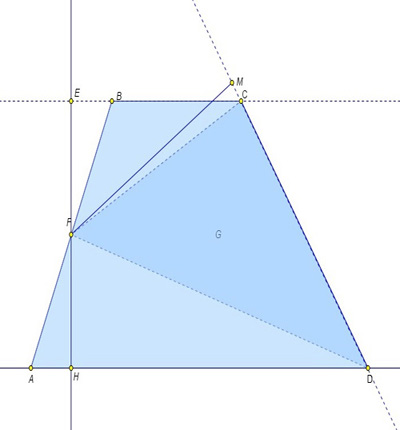
Решение. Пусть т. F – середина стороны AB. Опустим из точки F перпендикуляр на прямую CD, его длина равна n. Докажем, что площадь треугольника CDF равна половине площади трапеции.
1. Проведем через точку F прямую, перпендикулярную AD, так как AD II BC, то
эта прямая перпендикулярна BC. Соответствующие точки пересечения прямых
обозначим H и E. ∆ FEB = ∆ FHA по гипотенузе и острому углу (треугольники
прямоугольные, AH = BF, ![]() EFB=
EFB=
![]() HFA, как вертикальные). Следовательно, FE = FH, а так как расстояние EH между
параллельными прямыми равно высоте трапеции h, то FE = FH = h/2. 2) Площадь ∆
FBC = BC∙h/4, а ∆ AFD = AD∙h/4. 3) Для площади трапеции получаем (AD+BC)∙h/2. 3)
Трапеция ABCD составлена из треугольников AFD, BCF, FCM. Поскольку сумма
площадей двух первых треугольников равна половине площади трапеции, площадь
треугольника FCD также составляет её половину. 4) S∆(FCD) = CD∙FM/2.
Тогда S(ABCD) = mn. Ответ: mn.
HFA, как вертикальные). Следовательно, FE = FH, а так как расстояние EH между
параллельными прямыми равно высоте трапеции h, то FE = FH = h/2. 2) Площадь ∆
FBC = BC∙h/4, а ∆ AFD = AD∙h/4. 3) Для площади трапеции получаем (AD+BC)∙h/2. 3)
Трапеция ABCD составлена из треугольников AFD, BCF, FCM. Поскольку сумма
площадей двух первых треугольников равна половине площади трапеции, площадь
треугольника FCD также составляет её половину. 4) S∆(FCD) = CD∙FM/2.
Тогда S(ABCD) = mn. Ответ: mn.
В данном издании похожие задачи предлагаются во многих вариантах. Для организации повторения темы “Площадь трапеции” или её изучения в 8 классе можно предложить учащимся выполнение практической работы в среде “Математический конструктор 5.5”
Примерный план практической работы “Площадь трапеции” (для начинающих работу в данной программе).
- Постройте две параллельные прямые a и b.
- Отметьте на прямой a точку A, на прямой b точку B.
- Пересеките параллельные прямые третьей прямой с. Отметьте точки пересечения: с прямой a - точку D, с прямой b – точку C.
- Вычислите площадь четырехугольника ABCD.
- Разделите отрезок CD пополам точкой M.
- Проведите через точку деления прямую, пересекающую прямую a в точке D1, а прямую b в точке C1 .
- Найдите площадь треугольника ABM, площадь четырехугольника ABC1D1.
- Поэкспериментируйте с другими трапециями, оставляя неизменной одну из боковых сторон и точку - середину другой боковой стороны.
- Попробуйте сформулировать связь между площадью треугольника ABM и площадью получающихся трапеций.
- Докажите теорему: площадь трапеции равна произведению длины боковой стороны на расстояние от середины другой боковой стороны до прямой, содержащей первую боковую сторону.
Выполняя задания работы, учащиеся могут самостоятельно прийти к выводу, что задание элементов трапеции в условии не определяет её однозначно, а потому не стоит стараться свести решение задачи к нахождению всех элементов трапеции через задающую их систему алгебраических уравнений.
Более сложные задачи на экзамене в 11 классе содержат зачастую несколько стандартных конструкций, которые можно отработать по отдельности. Очень часто в задачах встречаются темы, затрагивающие среднюю линию трапеции.
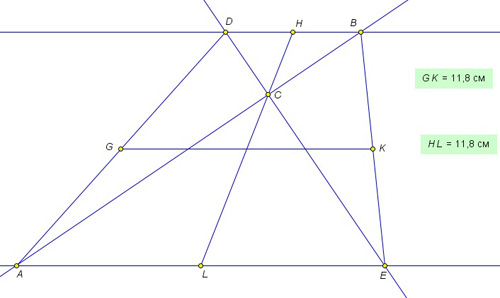
Примерный план практической работы “Средние линии трапеции”.
- Постройте две перпендикулярные прямые, обозначьте их точку пересечения.
- Проведите горизонтальные прямые через точки на одной из них, лежащие по разные стороны от точки пересечения.
- Выбрав точки пересечения горизонтальных прямых с двумя исходными, постройте соответствующую трапецию.
- Разделив боковые стороны трапеции пополам, постройте первую среднюю линию трапеции.
- Разделив основания трапеции пополам, постройте вторую среднюю линию трапеции.
- Измерьте длину средних линий, сравните результаты.
- Повторите моделирование дополнительно для двух других трапеций с перпендикулярными диагоналями.
- Верна ли теорема “Если диагонали трапеции перпендикулярны, то длины её средних линий равны”?
- * Дополнительное задание. Если уж речь заходит о средних линиях, желательно обратить внимание на то, что вторая средняя линия трапеции проходит через точку пересечения диагоналей трапеции, а её продолжение через точку пересечения продолжений боковых сторон.
Пример № 2. ЕГЭ 2014 Математика (под редакцией А.Л. Семенова, И.В. Ященко), издательство АСТ Москва.
Вариант 6. С4 (стр. 79). Две окружности касаются внешним образом в точке К. Прямая касается первой окружности в точке А, а второй – в точке B. Прямая ВК пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C. а) Докажите, что AD II BC. б) Найдите площадь треугольника DKC , если известно, что радиусы окружностей равны 4 и 9.
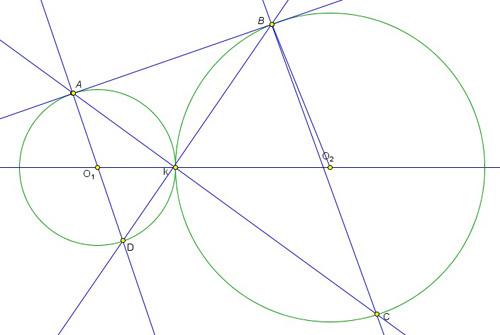
Решение. Пусть O1 и O2 – центры окружностей. Соединим их с точками касания A и B соответственно. O1A и O2B перпендикулярны AB как радиусы, проведенные в точки касания. Кроме того, как два различных перпендикуляра к одной прямой на плоскости они параллельны друг другу. В четырехугольнике O1AB O2 сумма всех внутренних углов 360°. Центры окружностей и общая точка касания K лежат на одной прямой. Сумма центральных углов AO1K и BO2K равна 180°, как внутренних односторонних при параллельных O1A и O2B. Сумма углов BAK и ABK равна 90°, так как они как углы между касательной и хордой равны половине соответствующих центральных углов AO1K и BO2K . Тогда угол AKB – прямой и смежные с ним углы AKD и BKD – прямые. Угол ADK равен углу BAK, как вписанный, опирающийся на ту же дугу, что и AO1K, и равный половине центрального. Угол KBO2 дополняет угол ABK до 90°, а потому равен углу BAK и углу ADK. Из равенства внутренних накрест лежащих углов при прямых AD и BO2 и секущей DB следует параллельность AD и BO2. А так как вписанный угол BKC прямой, то он опирается на диаметр, потому точка O2 принадлежит прямой BC и требуемое утверждение доказано.
К сожалению, многие учащиеся автоматически делают вывод о том, что AD и BC – диаметры, так что на рисунке специально изображен центр второй окружности не принадлежащим отрезку BC.
б) В прямоугольной трапеции ABCD полусумма оснований 13.
Отрезок общей внешней касательной равен
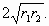 (если из точки O1
опустить перпендикуляр на BC, то получается прямоугольный треугольник с
гипотенузой, равной сумме радиусов окружностей и катетом, равным соответствующей
разности радиусов). Высота трапеции равна 12. Произведение полусуммы оснований
на высоту дает площадь трапеции 156.
(если из точки O1
опустить перпендикуляр на BC, то получается прямоугольный треугольник с
гипотенузой, равной сумме радиусов окружностей и катетом, равным соответствующей
разности радиусов). Высота трапеции равна 12. Произведение полусуммы оснований
на высоту дает площадь трапеции 156.
Для расчета площади заданного треугольника удобно воспользоваться теоремой о разбиении выпуклого четырехугольника диагоналями на треугольники. Эта теорема хорошо ложится для использования её в качестве практической работы.
Примерный план практической работы “Площади четырехугольников”.
1). Постройте выпуклый четырехугольник EFGH.
2) Проведите его диагонали.
3) Вычислите площади получившихся треугольников, одной из сторон которых является сторона четырехугольника.
4) Рассчитайте произведение площадей треугольников с равными вертикальными углами.
5) Повторите работу, изменив исходный четырехугольник. Для этого достаточно, потянув с помощью мыши, изменить положение одной из вершин. Программа автоматически обновит вычисления.
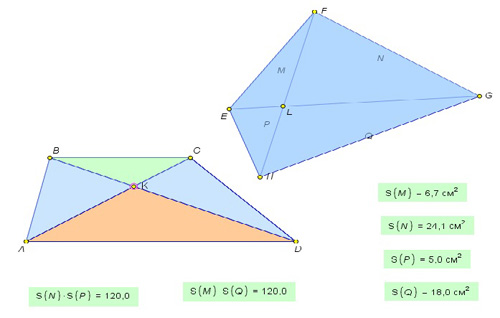
Можно ли утверждать, проведя несколько сравнений, что данное соотношение между произведениями площадей будет справедливо для любого выпуклого четырехугольника?
Как нашу гипотезу превратить в теорему? Для частного случая, когда в качестве выпуклого четырехугольника выбирается трапеция, дополнительно можно при помощи построений убедиться в том, что площади треугольников, примыкающих к боковым сторонам равны, а площади подобных треугольников, примыкающих к основаниям, относятся, как квадраты длин оснований.
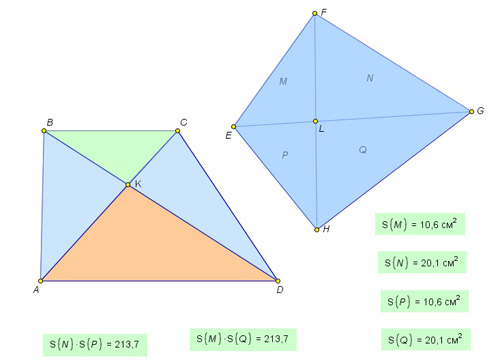
Завершение расчетов примера №2. Если площадь треугольника KBC принять за x, то площадь треугольника KAD равна 16/81x, обозначив площадь треугольника KDC через y, получаем уравнение 16/81x2 = y2, откуда x = 9/4y. Из уравнения для площади трапеции получаем 9/4y+4/9y+2y=156, тогда y= 432/13.
Учителя знают, что зачастую самым сложным для учащихся является составление задачи по мотивам уже решенной. Моделирование задачи в конструкторе помогает понять, какие из условий задачи могут быть избыточными, а каких недостаточно для ответа на вопрос задачи.
Пример конструирования условия. Диагонали трапеции перпендикулярны. На основаниях трапеции, как на диаметрах, построены окружности. Длина отрезка их общей внешней касательной равна 12, а средняя линия трапеции равна 13. Найдите площадь трапеции.
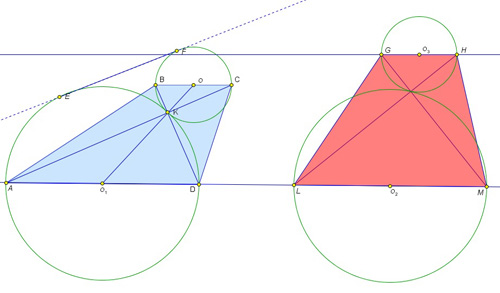
Как видно из сопровождающего рисунка, существует бесконечно
много трапеций, подчиняющихся условию задачи. Радиусы соответствующих
окружностей можно найти из решения системы уравнений
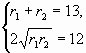 однозначно. Оставляя неизменным
положение большей окружности, мы можем “прокатывать” меньшую окружность так, что
высоты получающихся трапеций меняются, оставляя неизменными основания.
Следовательно, данных задачи для определения площади трапеции недостаточно.
однозначно. Оставляя неизменным
положение большей окружности, мы можем “прокатывать” меньшую окружность так, что
высоты получающихся трапеций меняются, оставляя неизменными основания.
Следовательно, данных задачи для определения площади трапеции недостаточно.
Пример конструирования условия. Диагонали трапеции перпендикулярны. На основаниях трапеции, как на диаметрах, построены окружности. Длина отрезка их общей внешней касательной равна 12, большее основание трапеции равно 16, а средняя линия трапеции равна 13. Найдите площадь трапеции. В приведенном условии исходные данные не только избыточны, но и противоречивы, так что такой трапеции не существует.
Перед изучением теоремы синусов может быть интересной следующая практическая работа.
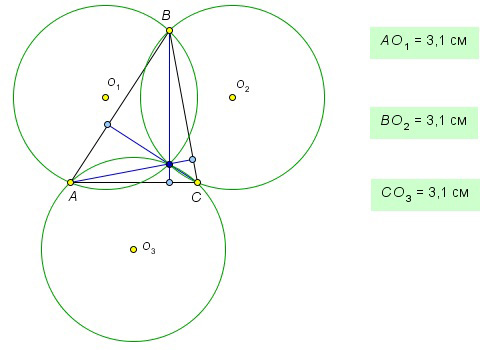
Примерный план практической работы “Описанные окружности”.
- Постройте произвольный остроугольный треугольник, выбрав пункты меню: Мои инструменты – Геометрия треугольника – Треугольник с высотами.
- Постройте три окружности, выбрав в меню Построения – Окружности и дуги – Окружность по трем точкам: две произвольные вершины треугольника и его ортоцентр.
- Измерьте радиусы получившихся окружностей и сравните их.
- Повторите действия для других исходных треугольников, в том числе тупоугольных.
- Проведете окружность через три вершины треугольника, измерьте радиус описанной окружности.
- Сформулируйте гипотезу, которая может появиться после сравнения результатов измерений.
- Попробуйте доказать соответствующую теорему.
Из результатов работы в “Математическом конструкторе” следует, что радиусы окружностей, проходящих через две вершины исходного треугольника и его ортоцентр равны. Последующее сравнение позволяет сделать вывод, что для всех построенных конструкций эти радиусы совпадают по величине с радиусом окружности, описанной около исходного треугольника.
Рассмотрим конструкцию в деталях.
В четырехугольнике DFCE два угла прямые, следовательно,
![]() Тогда
Тогда
![]()
И мы близки к разгадке: из теоремы синусов, которая будет доказана, следует, действительно, радиусы полученных четырех окружностей равны.
В старших классах в качестве задания для любознательных учащихся обычных классов можно предложить практическую работу по мотивам теоремы Наполеона (Доказательство таковой с помощью теоремы косинусов и формул тригонометрии уместно в классах с углубленным изучением математики).
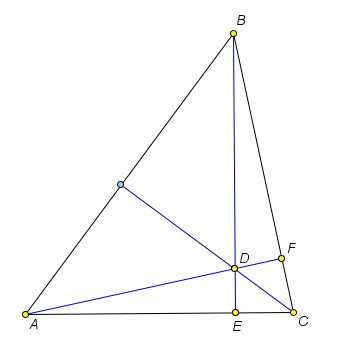
Примерный план практической работы “Теорема Наполеона”.
- Постройте произвольный остроугольный треугольник.
- На его сторонах во внешнюю сторону постройте равносторонние треугольники.
- Найдите их центры.
- Измерьте расстояния между центрами получившихся равносторонних треугольников.
- Каков вид треугольника, вершинами которого являются центры построенных равносторонних треугольников.
- Повторите все действия для тупоугольного треугольника.
- Отложите равносторонние треугольники во внутреннюю сторону остроугольного треугольника.
- Сформулируйте возможную гипотезу по результатам практической работы.
На рисунке ниже представлены иллюстрации к пунктам 6 и 7 практической работы.
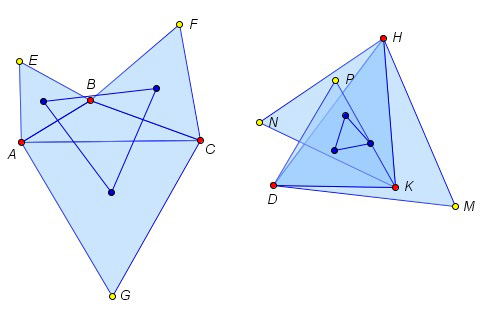
Представляется, что использование “Математического конструктора” будет увлекательным при организации профильных летних смен (это уже проверено на опыте), а также при подготовке учащихся к олимпиадам различного уровня.
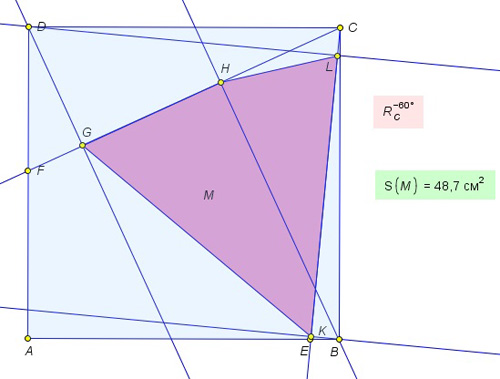
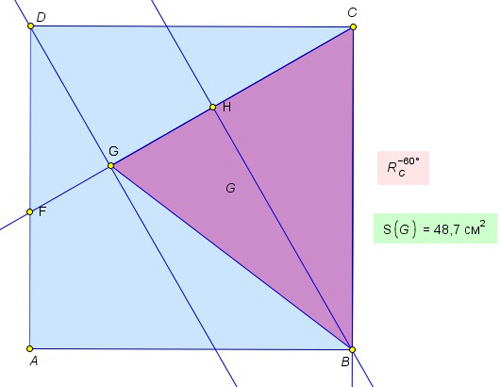
Олимпиадная задача “Физтех 2014” online тур. На сторонах AB и AD квадрата ABCD со стороной a отмечены точки E и F соответственно. Угол ECF равен 60°. Из вершин B и D проведены перпендикуляры к отрезкам CE и CF. Какая наибольшая площадь может быть у четырехугольника с вершинами в основаниях этих перпендикуляров?
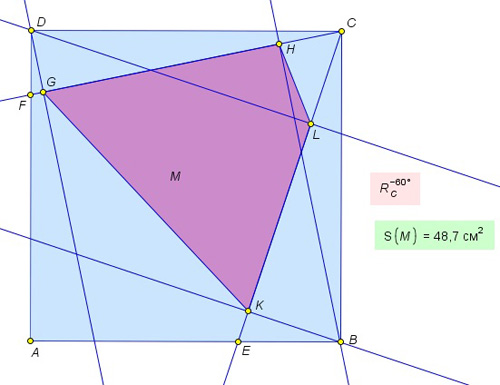
Построения и вычисления в программе “Математический конструктор” показывают, что величина площади многоугольника является инвариантом, причем в случае вырождение четырехугольника в треугольник результат не изменяется. Объяснение происходящему можно найти, если увидеть, что отрезок DC виден из точек G и L под прямым углом, то есть последние две точки лежат на окружности с диаметром DC. Аналогично, точки H и К лежат на окружности с диаметром BC. Диагонали многоугольника искомой площади GL и KH видны из соответствующих точек окружностей под углом 60° и из равенства вписанных углов можно доказать, что они перпендикулярны друг другу. Следовательно, площадь четырехугольника равна половине произведения его диагоналей, от расположения точки Е на стороне квадрата площадь не меняется.