На сайте Г.И. Яркового я обнаружил эту геометрическую головоломку. Широко известная в математике спираль, составленная из подобных треугольников. Её можно накручивать сколь угодно долго, но автор ограничился семью первыми треугольниками, и предлагает сложить их них квадрат!
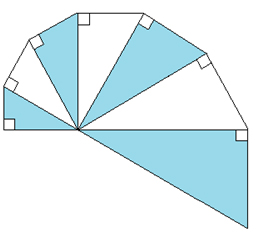
Отношение катетов или величину острых углов треугольников он не указал, а без знания этих величин решать головоломку бессмысленно.
Заинтересовав этой проблемой своих кружковцев, мы принялись за исследование. Первое, что предложили ребята: не складывать квадрат из треугольников, а наоборот, разрезать квадрат на подобные треугольники. И это логично, потому, что параметры подобных треугольников нам были неизвестны.
Во-вторых, заметили, что квадрат легко превращается в прямоугольный треугольник. Для этого достаточно разрезать его на две части прямой, проходящей через вершину квадрата и середину его стороны, и сложить прямоугольный треугольник. Разбиение прямоугольного треугольника на подобные треугольники выполняется делением по высоте, проведенной к гипотенузе. Сделав ещё пять разрезов, получим разбиение треугольника на семь подобных треугольников.
Кажется, что головоломка решена, но ребята выполнили расчеты и …. С одной стороны, пусть АВ = 4, это сторона исходного квадрата. С другой стороны, решая прямоугольные треугольники, можно последовательно вычислить длины отрезков. Длина АВ окажется равной 3,90625, что отличается, хотя и не много, от 4. Возникает противоречие, значит такое разрезание квадрата на треугольники с отношением катетов 2:1 – не верное.
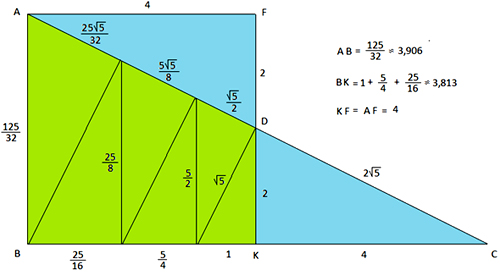
Но какое, же соотношение между катетами в головоломке?
Следующим объектом нашего исследования стали прямоугольные треугольники с углами 30° и 60° градусов. Взяв за основу прямоугольный треугольник с такими углами, разрежем, описанным выше деление по высоте, его на восемь треугольников. Треугольник NKB удалим. Длины сторон всех треугольников нетрудно посчитать, они указаны на рисунке. Квадрирование осуществляется переносом треугольника АВМ на место треугольника CKD. Кажется, что задача решена, но …. Давайте посчитаем!
Меньший катет самого маленького треугольника примем за 1. Тогда вычислив длины АС и СК, замечаем, что АС<СК примерно на 6 тысячных, а ведь эти отрезки должны совпадать при наложении в головоломке. Это говорит о приближенном квадрировании, хотя и лучшем, чем в предыдущем разбиении.
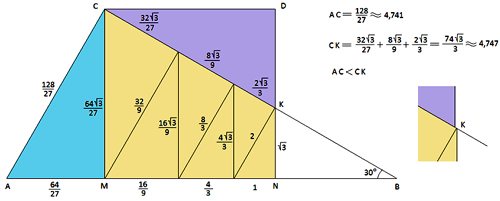
Если посмотреть в увеличительное стекло в районе точки К на рисунке справа, то увидим примерно такую картину. Опять приближенное квадрирование.
А что если “пошевелить” данную систему треугольников. В случае, когда угол треугольников равен 30°, гипотенуза большего треугольника меньше, чем хотелось бы на 6 тысячных. Каким образом ее надо увеличить? Нужно изменить угол, взять не 30° , близкий к нему, Но какой?
Рассмотрим в общем случае. Пусть острый угол треугольников пусть будет равен x радиан, а гипотенуза АС большего треугольника равна 1, тогда решая эти треугольники можно выразить через х стороны всех треугольников. Они указаны на рисунке.

Поскольку АС = СК, то получим тригонометрическое уравнение:
sinxcosx + sinxcos3x + sinxcos5x = 1;
Мы долго мучились, пытаясь решить это уравнение. Но к моему стыду уравнение оказалось для нас неприступным, хотя было много попыток решить это уравнение. Например, заметив, что tgx ≠ 0, можно умножить левую и правую части уравнения, получим sin2x + sin2x cos2x + sin2xcos4x = tgx, но выразив sin2x через cos2x и приведя подобные, получим уравнение cos6x+ tgx = 1. Оно лишь только на первый взгляд простое.
Ещё были попытки решить его через двойной угол, но они тоже оказались тоже неудачными.
Поскольку осилить это уравнение нам не удалось, решили использовать компьютерную программу построения графиков функции, и выяснить существует ли такое значение аргумента х, при котором значение функции у = sinxcosx + sinxcos3x + sinxcos5x принимает значение равное 1.
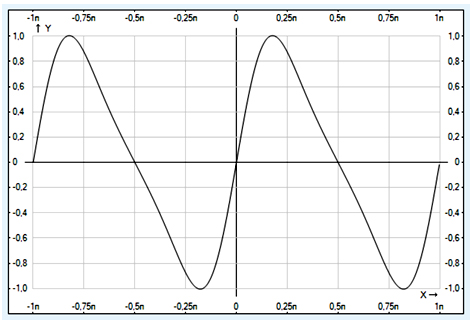
Проанализировав график этой функции, замечаем, что у=1 похоже является экстремальным значением этой функции и принимает она это значение при х ≈ π /6, ведь нас интересует только острый угол. Как найти его точное значение?
Пытались исследовать функцию с помощью производной, но она оказалась громоздкой, и это направление тоже оказалось для нас безуспешным.
Что делать далее? Вспомнили про программирование, уроки информатики и владение языком программирования. На языке TurboBasic написали простенькую программу с использованием цикла. Вот что получилось:
Rem семь треугольников
cls
for x=0.51794 to 0.51795 step 0.000001
y=sin(x)*cos(x)*(1+(cos(x))^2+(cos(x))^4)
print x,y
next x
end
Постепенно сужая промежуток в котором изменяется угол х и увеличивая точность, нам удалось уловить приближенное значение угла х, при котором функция у(х) принимает значение равное 1. Приводим распечатку результатов:
| Угол х | Значение функции у(х) |
| .5179399847984314 . .5179409980773926 .5179420113563538 .5179430246353149 .5179440379142761 .5179450511932373 .5179460644721985 .5179470777511597 .5179480910301208 .5179491043090822 |
.9999979734420776 .9999982118606567 .9999984502792358 .9999987483024597 .9999989867210388 .9999992251396179 .9999995231628418 .9999997615814209 1,000000000000000 1.000000238418579 |
Из приведенной таблицы видно, этот угол равен х ≈ 0.5179480910301208 радиан, и в градусах это х ≈ 29° 40’ 34’’.
Таблица позволяет сделать вывод, что у = 1 не является экстремальным значением, значит есть еще одно значение х, при котором функция у(х) принимает значение равное 1. Заставив работать эту же программу на другом промежутке,
Rem семь треугольников
cls
for x=0.59876 to 0.59877 step 0.000001
y=sin(x)*cos(x)*(1+(cos(x))^2+(cos(x))^4)
print x,y
next x
end
получили следующую таблицу значений:
| Угол х | Значение функции у(х) |
| .5987600088119507
.5987610220909119 .598762035369873 .5987630486488342 .5987640619277954 .5987650752067566 .5987660884857178 .598767101764679 .5987681150436401 .59876912832260132 |
1.000001668930054 1.000001430511475 1.000001072883606 1.000000834465027 1.000000596046448 1.000000357627869 1.00000011920929 .9999998807907104 .9999996423721313 .9999994039535522 |
В таблице находим ещё одно приближенное значение угла х ≈ 0.598766 рад, в градусах это угол х ≈ 34 18’ 24’’. Точного значения угла и в этом случае не найдено, но зато мы теперь точно знаем, что в промежутке острых углов функция у(х) значение 1 принимает дважды при х ≈ 29° 40’ 34’’ и при х ≈ 34 18’ 24’’
Это не очень хорошо видно на приведенном выше графике потому, что линия ведь тоже имеет толщину, а значения функции отличаются от 1 на тысячные доли. Точнее сказать, на приведенном графике этого вообще нельзя увидеть. И только таблица значений функции, полученная с помощью компьютерной программы, позволила нам увидеть, что существуют два угла.
Оказывается, чтобы увеличить гипотенузу самого большого треугольника в таком разрезании, и приблизить её по значению к сумме длин трёх отрезков, угол 30° треугольников можно не только уменьшать, но и увеличивать! Жаль, что мы не смогли найти точные значения этих углов!
Если бы удалось решить уравнение sinxcosx + sinxcos3x + sinxcos5x = 1 , то можно было бы сформулировать и интересную, на мой взгляд, задачу примерно такого содержания: Квадрат сложен из семи подобных треугольников (картинка предлагается). Найдите острый угол этих треугольников.
Ведь часто в сборниках предлагают решить трудное тригонометрическое уравнение, непонятно как появившееся на свет, а здесь-то видно всё как на ладони, как рождается новое тригонометрическое уравнение. Но мы этого сделать не смогли, поэтому задача не получилась! А жаль!
Но если задача не получилась, что же с головоломкой. Мы с кружковцами с вдохновением пытались разобраться во всех тонкостях этой интересной головоломки, и пришли к выводу, что автору не надо переживать насчет приближенного решения. Самое главное такой угол есть, и их даже два. А каково его значение в головоломочном варианте, 30° или 29° 40’ 34’’, совершенно не важно, потому, что отличить их на практике совершенно невозможно.
Проведенные расчеты с помощь компьютерной программы показывают, что острый угол этих подобных треугольников может варьироваться от 29° до 35°, то есть диапазон достаточно широк, и все такие углы можно использовать в головоломке. Погрешности, возникающие при этом будут незаметны в игре с головоломкой.
Пообщавшись в Москве с автором головоломки на ежегодной декабрьской встрече всероссийского клуба ценителей головоломок “Диоген”, я выяснил следующее. Г.И. Ярковой живет г. Тольятти, страстный любитель головоломок, придумал и собственноручно изготовил много оригинальных головоломок. Он – не профессиональный математик, как говорят, любитель занимательной математики, и является трехкратным чемпионом России по решению головоломок в заочном первенстве.
Исследуемая нами головоломка – одно из его творений. Головоломка производится на московском предприятии “Планета головоломок” в двух вариантах: из дерева или из пластика. Её можно купить на сайте. Партия этих головоломок уже продана в Японии. Головоломка называется “7 в квадрате”, так как в начальной позиции из четырех элементов выкладывается цифра “семь”.

Автор любезно подарил мне пластиковый вариант головоломки. Привожу красивые фотографии начального и конечного состояний головоломки. Надо отметить еще один выигрышный ход производителей головоломки – они раскрасили треугольники в два цвета с чередованием. В этом случае и цифра “7” отчетливо выделяется, и конечное решение становится красивым по цветовой гамме. Творческий подход!!
Ну а какой острый угол подобных треугольников в головоломке? Это уже ни кому не важно! Головоломка живет своей жизнью, распространяется по всему миру, потому, что с ней Ярковой Г.И. участвовал в обмене на международной встречи любителей головоломок.