1. Метод проведения вспомогательной окружности.
Проведение вспомогательной окружности около четырехугольника позволяет установить равенство вписанных углов, либо использовать свойства четырехугольника, вписанного в окружность и свойства описанной окружности.
Задача 1. В треугольнике АВС проведены биссектрисы из вершин А и С. Пусть К и L – основания перпендикуляров, опущенных из вершины В на эти биссектрисы.
Докажите, что прямая КL параллельна АС. [3]
Задача 2. Внутри острого угла,
равного ![]() ,
взята точка М, удаленная от сторон угла на
расстояния k и n.
,
взята точка М, удаленная от сторон угла на
расстояния k и n.
Найти расстояние от вершины угла до точки М. [3]
Задача 3. Дан остроугольный треугольник АВС. На сторонах АВ и ВС во внешнюю сторону построены равные прямоугольники АВМN и LВСК так, что АВ = КС.
Докажите, что прямые АL, NК и МС пересекаются в одной точке. [3]
Задача 4. В треугольнике NMF
медиана МА делит угол М так, что ![]() NMА = 20° и
NMА = 20° и ![]() АMF= 30°. Из точки А опущены
перпендикуляры АК и АС на стороны NM и MF
соответственно.
АMF= 30°. Из точки А опущены
перпендикуляры АК и АС на стороны NM и MF
соответственно.
Вычислить площадь треугольника АКС, если АК = 5 и КС = 7. [2]
Задача 5. Пусть А1 , В1 , С1 – точки касания вписанной окружности остроугольного треугольника АВС со сторонами ВС, АС, АВ соответственно. Обозначим через Н1 и Н ортоцентры треугольников ВС1А1 и СА1В1 соответственно.
Доказать, что четырехугольник ВН1НС - вписанный. [3]
2. Применение теоремы Птолемея
Теорема Птолемея: В любом вписанном четырехугольнике произведение диагоналей равно сумме произведений противоположных сторон, т.е. АС•ВD=AB•CD+BC•AD.
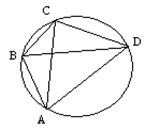
Задача 1. В окружность вписан равнобедренный треугольник АВС (АВ = ВС). На дуге АВ взята произвольная точка К и соединена хордами с вершинами треугольника.
Доказать, что АК • КС = АВ2 – КВ2. [3]
Задача 2. Длины катетов прямоугольного треугольника равны а и в. На его гипотенузе во внешнюю сторону треугольника построен квадрат, одна из сторон которого совпадает с гипотенузой.
Найдите расстояние от вершины прямого угла треугольника до центра квадрата. [3]
Задача 3. В равнобочной
трапеции основание АD равно диагонали АС.
Известно, что ![]() САD
=
САD
= ![]() СDМ, где М –
середина ВС.
СDМ, где М –
середина ВС.
Найти углы трапеции. [1]
Задача 4. Вокруг равностороннего треугольника АВС описана окружность радиуса R и на дуге ВС окружности взята точка М так, что дуга ВС делится этой точкой в отношении 1:3, считая от вершины В.
Найти расстояние АМ. [1]
Задача 5. Доказать, что в равнобочной трапеции произведение длин оснований равно разности квадратов диагонали и боковой стороны. [2]
Используемая литература
1. И.Ф. Шарыгин. Факультативный курс по математике для 10 кл. М., Просвещение, 1989 г.
2. О.Ю. Черкасов. Планиметрия на вступительном экзамене, “Московский лицей”, 1996г.
3. Задачи математических конкурсов и олимпиад 2007-2010 гг.