Профиль класса: физико-математический
Тип урока – повторительно-обобщающий, 45 мин.
Цели урока:
- Закрепить понятия по теме “Метод координат”.
- Развивать умение применять формулы простейших задач к решению примеров.
- Воспитывать культуру корректно отвечать определения и формулы, аккуратно оформлять записи в тетрадях.
Ход урока
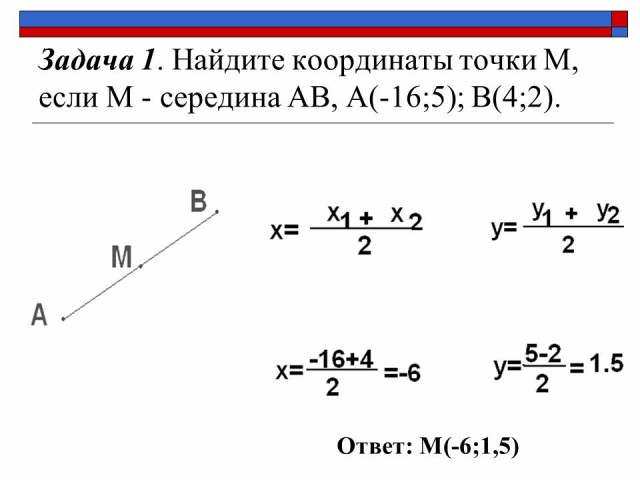
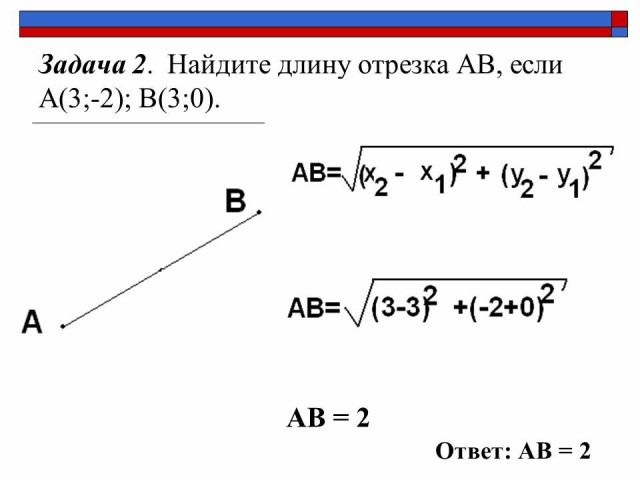
| Организационный этап 1.1. Взаимное приветствие учителя и учащихся 1.2. Сообщение темы и цели урока. 1.3. Настрой на урок. Цель: Выяснить у ответственных учеников о готовности учащихся к уроку. II. Проверка домашнего задания: №902; №1000а; №1044а; 1041а. Слайды № 3- №4; |
2 мин. Слайд № 1 3 мин. |
| №900. Дано: Доказать: Доказательство: 1) d= AB= 2) AC= 3) BC= Так как AB=AC, то Ответ: №1000. Дано: (x-1)2+(y-2)2=25 Выяснить: Является ли это уравнение уравнением окружности, если “да”, то найти координаты центра и радиус окружности. Решение: Так как уравнение имеет вид: (x-x0)2+(y-y0)2 = R2, где (x0;y0) - координаты центра; R - радиус окружности, (1;-2) - координаты центра, R2=25; R2=5 Ответ: R=5; (1;-2) – координаты центра данной окружности. №1041. Дано: Найти: Решение:
Ответ: №1044(а). Дано: Найти: Решение:
Ответ: -2,5 |
|
| III. Повторительно-обобщающий этап:
а) “Из истории возникновения и развития метода координат”. Приготовил: Патрашкин Егор. Историческая справка Первоначально идея координат зародилась в древности в связи с потребностями астрономии, географии, живописи. Так, на стене одной из древнеегипетских погребальных камер была обнаружена квадратная сетка (палетка), которой пользовались для увеличения изображений Древнегреческий астроном Клавдий Птолимей применил географические координаты для определения местонахождения мореплавателя. Идеей координат пользовались в середине века для определения положения светил на небе, для определения места на поверхности Земли. Прямоугольной сеткой пользовались художники эпохи Возрождения. Применять координаты в математике впервые стали Ферма и Декарт. В 1637 году вышла книга Декарта Рассуждения о методе, в которой наряду с общими философскими рассуждениями о материи значительное место уделяется универсальной математике. Декарт предложил новый метод координат, который позволил переходить от точки к паре чисел,
Заслуга Декарта состояла в том, что он ввел переменные координаты. Так, в уравнении ах + ву = с, буквы х и у стали рассматриваться не как неизвестные, а как переменные. О методе координат Метод координат позволяет строить графики уравнений, изображать геометрически различные зависимости, выраженные аналитически с помощью уравнений и формул, решать различные геометрические задачи с помощью алгебры. Термины абсцисса, ордината были введены в употребление Г. Лейбницем в 70, 80-е годы XVII в. б) Презентация задач и решений этих задач по данной теме.
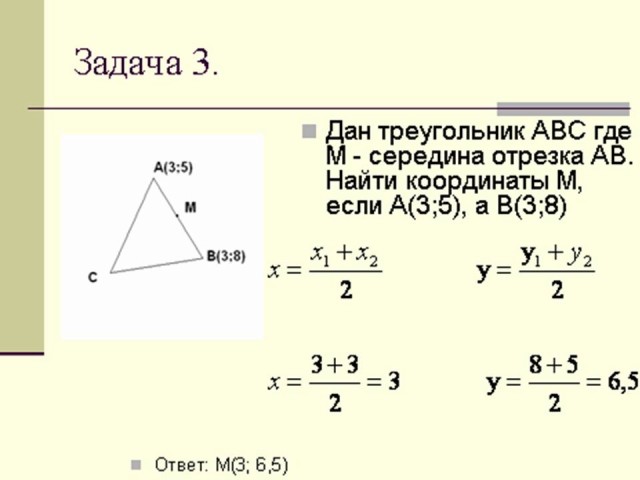
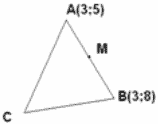
Выполнил Путрин Антон: Дан треугольник ABC, где M – середина отрезка AB. Найти координаты M, если A(3;5), а B(3;8). Ответ: M (3;6,5) |
5 мин. Слайды №5- №9
5 мин. Слайд № 10 Слайд №11 Слайд № 12 |
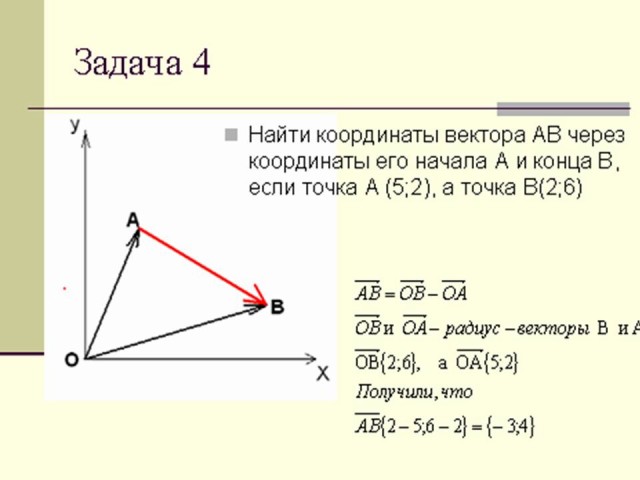
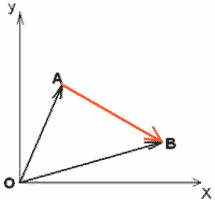
| Задача 4: Выполнила Волкова
Алена Найти координаторы вектора AB через координаты его начала A и конца B, если точка A(5;2), а точка B(2;6).
Получили, что Проекты приготовили ученики дома, защищали на уроке, получили оценки. |
Слайд № 13 |
| IV. Опрос теории. Опрашивается каждый ученик с места, затем проверяются ответы с помощью слайдов. Опрошен каждый ученик:(12 человек: фронтальный опрос, 12 человек: взаимноопрос)
|
7 мин. Слайды № 13- № 17; |
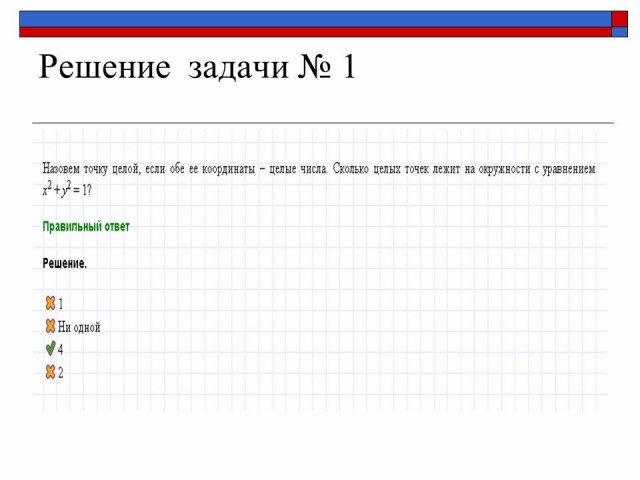
| V. Решение задач. Задания взяты из ЦОР “ Открытая математика 2.6” Планиметртия. Физикон.: Задача №1.
Задача №2.
Задача №3.
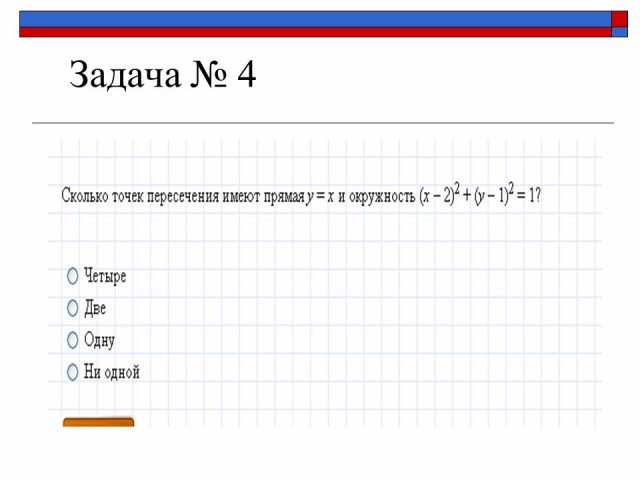
Задача №4.
Задача №5.
|
8 мин. Слайды №19- №28; |
| VI.Самостоятельная работа, состоящая
из заданий А, В, С на два варианта. За любые 4 верно
выполненные задания ставилась оценка “3”; За любые 5 верно решенных задания - оценка- “4”; за 6 верно решенных задания – оценка - “5”. |
10 мин Слайд № 29. |
VII. Итог урока: По результатам
проверочной работы получили:
Всего писали работу 25 человек в 9 а классе. Работа проверялась на уроке по мере поступления на стол учителя. VIII. Домашнее задание: п.86-92 и п.101- 104; №1045; 1004. Консультация по решению.
|
3 мин. 2 мин. Слайд № 30. |
Список литературы:
- Л.С. Атанасян. Геометрия 7-9. М. Просвещение. 2002 г.
- Л.С. Атанасян. Изучение геометрии в 7, 8, 9 классах. Пособие для учителя. М. просвещение. 2000 г.
- ЦОР, Программы Физикона. Открытая математика 2.6. Планиметрия.
- Интернет. Сайт: WWW.MK. RU для учеников 10-11 классов.