В работе предлагаются решения сложных заданий (№15 - №21) ЕГЭ-2015 по математике профильный уровень. Представленный здесь материал предназначен для подготовки к ЕГЭ учащихся, имеющих навык в решении заданий подобного уровня сложности. Задания №15, №16, №17 могут быть предложены сильным учащимся обычных классов, а вот задания №18, №19, №20, №21 целесообразно решать только с учащимися физико-математических классов, причем №21 под буквой “в” под силу только тем, кто имеет определенную подготовку в решении олимпиадных задач.
Для оформления решений использована мультимедиа презентация, где материал, представлен наглядно в ярком, интересном и доступном виде, что для учителя и учащихся будет ценно и полезно. Эту презентацию можно применять как на уроке, так и для индивидуальной работы.
Условия заданий
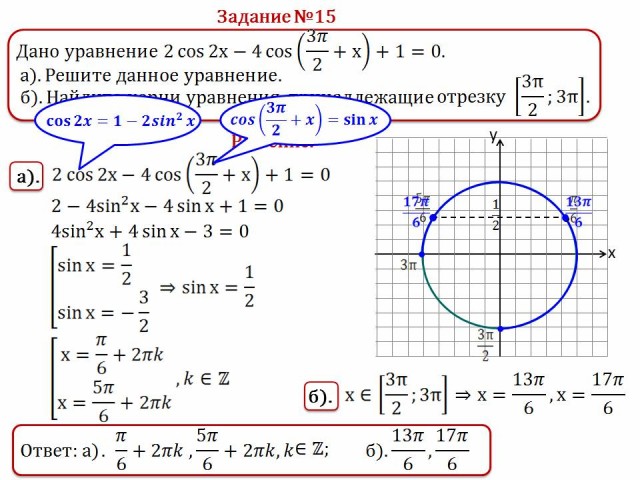
№15.
![]()
а) Решите данное уравнение.
![]()
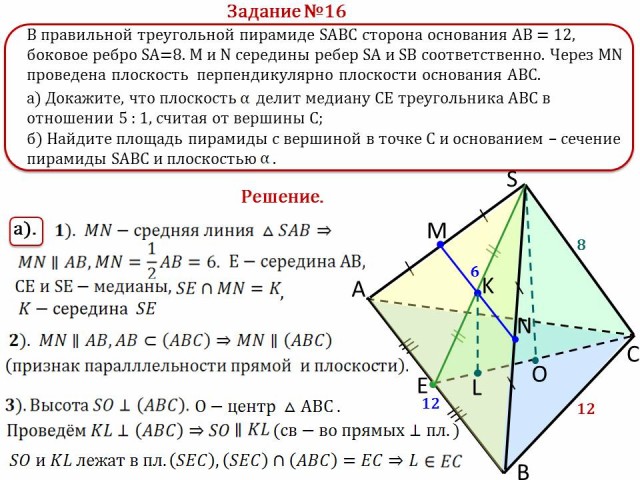
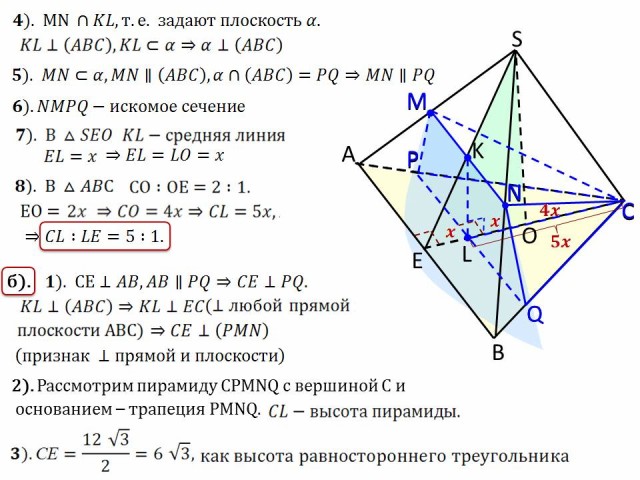
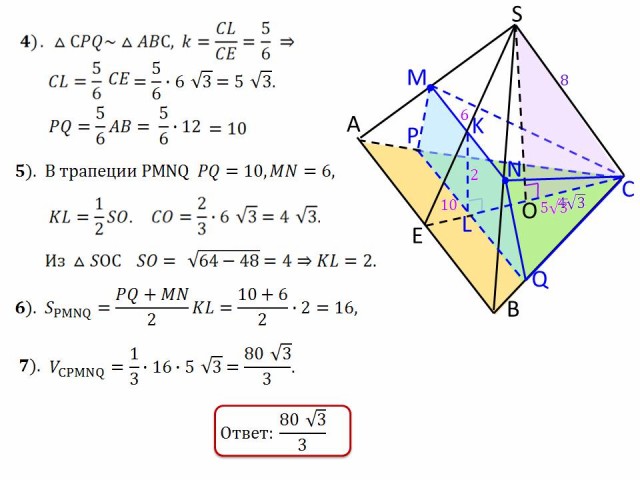
№16.
В правильной треугольной пирамиде SABC сторона
основания АВ = 12, боковое ребро SA = 8. M и N середины
ребер SA и SB соответственно. Через MN проведена
плоскость ![]() перпендикулярно плоскости основания
АВС.
перпендикулярно плоскости основания
АВС.
а) Докажите, что плоскость ![]() делит медиану СЕ
треугольника АВС в отношении 5 : 1, считая от
вершины С;
делит медиану СЕ
треугольника АВС в отношении 5 : 1, считая от
вершины С;
б) Найдите площадь пирамиды с вершиной в точке С
и основанием – сечение пирамиды ABCD с плоскостью ![]()
№17.
![]()
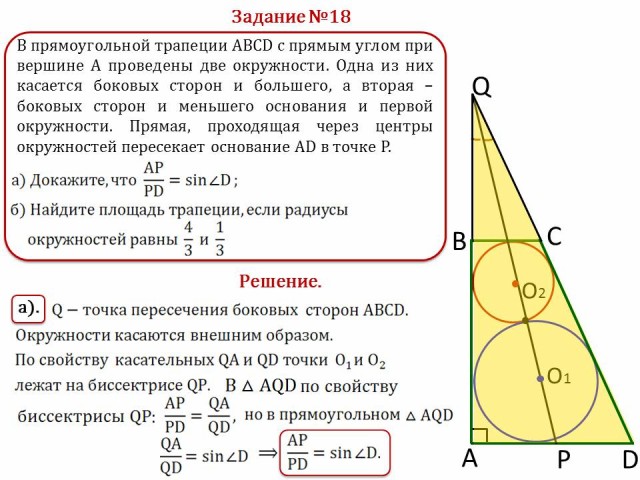
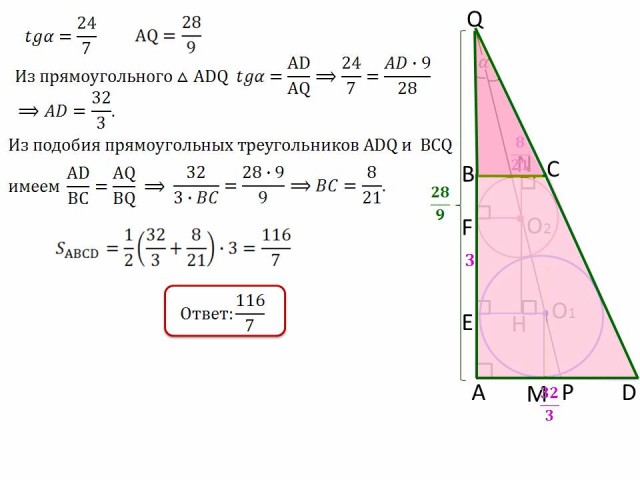
№18.
В прямоугольной трапеции ABCD с прямым углом при вершине А проведены две окружности. Одна из них касается боковых сторон и большего, а вторая – боковых сторон и меньшего основания и первой окружности. Прямая, проходящая через центры окружностей пересекает основание AD в точке Р.
![]()
![]()
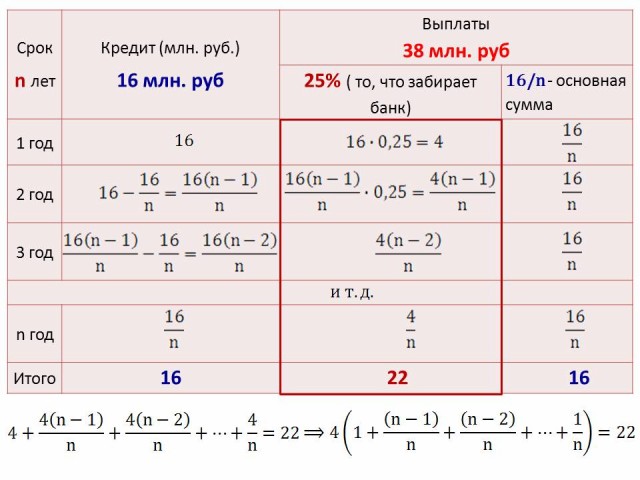
№19
В июле планируется взять кредит в банке на сумму 16 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат его полного погашения составит 38 млн. рублей.
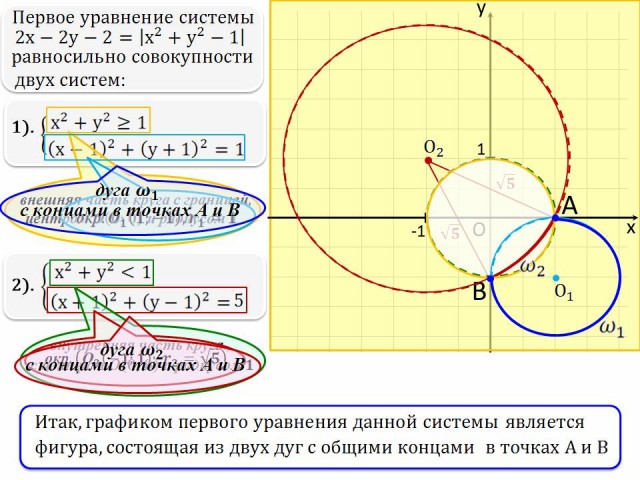
№20.
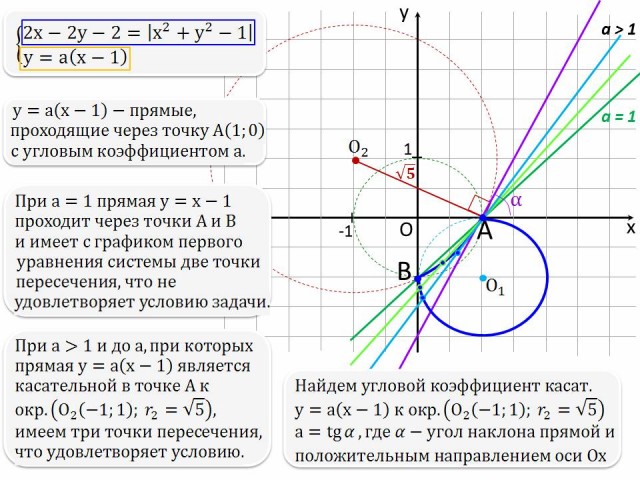
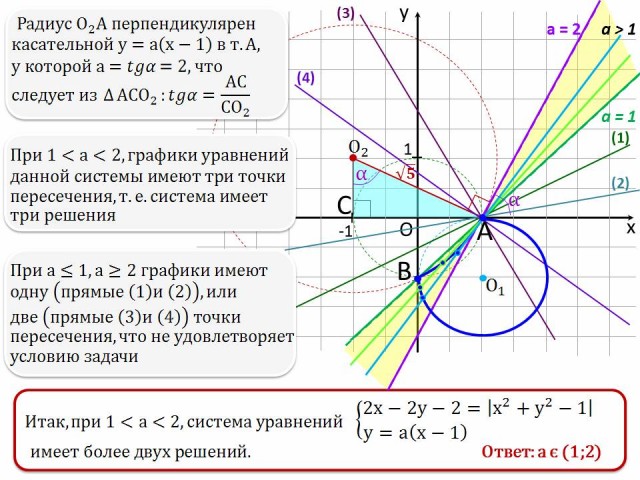
Найдите все значения параметра а, при каждом из которых система уравнений
![]()
Решение заданий № 15-№20 оформлены в презентации.
№21.
На доске было написано 30 натуральных чисел необязательно различных, каждое из которых не превосходит 40. Среднее арифметическое написанных чисел равнялось 7. Вместо каждого из чисел на доске написали число, в два раза меньше первоначального. Числа, которые после этого оказались меньше 1, с доски стёрли.
а) Могло ли оказаться так, что среднее арифметическое чисел, оставшихся на доске больше 14?
б) Могло ли среднее арифметическое оставшихся на доске чисел оказаться больше 12, но меньше 13?
в). Найдите наибольшее возможное значение среднего арифметического чисел, которые остались на доске.
Решение.
а) Пусть на доске было 24 числа, равных 1 и 6 чисел равных 31. Их среднее арифметическое
![]()
![]()
![]()
По условию задачи оказались стёртыми только числа, получившиеся из 1, поэтому
![]()
![]()
Получили, что таких целых k нет.
![]()
![]()
![]()
Пусть А будет наибольшим, если k будет принимать наибольшее возможные значение. Оценим это значение. Каждое из первоначально написанных на доске чисел было не более 40 и на доске осталось 30 – k чисел, поэтому для суммы S выполняется неравенство
![]()
Приведем пример. Пусть первоначально было 25 единиц и 5 чисел равных 37. Их среднее
![]()
![]()
Ответ: а) да; б) нет; в) 18,5