ПОДПИСКА

Цветной журнал с электронными приложениями
Бумажные и электронные версии
Скидки для постоянных подписчиков

№14 – в подарок! Пожалуйста, ознакомьтесь с одним номером.
Вы можете скачать его бесплатно.

Графики уравнений, содержащих знак модуля

Сырцова Светлана Викторовна, учитель математики и информатики

Статья отнесена к разделу: Преподавание математики

Цель:

закрепить методы построения графика линейной функции,
закрепить умение учащихся задавать уравнением функцию, заданную при помощи графика,
познакомить учащихся с тем, каким образом влияет знак модуля на отображение графика линейной функции

Оборудование: презентация (приложение 1)

Ход урока №1

При решении многих математических задач необходимо быстро и точно строить графики любых функций, изучаемых в школьном курсе алгебры. Т.к. на уроке предстоит много построений, начинаем, вспоминая, как строить график линейной функции y = kx + b на основе анализа углового коэффициента и коэффициента смещения (слайд 2)

Сопоставляем уравнения и графики (слайд 3):

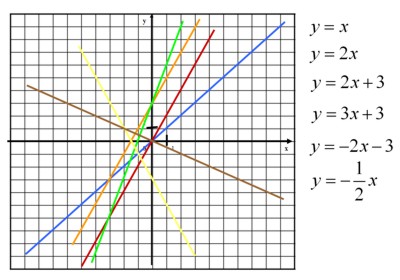
Построим в тетрадях в одной системе координат графики функций (y = -x; y = -x -4; y = -1/3 x – 2; y = 2x + 5; y = x + 1), проверяя себя при помощи слайда 4

Вспомним определение модуля числа x (слайд 5)

Рассматриваем, как можно построить график функции y = |x| на основании определения модуля, отбрасывая части прямых, не лежащих в полуплоскостях x < 0 и x> 0 (слайд 6)

Аналогично рассматриваем способ построения графика функции y = |x + 1| (слайд 7)

Сравнивая графики и уравнения функций (слайд 8-9),

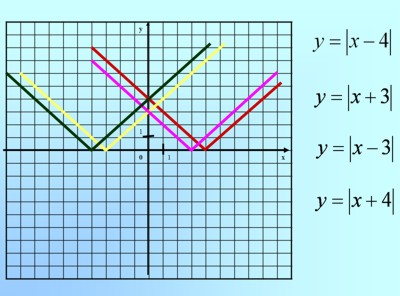
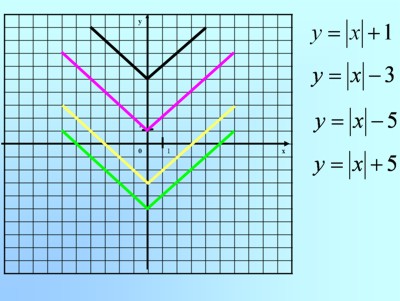
делаем вывод о том, как можно построить график функции y = |x + a| - b смещением графика функции y = |x| (слайд 10-11)

Строим в тетрадях графики функций y = |x-3| + 3, y = |x – 3| - 2, y = |x+2| - 5, y = |x + 3| + 2 и проверяем себя при помощи слайда 12

Далее учащиеся должны на основе рисунка, представленного на слайде 13, задать функцию уравнением:

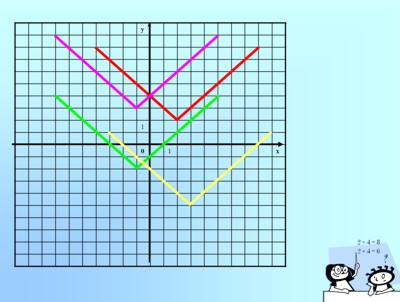
При построении графиков очень важно научить ребят анализировать область определения и множество значений функции и “переносить” указанные множества на координатную плоскость.

Заполняем таблицу (слайд 12):

D(y) E (y)

y = |x|

y = |x – 3|

y = |x – 3| +2

y = - |x|

y = |x + 2| -5

y = - |x +2| -5

И рассматриваем, как множества значений можно определить на основе графиков (слайд 15)

Учащимся предлагается определить D (y) и E(y) по рисунку (слайд 16):

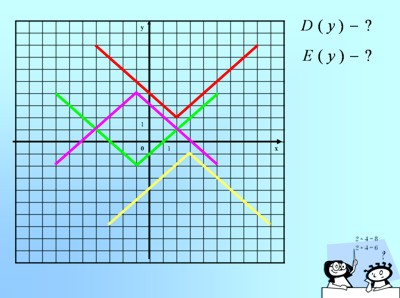
img5.jpg (36657 bytes)

Ученики самостоятельно придумывают уравнение функции по заданным D(y) и E(y) (слайд 17):

Анализируя графики и уравнения (слайд 18), ученики делают вывод о том, как влияет знак минуса перед модульными скобками на график. И самостоятельно задают уравнение по графикам, представленным на слайде 19.

Ход урока № 2

Устно проговариваем уравнения функций по графикам (слайд 20):

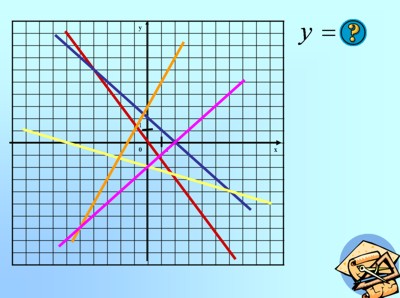
Аналогично схеме предыдущего урока (слайд 21-27) ученики знакомятся с тем, каким образом влияет коэффициент перед аргументом функции на график. В результате они должны научиться описывать уравнением следующие графики:

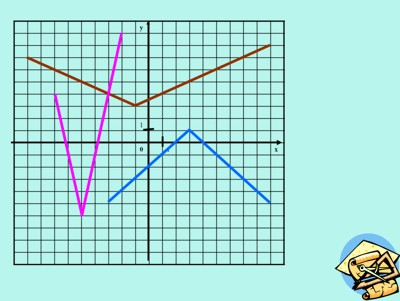
Для закрепления полученных знаний, в тетрадях в одной системе координат ребята строят следующие графики:

y = |0,5x| при -3 < x< 3;

y = 3 при -1 < x< 1;

y = -|x + 3| + 6 при -4 < x < -2;

y = -|x - 3| + 6 при 2 < x < 4;

y = |x + 3| + 4 при -4 < x < -2;

y = |x - 3| + 4 при 2 < x ? 4;

y = -|0,5x – 1,5| + 7 при -5 < x < -1;

y = -|0,5x + 1,5| + 7 при 1 < x < 5.

Проверяют себя по слайду 29:

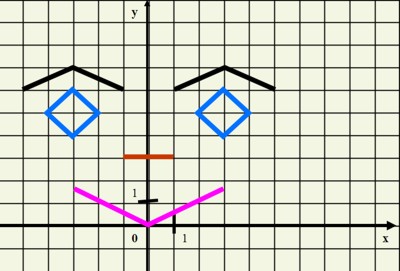
Домашнее задание: придумать картину, состоящую из отрезков прямых, и описать ее при помощи уравнений функций.

Ход урока № 3

Построим графики функций y = |3x| - 3 и y = |3x – 3|. Как в каждом случае связаны y(x) и y(-x)?

Наличие условия y(x) = y(-x) означает симметрию относительно …?

Приведите примеры уравнений функции, графики которых будут симметричны относительно оси ординат

Если в модульные скобки заключается переменная y, то мы получаем условие |y| = |-y|. Какую симметрию задает это условие?

На слайде 34 последовательно рассматриваем цепочку построения графиков:

y = 3x – 3, |y| = 3x – 3, |y| = |3x| - 3, |y| = |3x – 3| путем преобразований симметрии.

Выводим и запоминаем три правила:

Распределите, к какому типу из трех (y = f(|x|, |y| = f(x), y = |f(x)|), можно отнести каждое уравнение:

|y| = 2 – x, y = |3x - 4|, |x| + |y| = 2, |y| = 3x – 4, y = |3|x| - 4|, y = |3x| - 4, |y| = |3|x| - 4|, |y| = |3x – 4|.

Проверяем себя (слайд 35)

Строим последовательную цепочку графиков (тонкими линиями в тетрадях):

1) y = 3x – 4, y = |3x – 4|, y = |3|x| - 4|, |y| = |3|x| - 4|

2) y = 3x – 4, y = 3|x| - 4, y = |3|x| - 4|

Рассматриваем способ построения графика соответствия |x| + |y| = 2.

Самостоятельно строим график |x| - |y| = 2 и проверяем себя по слайду 39.

Домашнее задание: придумать пять уравнений соответствий с модулем, в которых встречаются все случаи, рассмотренные на уроке, и построить графики.