Уравнениями с параметром называются уравнения, у которых коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами.
Решить уравнение с параметром – это значит:
а) исследовать, при каких значениях параметров уравнение имеет корни и при каких не имеет;
б) выяснить количество корней при различных значениях параметров;
в) найти все выражения для корней.
Уравнения с параметром весьма различны по структуре:
Моя работа посвящена отысканию метода решения уравнений с параметрами вида
F(xn; p2) =0
В основе этого метода лежит взгляд на параметр, как на переменную, т.е. уравнение F(xn;p?)=0 можно рассматривать как квадратное относительно параметра р.
Задача 1. Пусть нужно решить уравнение с параметром
![]()
Преобразуем данное уравнение
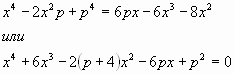
Это уравнение 4-й степени относительно х, причём
содержит ![]() и
и ![]() . Как его решить?
Но заметим, что это уравнение является
квадратным относительно
. Как его решить?
Но заметим, что это уравнение является
квадратным относительно ![]() , т.е. вида
, т.е. вида ![]() . Применим наш метод:
. Применим наш метод:
1. Перепишем уравнение в виде
![]() , т.е.
рассмотрим его как квадратное относительно
, т.е.
рассмотрим его как квадратное относительно ![]() .
.
2. Найдем корни уравнения по формуле корней квадратного уравнения:
![]()
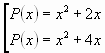
3. Далее используем графический метод. В системе
координат ![]() построим параболы
построим параболы ![]() ,
, ![]() и
и ![]() ,
, ![]()
4. Найдём точки пересечения графиков функций. Для этого приравняем
![]() , отсюда
, отсюда ![]() , т.е. точка
пересечения единственная
, т.е. точка
пересечения единственная ![]() .
.
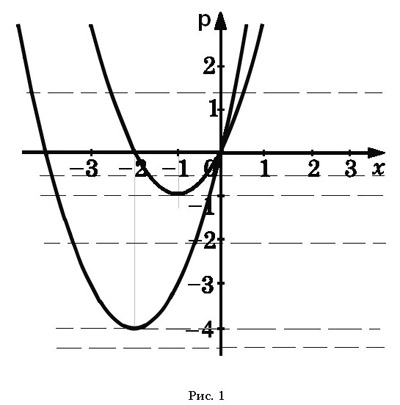
5. По рисунку видно, что горизонтальная прямая
не имеет общих точек с параболами, если она
проходит ниже ![]() , т.е.
, т.е.
при ![]() данное
уравнение не имеет корней
данное
уравнение не имеет корней
при ![]() уравнение имеет единственный корень
уравнение имеет единственный корень ![]()
при ![]() уравнение имеет два корня
уравнение имеет два корня ![]() т.к. прямая имеет две точки
пересечения с параболой
т.к. прямая имеет две точки
пересечения с параболой ![]() , отсюда
, отсюда ![]() ,
, ![]() ,
, ![]()
при ![]() и
и ![]() - три корня
- три корня
при ![]()
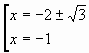
при ![]()
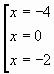
при ![]() и
и ![]() уравнение
имеет четыре корня
уравнение
имеет четыре корня 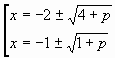
Этот метод не является универсальным, но во многих случаях является весьма результативным и позволяет решать уравнения повышенной сложности, второй степени и выше.
Задача 2. Определить число корней уравнения в зависимости от параметра а х4-10х3-2(а-11)х2+2(5а + 6)х +2а + а2 =0 (1)
Решение. Уравнение является квадратным
относительно параметра а. Перепишем (1) в виде ![]() (2)
(2)
Найдём дискриминант
![]()
Решая уравнение (2), находим
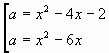
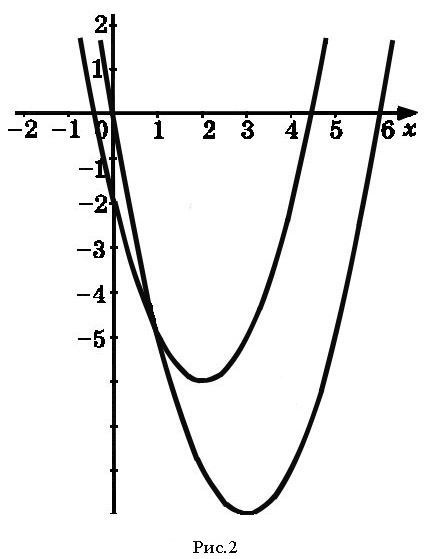
Построим в системе координат (х; а) графики
функций ![]()
и ![]() (рис 2)
(рис 2)
Найдем точки пересечения графиков функций. Для
этого приравняем ![]() отсюда
отсюда ![]() . Далее рассуждая аналогично, как и в
задаче 1, получим
. Далее рассуждая аналогично, как и в
задаче 1, получим
Ответ: если ![]() , уравнение корней не имеет;
, уравнение корней не имеет;
если ![]() один
корень;
один
корень;
если ![]() ,
уравнение имеет два корня;
,
уравнение имеет два корня;
если ![]() три
корня;
три
корня;
если ![]() -
четыре корня.
-
четыре корня.
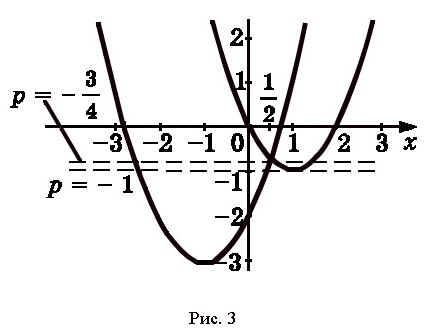
Задача 3. Найти все значения параметра р,
при которых уравнение ![]() (3)
(3)
имеет ровно три решения.
Решении. Уравнение (3) является квадратным относительно р. Перепишем его в виде
![]()
Найдем корни уравнения
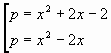
В системе координат (х; р) построим параболы
![]() и
и ![]() (рис.2)
(рис.2)
Данное уравнение имеет три решения при тех значениях параметра р, при которых горизонтальная прямая имеет три точки пересечения с параболами. Таким образом, уравнение (3) имеет три решения в следующих случаях:
1) прямая проходит через вершину одной параболы
и пересекает другую в двух точках. Это возможно,
когда ![]() т.е.
при
т.е.
при ![]() уравнение имеет три решения;
уравнение имеет три решения;
2) прямая проходит через точку пересечения парабол. Найдём абсциссу точки пересечения парабол, для этого решим уравнение
![]()
Если ![]() то
то ![]() т.е. при
т.е. при ![]() прямая
пересекает параболы в трех точках, значит,
исходное уравнение имеет три корня.
прямая
пересекает параболы в трех точках, значит,
исходное уравнение имеет три корня.
Ответ:![]()
![]()
Задача 4. При каких значениях параметра а существует единственная пара (х; у), удовлетворяющая уравнению
![]() (4)
(4)
Решение: Уравнение – квадратное относительно х.
![]() (5)
(5)
1. Контрольным значением параметра является
число ![]() , при
котором уравнение (5) примет вид
, при
котором уравнение (5) примет вид ![]() отсюда
отсюда ![]() . Видно, что в этом случае
решениями уравнения будут все пары
. Видно, что в этом случае
решениями уравнения будут все пары ![]() , т.е. при
, т.е. при ![]() исходное уравнение имеет
бесконечное множество решений.
исходное уравнение имеет
бесконечное множество решений.
2. Пусть ![]() .
Дискриминант уравнения (5)
.
Дискриминант уравнения (5)
![]()
Если ![]() т.е.
т.е. ![]() , то
, то ![]() , исходное
уравнение имеет решение только тогда, когда
, исходное
уравнение имеет решение только тогда, когда ![]() , а
, а ![]() - единственное решение.
- единственное решение.
Если же ![]() ,
исходное уравнение относительно х имеет
решение при любом у.
,
исходное уравнение относительно х имеет
решение при любом у.
Ответ: ![]() .
.
Задача 5. Решите уравнение
![]() (6)
(6)
относительно х
Решение. Уравнение является квадратным относительно р. Перепишем уравнение (6) в виде
![]() (7)
(7)
Дискриминант квадратного уравнения (7)
![]()
Решая (7), получим
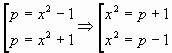
Здесь возможны случаи.
1. Уравнение (6) имеет четыре корня, если
![]()
Решая систему, получаем ![]() . Таким образом, при
. Таким образом, при ![]() уравнение (6) имеет четыре
корня
уравнение (6) имеет четыре
корня ![]() ,
, ![]()
2. Уравнение (6) имеет три корня, если
![]()
Решая систему, получим ![]() Значит, при
Значит, при ![]() уравнение (6) имеет три корня
уравнение (6) имеет три корня ![]()
3. Уравнение (6) имеет два корня, если
![]()
Решая систему, получим ![]() , значит, при этих значениях
параметра р уравнение (6) имеет два корня
, значит, при этих значениях
параметра р уравнение (6) имеет два корня ![]()
4. Уравнение (6) имеет один корень, если
![]()
Решая систему, получим ![]() . Следовательно, при
. Следовательно, при ![]() решением уравнения (6)
будет
решением уравнения (6)
будет ![]() .
.
5. Уравнение (5) не имеет корней, если
![]()
Ответ: если ![]() - корней нет;
- корней нет;
если ![]()
если ![]() ;
;
если ![]()
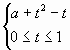
если ![]()
Этот метод не является универсальным, но во многих случаях является весьма результативным и позволяет решать уравнения повышенной сложности. Иногда трудно предвидеть будет ли применение этого метода результативным, но такие уравнения существуют и поэтому его надо знать.
Например, с помощью этого метода можно решить следующие уравнения:
![]() из
сборника для подготовки к ЕГЭ.
из
сборника для подготовки к ЕГЭ.
![]() из
сборника Сканави
из
сборника Сканави
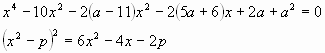
и другие.