Введение (Актуальность темы)
Математика, как и другие науки, изучает действительный мир и, в своих понятиях и законах, отражает закономерности этого мира. Специфика математики как особой науки состоит в том, что она специально выделяет количественные отношения и пространственные формы, которые присущи всем без исключения предметам и явлениям действительности, и делает их объектами своего исследования. Период современной математики обычно относят к середине ХIХ века. К этому времени математика стала настолько абстрактной наукой, что перемахнула за пределы той концепции, которая рассматривала в качестве предмета только число и геометрическую фигуру. Качественные изменения произошли в этот период и в алгебре: значительно расширилось понятие исчисления, различные операции начали производиться не только над числами, но и над векторами, матрицами, логическими высказываниями. В этот период характерно стремление к содержанию единства в многообразии математических фактов и методов, весьма далеких друг от друга. Это выразилось в создании разветвленной теории групп, знаменовавшей собой успехи аксиоматического метода, в дальнейшем развитие теории множеств, общие понятия и методы которой позволили охватить с единой точки зрения области математики, которые ранее казались сильно удаленными друг от друга.
Между математической наукой и математикой учебным предметом существует глубокое внутреннее единство, которое в целом определяется логикой самой науки. Однако это не исключает, а предполагает различие между ними. Наиболее существенное различие между ними заключается, во-первых, в том, что если цель науки – открытие новых закономерностей, то учебная дисциплина преследует педагогические цели обучения и воспитания. Во-вторых, математическая наука способна развиваться неограниченно, в то время как для предмета обучения должны быть указаны “пределы” его предложения в том или ином курсе. И, наконец, если структура науки определяется внутренней логикой ее предмета, то при построении математики как учебного предмета теории и разделы выстраиваются вряд, удобный для лучшего усвоения курса.
Важнейшая задача школы – давать подрастающему поколению глубокие и прочные знания основ наук, вырабатывать навыки и умения, применять их на практике. Одной из основных и главных задач школы является формирование у детей прочных знаний по математике.
Обучение математике должно обеспечить надежную основу, как в отношении знаний и умений учащихся, так и в отношении их развития для дальнейшего изучения математики в 5-11-х классах.
Переход учащихся из начальной школы в среднюю часто сопровождается трудностями адаптации к новым условиям обучения даже в случае, когда начальная и средняя школа работают в рамках единой дидактической темы. Важное значение имеет соотношение между программами по математике в начальной системе и в основном звене. За последние годы произошло значительное обновление содержания математики как в начальной школе, так и в 5-11-х классах. Современное содержание математического образования направлено, главным образом, на интеллектуальное развитие школьников, формирование культуры и самостоятельности их мышления. Существенное усиление алгебраической и геометрической пропедевтики, включение системы содержательно-логических заданий, игр, вопросов направлены на развитие познавательных процессов у детей.
Таким образом, происходящие изменения в структуре и содержании математического образования вызвали ряд проблем, одной из которых является проблема преемственности преподавания математики в школе и ВУЗах и техникумах.
Актуальность данной проблемы заключается в том, что изучение математики невозможно без опоры на знания, полученные в младших классах. Особенно это актуально в связи с вариативным обучением математике. Так, например, учащиеся нашего лицея занимаются по следующим направлениям: гуманитарное, химико-биологическое, знакомятся с элементами комбинаторики, логики, статистики и теории вероятностей.
Исходя из проведенной проблематики и актуальности исследования цель моей работы:
1. Показать влияние решения задач на развитие логического мышления на уроках математики.
Для этого необходимо решить следующие задачи:
1. Разработать и создать сборник задач по математике для развития логического мышления учащихся.
2. Разработать рекомендации для учителей математики по организации обучения математике.
Объектом исследования является процесс обучения математике школьников.
Предметом исследования – решение задач, направленных на развитие логического мышления учащихся.
Глава I. Роль задач в обучении математики.
В связи с развернувшейся в настоящее время во многих странах мира реформой математического образования проблема постановки задач в школьном курсе математики стала одной из самых важных и животрепещущих проблем в развитии преподавания.
Если понятие математической задачи тактируется достаточно широко (в частности, если всякую теорему считать задачей), то решение задач является единственной возможностью для математической деятельности учащихся. Умения решать математические задачи является наиболее яркой характеристикой состояния математического образования.
Как же обстоит дело с обучением учащихся математической деятельности? И, прежде всего, как понимает учащийся (и учитель!) цель постановки задач в школьном курсе математики?
Почти все учащиеся средней школы считают, что если предложенная им математическая задача решена верно, если полученный ответ совпадает с ответом, данным в учебнике, или одобрен учителем, то работа их окончена, о решенной задаче можно и нужно забыть.
Таким образом, учащиеся (а также многие учителя) забывают об обучающем характере каждой задачи, решаемой в процессе обучения, о том, что всякая решаемая ими задача должна учить их умению ориентироваться в различных проблемных ситуациях, обогащать их знания и опыт, учить их математической деятельности.
Проявляя (в традиционной методике обучения решению задач) значительную заботу о применения математических знаний при решении задач и не обращая внимания на процесс актуализации этих знаний, мы нарушаем единство процесса математического мышления и поэтому не можем обеспечить его должного развития у учащихся.
Английский кибернетик Д.М.Маккей установил четыре основные черты, отличающие “интеллект от простой способности вычислять”:
- способность успешно перерабатывать и объединять информацию в зависимости;
- способность совершать пробные действия, поиск и переходы, не вытекающие из наличной информации (т.е. совершать “скачок через разрыв, существующих данных”);
- способность управлять поисковым и исследовательским процессом, руководствуясь “чувством близости решения”;
- способность рассматривать ограниченный, но достаточно большой ряд положений и заключений, совместных с данным положением.
Традиционная система школьных математических задач этим целям пока не отвечает.
Подавляющее большинство задач традиционного школьного курса математики были шаблонными упражнениями тренировочного характера, которые по существу не имеют права на название “задача”.
Но даже эти шаблонные задачи не приведены, как правило, в определенную методическую систему. В этом следует искать ещё одну причину слабого развития способностей к математической деятельности у учащихся средней школы.
К числу недостатков в постановке задач, характерных для традиционного обучения математике, можно отнести, например, следующие:
- излишняя стандартизация содержания и методов решения задач в традиционном обучении;
- увеличение числа решаемых школьниками стандартных задач в ущерб их обучающему качеству;
- излишне узкое понимание роли и целевого назначения математической задачи в процессе обучения;
- несовершенство методики обучения через задачи;
- несоответствие постановки задач и их решений в школе закономерностям развивающего мышления;
- увлечение обучением решению таких задач или таких упражнений, которые в дальнейшем почти не находят приложений ни в процессе изучения основ наук, ни в практике;
- обучение школьников через задачи таким умением и навыком, которые в современной практической деятельности почти не применяются, а в деятельности недалёкого будущего будут переданы автоматическим устройствам;
- отсутствие в школьном курсе математики задач, решение которых могло бы подготовить школьника к деятельности, характерной для современного производства: наладке, управлению, рационализации и т.п.;
- отсутствие чётких критериев учебной значимости каждой задачи, поставленной в процессе обучения, критерия, способного установить необходимое число задач какого-либо типа для достижения реализуемой через них цели обучения, и т.д.
Таким образом, налицо различных аспекты проблемы постановки задач в процессе обучения математике: методический, психологический и даже кибернетический.
Как правило, традиционные школьные математические задачи таковы, что требуют для своего решения определенных знаний, умений или навыков по узкому вопросу программного материала. Поэтому роль и значение их исчерпывается в течение того непродолжительного вопроса программы.
При этом вспомогательная роль таких задач в процессе обучения не является секретарём ни для учащихся, ни для учителя: проиллюстрировать изучаемый теоретический вопрос, разъяснить его смысл, помочь усвоить изучаемый факт через простейшие упражнения, выполняемые по образцу, продиктованному теорией, и только.
Плохо то, что, несмотря на значительные затраты учебного труда и времени на решение таких задач в школе, мы не достигаем ожидаемых результатов для значительного числа выпускников средней школы.
Основным становится формирование у школьника умения ориентироваться в новых задачных ситуациях, накапливать информацию, полезную для решения других задач или изучения новых разделов математики, обучение учащихся разнообразным математическим методам познание реальной действительности и т.д.
Именно этот аспект обучения математике отражён в следующем перечне целей обучения через задачи:
- заинтересовать или мотивировать;
- приводить и практиковать “технику решения задач”;
- формировать понятие математической модели.
Говоря о роли математических задач в развитии у школьников способностей к самостоятельной познавательной деятельности творческого характера, отметим полезность постановки в школьном обучении математических задач проблемного характера.
Правильная постановка задач и упражнений в обучении математике во многом определяет современную методику преподавания, так как решение задач служит различным конкретным целям обучения. Так, например, задачи могут использоваться при введении в изучение новой темы, для самостоятельного установления школьниками какого-либо математического факта, подлежащего изучению или иллюстрации этого факта, с целью глубокого усвоения теоретического материала или выработке необходимых умений и навыков, для контроля знаний и самоконтроля, возбуждения и развития интереса к математике и, наконец, приобщения учащихся к деятельности математического характера– поисковой и творческой, развития у школьников логического математического мышления.
Решение каждой математической задачи осуществляется по четырем основным этапом:
- понимание условия и требования задачи; ясное усвоение и осмысливание отдельных элементов условия;
- составление плана решения;
- практическая реализация плана во всех его деталях;
- окончательное рассмотрение задачи и её решения с целью усвоения тех моментов, которые могут стать полезными для дальнейшего решения задач.
Для выработки правильного понимания школьниками поставленной задачи можно рекомендовать соблюдение следующих требований:
- начинайте изучение условия задачи с аккуратно выполненных схем. Помните, что правильное графическое представление условия задачи означают по существу четкое, ясное и конкретное представление о всей задачной ситуации в целом;
- представьте ясно и детально все основное, связанное с данной задачей. Обстоятельно выясните, что дано, что надо найти; выделите при этом главное в тексте условия задачи и сконцентрируйте на нем своё внимание. Выделите на чертеже данные и искомые величины различными яркими цветами;
- проверьте тщательно каждое выдвигаемое в процессе решения задачи положение контрольными вопросами вида: что это означает, какие имеются основание для данного утверждения, какую пользу можно извлечь из данного факта?
- проверьте, однозначно ли сформулирована задача. Нет ли в условии задачи избыточных или недостающих данных?
Говоря о первой из этих требований, отметим, что оно особенно важно при решении геометрических задач, где наглядный и четкий чертеж позволяет иной раз с первого же взгляда обнаружить возможные пути решения.
Немаловажную роль в успешном решении задач играет целенаправленность поиска решения, т.е. сознательное ограничение числа проб и ошибок, характерных для начальной его стадии.
Иногда учащийся не в состоянии самостоятельно проанализировать задачу и решить ее без помощи учителя. Однако в этом случае не следует сообщать ему готовое решение, а тем более заставлять школьника заучить данный в готовом виде способ действия.
При создании оптимальных условий, которые бы активизировали мыслительную деятельность учащихся при решении задач, весьма часто применяется особый дидактический прием, называемый системой подсказок. Система подсказок, состоящая из вспомогательных задач, вопросов и т.д., не подменяя мышление школьника, придает ему нужное направление, т.е. делает поиск решения целенаправленным.
Полезность упорядочения поисковой деятельности в процессе решения задач школьникам следует продемонстрировать на эффективно подобранной задаче и ее решении.
Например, представьте себе, говорит учитель, что ваш друг задумал некоторое натуральное число в промежутке от 1 до 1024. Чтобы угадать задуманное число, вы будете отвечать на вопросы “да” и “нет”. Может показаться невероятным, но достаточно всего лишь десяти вопросов, чтобы наверняка отгадать любое такое число.
Пусть задуманное число 1.
Спрашиваем:
- Задуманное больше 512 (половину промежутка 1024)? – Нет.
- Оно больше 256? – Нет.
- Оно больше 128 (половину того промежутка, в каком оно может быть)? – Нет.
- Оно больше 64? – Нет.
- Оно больше 32? – Нет.
- Оно больше 16? – Нет.
- Оно больше 8? – Нет.
- Оно больше 4? – Нет.
- Оно больше 2? – Нет.
- Это число 1? – Да.
Итак, постепенно уменьшая область поисков, мы решили задачу. Попробуйте сами решить эту задачу в предположении, что ваш друг задумал число 720; пусть ваш сосед по парте задумает число – угадайте его!
Решение задач требует наличие у школьников так называемых комбинационных способностей, под которыми понимают умение сделать подходящий выбор в условиях избытка активных и пассивных знаний. Понятно, что поиск и отбор полезной для решения данной задачи информации также должен быть целенаправленным. Нередко этот выбор может быть легко осуществлен при обращении к подходящей аналогии.
Отыскание подходящих аналогий активизируется вопросами: “Где мы раньше встречали что – либо подобное, видели что – либо родственное, встречали одинаковые характерные свойства?”
Для простоты отыскания аналогии полезно применять сравнительные чертежи, вспомогательные формулировки.
Применяя аналогию при решении задач, часто бывает полезным изменять формулировку задачи.
Например, пусть в условии некоторой задачи говорится о том, что треугольники АВС делится прямой MN, параллельной основанию на две части (Треугольник и трапецию), площади которых относятся как 2:3.
Еще не начиная решения этой задачи, школьники вспомнят известную им аналогичную по содержанию теорему об отношении площадей подобных треугольников. Но наличие в условии отношения площадей треугольника и трапеции может затормозить стремление использовать эту теорему при решении задачи.
Для этого достаточно сказать, что треугольник АВС делится прямой MN на два треугольника, отношение площадей которых легко установить.
Наконец, аналогия может оказаться полезной на начальном этапе решения задачи. Если уже на этом этапе удается сравнить данную задачу с задачами, решенными ранее, то сходство условий, требований, способа решения и т.д., часто сразу “наталкивает” учащихся на плодотворные идеи при планировании решения.
Очевидно, что решение многих математических задач сводится к решению некоторых частных задач, а последние, в свою очередь, расчленяются на простые задачи, решение которых или постулируется (например, в задачах на построение), или же находится из определений и аксиом.
Учителю необходимо научить ребят видеть составные задачи в ходе решения основной, научить составлять их, так как только благодаря такой работе возможен успешный поиск решения задач.
До недавнего времени в школьном обучении математике мало уделялось внимания такому важному виду математической деятельности учащихся, каким является самостоятельное составление тех или иных математических задач. Умение школьников составлять свои задачи по заранее известным условиям, по аналогии с данной задачей и т.д. является весьма ценным.
Например, дано уравнение: 8х – 3 = 5х +6. Составить задачу, решение которой приводит к решению этого уравнения.
Показ учителем способа составления некоторой задачи превращает аналогичное задание не только в доступное для всех, но даже – в стандартное. Помощь учителя должна быть и в этом случае дидактически разумной.
Рассмотрим пример того, как решение готового уравнения сопровождается самостоятельным составлением аналогичных уравнений:

Такая форма “параллельных” записей облегчает учебную деятельность школьников по составлению задач.
Значительно оживляют уроки математики и дидактические весьма полезны различные занимательные задачи, нешаблонные вопросы и “задачи на смекалку”.
Задачи – шутки и вопросы на сообразительность (для устного решения).
- На дереве сидело 10 птиц. Охотник выстрелил и подстрелил одну птицу. Сколько птиц осталось на дереве?
- Как из трех спичек, не ломая их, образовать четыре?
В такого рода задачах необходимо увидеть и преодолеть психологический барьер.
Задачи типа “Внимателен ли ты?” Такие вопросы и задачи развивают внимание и наблюдательность школьников.
- Сколько углов на чертеже?
- Сколько кубиков на чертеже?
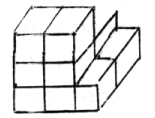
Очень интересными, своеобразными задачами являются так называемые дудлы, которые обычно вызывают у ребят большое желание самим придумывать и задавать их друг другу.
Что это такое?
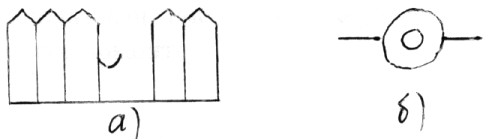
Возможны ответы: на рисунке а – проходящий вдоль забора солдат с собакой; на рисунке б – человек в сомбреро, едущий на велосипеде, т.д.
Полезными и нужными являются задачи на отыскание всевозможных закономерностей. Такие задачи формируют навыки математического мышления: умение анализировать, обобщать, находить закономерности.
Какое слово надо выкинуть как “из ряда вон выходящее”: кортик, падеж, стакан, книга, паркет?
Учителю полезно использовать подобного рода задачи не только на внеклассных занятиях по математике, но и на обычных уроках.
Чем же должен руководствоваться учитель при подборе учебных задач?
Рассмотрим памятку для анализа педагогической ценности задачи:
- Какую учебную цель преследует данная задача?
- Какие элементы математического образования имеются в виду?
- Необходима ли именно эта задача?
- Почему такие, а не другие.
- Почему выбрана такая фабула задачи?
- Почему взяты такие, а не другие числовые данные?
- Отвечают ли числовые данные реальной обстановке, в которой могла бы возникнуть аналогичная задача?
- Интересна ли задача для учащихся, увлекательна, естественная ли постановка вопроса, вызывает ли она у учащихся интерес к ответу или способу решения, чем именно?
- Сможет ли учащийся самостоятельно решить данную задачу? Что он для этого должен знать, уметь, помнить, представлять себе? Если учащийся не сможет этого сделать, о чем будет свидетельствовать этот факт?
- Чем и в какой мере ему может и должен помочь учитель?
- Как эта задача связана с предшествующий и последующей учебной работой учащегося? И т.д.
Давая такую оценку каждой учебной задаче, учитель сумеет при минимальной затрате учебного времени добиться хороших результатов как в обучении, так и в развитии математического мышления школьников.
Но учиться не только должен сам уметь оценивать задачу, выявляя все ее полезные учебные качества, он должен научиться этому и учащихся.
Даже очень хорошие учащиеся, получив ответ на вопрос задачи и тщательно изложив ход ее решения, закрывают тетрадь, пологая работу законченной. Учитель обязан понимать, что никакую задачу нельзя исчерпать до конца. Этот взгляд он должен прививать и своим ученикам. всегда остается что – нибудь, над чем можно и нужно поразмышлять; всегда можно усовершенствовать любое решение, глубже его осмыслить, выявить полезную и новую для учащихся информацию. Поэтому после решения каждой задачи следует еще раз оглянуться назад, обратить внимание на метод, который был использован, попытаться найти другие пути решения, выявить то, что необходимо помнить.
Решение одной задачи несколькими способами часто бывает более полезным, чем решение одним способом нескольких задач, так как при оценке способов решения задачи активно работают такие умственные операции, как анализ, сравнения, обобщения и другие. А это, несомненно, оказывает свое положительное влияние на развитие математического мышления школьников.
Прежде чем говорить о том, какие математические задачи следует рассматривать в школьном курсе математики и как обучать школьников решению задач, нужно уточнить, что следует понимать под термином “задача”.
Например, уравнение 11423*х = 616842 представляет проблемную ситуацию для любого человека. Но проблемную ситуацию является понятием относительным. Например, ситуация, выраженная уравнением х+9=10, является проблемной для начинающего школьника и не является таковой для учащихся старших классов.
Числовое равенство 123+2*х=197 становится задачей, если оно сопровождается целевым заданием “решить уравнение”.
Решить задачу – значит преобразовать данную проблемную ситуацию или установить, что такое преобразование в данных условиях (или в данной среде) невозможно.
Естественно определить процесс решения задачи как целенаправленную мыслительную или практическую деятельность человека, осуществляющего решение задачи.
Глава II. Формирование интеллектуальных умений
Создание учебных проблемных ситуаций на уроке математики – оправдавшей себя на практике дидактический прием, посредством которого учитель держит в постоянном напряжении одну из внутренних пружин процесса обучения – детская любознательность.
Справедливо указывает академик АН УССР Б.В.Чиденко: “Потеря интереса к обучению, на каком – то этапе рождает безразличие и апатию, безразличие рождает лень, а лень – безделье и потерю способностей. Вот почему важно продумать курс математики так, чтобы его изучение было интересно; содержание было совершенно, будило мысль и развивало способности, а также открывало пути, как в научную, так и в практическую деятельность”.
Учебные проблемы, которые ставятся перед учеником, могут решаться на протяжении как одного, так и нескольких уроков; они могут выступать и форме обычных вопросов к учащимся, таких, например, как:
- Почему треугольник назван треугольником? Можно ли дать ему другое название, также связанное с его свойствами?
- Как можно объяснить название “развернутый угол”?
- Как бы вы назвали треугольник, у которого один угол прямой? (Вопрос задается до ознакомления с этим термином.)
Учебную проблемную ситуацию можно создать при решении любой задачи. Рассмотрим одну из задач: решить квадратное уравнение: х2 –5х+6=0.
Что известно о решении квадратного уравнения? О его свойствах?
а) х1 х2=-p/2 ![]()
б) теорема Виета: х + х = – р; х * х = q;
в) если х – корень уравнения, то х21 + 5х2 + 6 =0 – верное равенство.
Необходимо подвести учащихся к тому, чтобы они сами поставили перед собой вопросы: что можно извлечь из этих знаний? Что можно и интересно было бы узнать? Какие задачи можно составить, отправлять от этого уравнения? Например:
- Пусть х1 и х2 – корни уравнения; нельзя ли иначе, чем в учебнике получить теорему Виета?
- Нельзя ли распространить теорему Виета на уравнения х3+рх2+qх+е=0? (Проблема!)
- Как можно еще решить квадратное уравнение? (Не зная формулы его решения.)
- Нельзя ли решение уравнения х3+рх2+qх+е=0 свести к решению системы трех уравнений с тремя неизвестными? (Проблема!)
- Какими интересными свойствами обладает квадратный трехчлен f(х)=х2–5х+6?
- Как установить, при каких значениях х f(х)=х2–5х+6 имеет наименьшее значение?
- Нельзя ли решить геометрически квадратное уравнение х2 –5х+6 = 0?
Проблемные ситуации в обучении математике возникают также в случае необходимости проверить умозаключение, сделанное на основе интуиции, на основе аналогии или попытке общения. Примеры таких проблем:
- Между углами и сторонами треугольника имеются определенные зависимости. Сохраняются ли они для четырехугольника?
- Средняя линяя треугольника параллельна основаниям. А у ромба? У параллелограмма? У любого четырехугольника?
- Равнобедренный треугольник имеет определенные свойства. А равнобедренная трапеция? Сохраняются ли для нее аналогичные свойства?
Очень часто проблемность достигает выполнением какого-то практического упражнения или решением соответствующей задачи. Например: Какие углы может иметь равнобедренная трапеция, если она разбивается диагонально на два равнобедренных треугольника?
Проблемность этой задачи заключается в умении увидеть все случаи, исчерпать все возможное в этой задаче.
1.Ответ:углы ВАД=СДА=720, углыАВС=ДСВ=1080
2.Ответ:углы А=В=С=Д=900(частный случай трапеции)
3.Ответ:углы А=С=1200, В=Д=600 и т.д.
Интересными задачами-проблемами являются задачи, ведущие к открытию новой теории.
Своеобразие нестандартных задач заключается в том, что почти каждая из них – это маленькая проблема. Решение маленьких математических проблем опирается не столько на специальные знание, сколько на сообразительность и изобретательность. Эти качества ума и необходимо активно развивать у школьников.
В процессе решения учебных математических задач следует уделять особое внимание актуализации знаний учащихся. С этой точки зрения весьма полезны специально подобранные серии задач, составленные так, чтобы научить школьников умело пользоваться прошлым опытом при поиске решения новой задачи.
Прежде чем предложить трудную нестандартную задачу, учащимся было предложена довольно простоя задача:
1.Дан прямоугольный треугольник со сторонами 3см. и 4см. Найти длину медианы, проведенной к гипотенузе.
Школьники предложили два способа решения:
1 – й способ. | АВ | = ![]() =5 (см).
Достроим прямоугольный треугольник до
прямоугольника. А в прямоугольнике диагонали
конгруэнтны и в точке переcеxxeия делятся пополам:
| СМ | = 2,5 см.
=5 (см).
Достроим прямоугольный треугольник до
прямоугольника. А в прямоугольнике диагонали
конгруэнтны и в точке переcеxxeия делятся пополам:
| СМ | = 2,5 см.
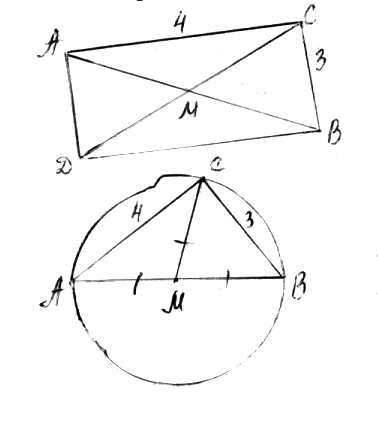
2– й способ. | АВ | =5 см – египетских треугольник. Точка М является центром описанной окружности, тогда | СМ | = 1/2*|АВ| = 2,5, так как СМ – радиус этой окружности, а АВ – ее диаметр.
Вместе со школьниками учитель сравнивает оба способа решения. Установили, что по сложности они равноценны, но второй способ более интересен, так как он необычен: надо уметь пользоваться свойствами описанной окружности.
Учитель ставит вопрос: как обобщить задачу, ведь в этой конкретные данные? Школьники сами сформулировали условие более общей задачи.
2.Доказать, что медиана, проведенная из вершины прямого угла треугольника, равна половине гипотенузы.
Тем самым было установлено свойство медианы прямоугольного треугольника, проведенной из вершины прямого угла на гипотенузу. (Этим определяется учебная полезность задачи – расширения теоретической базы).
Затем учитель предложил следующую задачу:
3.Доказать, что в прямоугольном треугольнике биссектриса прямого угла делит пополам угол между медианой и высотой, проведенными к гипотенузе.
Школьники справились с задачей самостоятельно и почти у каждого – свой способ решения.
Учащиеся сравнили все эти способы и подвели итог:
- нужно смелее пользоваться дополнительными построениями;
- активнее применять соответствующие разделы теории;
- полезно с разных сторон “подходить” к рисунку – чертенку, находить в нем важную особенность и суметь воспользоваться ею.
Была составлена и обратная задача: если медиана и высота, проведенная из одной вершины треугольника, делят величину его угла на три равные части, то этот треугольник прямоугольный.
Эту задачу школьники решили также разными способами. Далее учитель провел обобщение, указав на взаимосвязь высоты, медианы и биссектрисы в прямоугольном треугольнике. В равнобедренном прямоугольном треугольнике высота, биссектриса и медиана совпадают.
При движении точки С окружности высота и биссектриса “отходят” от медианы. Биссектриса делит угол между ними пополам. Когда угол В=600– второй частный случай, обладающей тем свойством, что углы, образованные катетами, медианой и высотой, конгруэнтны. При дальнейшем перемещении точки С угол между медианой и высотой увеличиваются, а свойство биссектрисы остается.
В процессе решения этих задач учащиеся использовали для связи элементов треугольника описанную окружность.
Эта серия задач оказалась весьма полезной для учащихся, так как она способствовала развитию у них умения нешаблонно, с интересом подойти к решению задач, побудило их к составлению новых задач, систематизировала известные знания и опыт, т.е. содействовала всестороннему развитию их математического мышления.
При решении этих задач у учащихся развивалась способность и потребность к актуализации (упорядочению знай и опыта и умению применить его в новой ситуации). Тем самым мне удалось в какой – то мере реализовать то, что следует называть обучением решению задач.
2.1. Рекомендации по организации обучения математики
Сравнительный анализ результатов выполнения базовых заданий одинаковой тематики в 2002—2005 гг. по алгебре и началам анализа показывает, что из года в год повторяются типичные ошибки. Авторам учебников и разработчикам методических пособий следует обратить внимание на формирование базовых умений. Очевидны и проблемы, связанные с организацией обучения математике в средней школе. Одна из основных проблем состоит в том, что из года в год значительный процент выпускников не овладевает даже минимумом содержания, предусмотренным программой по математике: школьники делают ошибки при прямом применении изучаемых фактов и свойств, стандартных методов решения уравнений и неравенств, на распознавание и применение свойств функций. Так, например:
при делении степеней с одинаковыми основаниями “теряется” основание степени;
— в качестве правильного школьники выбирают тот ответ, где разность логарифмов представлена как логарифм разности;
— при решении иррациональных уравнений большинство
выпускников правильно находят корни уравнения-следствия, но не выясняют, какие из них являются корнями исходного уравнения;
— при решении логарифмических неравенств выпускники часто не учитывают область определения логарифмической функций, не меняют знак неравенства при переходе к линейному неравенству в том случае, когда основание логарифма меньше 1; не представляют число, стоящее в правой части неравенства, как значение логарифма;
— путают понятия “множество значений” и “область определения” функции при описании её свойств.
Подобные ошибки свидетельствуют о том, что в процессе обучения не было уделено должного внимания отработке базовых умений. В этой связи учителя справедливо отмечают, что в базисном учебном плане старшей школы отводится недостаточно времени на математику: это, по их мнению, приводит к тому, что многим ученикам не хватает учебного времени на прочное усвоение изучаемых тем.
В педагогической и методической литературе много говорится об индивидуализации обучения, об учёте готовности ученика к восприятию материала, о дозировании заданий с, учётом потребностей и возможностей школьника, но традиционно урок готовится в расчёте на некоего усреднённого. Ученика, что и приводит к столь невысоким результатам обучения. Поэтому и возникают сомнения в том, что могут быть рекомендации, пригодные для всех. Ведь каждый ученик личность, и в каждом классе есть ребята, которые схватывают всё на лету, и такие, которым всё надо подробнейшим образом несколько раз пояснить; увлечённые математикой и не любящие её; готовые много заниматься математикой дома и не притрагивающиеся к учебнику.
И тем не менее, несмотря на все индивидуальные отличия школьников, существует нечто в организации учебного процесса по математике при классноурочной системе обучения, определяющее успешность или неуспешность усвоения материала: объективные закономерности усвоения. Ясно, что понимание этих закономерностей и следование им в реальном педагогическом процессе – важнейший резерв повышения эффективности обучения только формулировки теорем и следствий и них и вовсе не рассматриваются их обоснования; при этом, как правило, не систематизируются имеющиеся и не обобщаются новые и ранее полученные знания. Даже при систематизации материала не всегда расставляются акценты – какой учебный материал важнее для решения конкретных задач по теме (а значит, и приоритеты в изучении). Действительно, в каждом из рассмотренных случаев не обеспечивается прочное усвоение большинством учеников класса ни программного, ни дополнительного материала, поскольку мы изначально недостаточно чётко определили цель изучения того или иного материала, а, следовательно, некачественно организовали деятельность всех учеников класса.
Следствием этого становится несформированность у старшеклассников умения самостоятельно добиваться знания и использовать их в несколько изменённой ситуации.
Как известно, наиболее трудна и для слабых, и для сильных школьников
“Тригонометрия”: слишком много формул и недостаточно времени на их отработку. В варианты КИМ был включён справочный материал, в котором содержались формулы по тригонометрии (косинус(синус)суммы (разности), из которых самыми элементарными способами получались следствия (формулы приведения, двойного угла). Результаты выполнения заданий на применение формул приведения и нахождение синуса (косинуса) двойного угла позволяют сделать вывод о том, что для многих учащихся справочный материал бесполезен, поскольку они не умеют им пользоваться.
Итак, правильный отбор изучаемого материала, ориентированный на минимум содержания и требования стандарта, создаст предпосылки для продуктивного изучения, но не обеспечит его без следования основам теории поэтапного формирования умственных действий.
Л.С Выгодский утверждал, что знания усваиваются только в процессе собственной работы обучаемого с этими знаниями. Из чего можно сделать важный практический вывод: главная задача преподавателя на уроке — организовать собственную самостоятельную работу каждого ученика с материалом, который нужно усвоить.
Если учитель это понимает, он сведёт свои пояснения и разъяснения к “оптимальному минимуму”, посвятив всё остальное время урока управлению той работой, которую выполняет на уроке с изучаемым материалом каждый из учеников. Очевидно, что чем меньше учитель говорит сам, чем больше он направляет и контролирует работу каждого из учеников класса, тем эффективнее обучение.
В соответствии с этой теорией преподаватель должен не только объяснить новый материал так, чтобы каждый ученик понял, что же именно ему надо усвоить и как работать с этим материалом, но и фиксировать основное содержание материала, которое позволяет приступить к работе без всякого предварительного заучивания.
Рассмотрим вторую проблему преподавания: закрепление базовых умений на уроках математики.
Объясняя материал и кратко его записывая на этапе ориентировки, учитель должен расчленить его на отдельные порции. Работа с каждой порцией — самостоятельный шаг ученика, отдельная операция. Необходимо организовать первоначальное закрепление материала так, чтобы учитель имел возможность проконтролировать ход и результаты выполнения каждой операции. Именно поэтому нельзя допустить, чтобы на этом этапе работа велась в уме. Итак, схема организации усвоения нового материала, в соответствии с теорией поэтапного формирования умственных действий, имеет следующий вид:
-фиксирование основного содержания подлежащего усвоению материала и способов работы с ним в краткой схематичной форме, удобной для использования при решении задач;
-организация самостоятельной работы, позволяющей проконтролировать ход работы и её результаты;
-постепенный переход от пошагового контроля со стороны преподавателя к самоконтролю обучающихся.
Может показаться, что при столь серьёзной и продолжительной организации процесса объяснения и первоначального закрепления с учётом малого количества часов, отводимого на изучение математики базисным учебным планом старшей школы, не хватит времени на закрепление с применением варьирования: при знакомстве с новыми объектами придётся ограничиться лишь стандартными ситуациями, что, с одной стороны, несомненно, приведёт к ошибкам, а с другой стороны, будет препятствовать развитию сильных учащихся. Однако по результатам многолетних экспериментов, проведённых в школах под руководством Н.Ф. Талызиной, сделан вывод о том, что если учить плохо; если в результате обучения определение не становится для ученика руководством к действию; если, выполняя распознавание, ученик (сильный или слабый) руководствуется сложившимся в сознании эталоном, и только им; если его не научили опираться при распознавании на определение, то варьирование несущественных признаков единственное, что может помочь сформировать обобщённый, освобождённый от случайных, несущественных свойств зрительный образ. А если та кой образ не сформирован неоткуда взяться правильному решению.
Но если учить хорошо, если обеспечить подлинное усвоение определения — значение варьирования оказывается неизмеримо более скромным.
Открытость требований к проведению ЕГЭ, возможность познакомиться с планом экзаменационной работы на текущий учебный год и демонстрационным вариантом, поучаствовать в пробном экзамене по этому предмету важные, но недостаточные условия успеха. Умение анализировать ситуацию и делать выводы на основании имеющихся теоретических знаний безусловно, одна из самых важных составляющих успеха на экзамене по математике. Достаточно популярно такое закрепление, как решение множества однотипных упражнении для того, чтобы “набить руку”. Выделил и “новый” приём работы в выпускных классах в конце учебного года — постепенное (в некоторых школах, еженедельное) выполнение работ, составленных по типу ЕГЭ. Большинство учителей не имеют и тени сомнения в том, что выполнение множества однотипных заданий совершенно необходимое условие успешного усвоения и залог успеха. Правда, они же вынуждены констатировать, что однотипные задачи сильным ученикам скучны и неинтересны.
Изучив итоги пятилетней работы по введению Единого Государственного Экзамена по математике, можно утверждать: механизм проведения итоговой аттестации в форме ЕГЭ позволяет констатировать, что значительная часть выпускников российских школ выполняет большинство требований стандарта. Вместе с тем очевидны серьезные пробелы в работе педагогов с теми школьниками, которые не овладевают этими требованиями.
Среди нереализованных педагогами возможностей повышения качества математического образования главная — совершенствование подготовки и проведения урока математики на основе:
– более активного внедрения в практику работы школы принципов индивидуализации и дифференциации обучения;
использования активных форм организации деятельности школьников (а не собственной деятельности педагога);
– организации самостоятельной работы учащихся по усвоению изучаемого материала;
– внедрения проверенных и признанных на практике достижений в области педагогической психологии.
Итоговая аттестация в форме ЕГЭ не требует от педагогов изменения методики преподавания математики, а потому проблемы, возникающие в подготовке как слабых так и сильных учеников можно рассматривать как следствие недостаточной реализации потенциала современного урока.
Один из потенциалов – это использование информационных технологий на уроках математики. Оно делает обучение более содержательным, зрелищным, способствует развитию самостоятельности и творческих способностей обучаемого, существенно повышает уровень индивидуализации обучения. Ученикам, обладающим высокими учебными возможностями, они создают условия за то же самое время получить углубленные или расширенные знания, что значительно экономит время ребенка и учителя. Причем ребенок сам выбирает и уровень учебного материала, который может усвоить. Полностью решается проблема пропущенного материала. Необходимо также отметить интерес ребенка к использованию компьютера на уроках математики.
Для проверки усвоения знаний учащихся можно использовать компьютерные тесты. Особенность их в том, что ученик в случае ошибки может видеть образец правильного ответа. Компьютерные тесты хорошо использовать не только для контроля знаний, но и для самоконтроля, как при подготовке к контрольным работам, так и для повторения ранее изученного материала, знание которого потребуется при изучении новой темы. Учащимися старших классов можно использовать эти тесты для повторения материала перед экзаменом. Особенно примечательным является тот факт, что те ученики, которые психологически не справляются на письменных контрольных работах, очень успешны при сдаче и выполнении работ с помощью тестов.
Важную роль играют при изучении математики уроки-презентации. На таких уроках реализуются принципы доступности, наглядности. Уроки эффетивны своей эстетической привлекательностью, также между учителем и учеником существует посредник — компьютер, что способствует часто эффективному взаимодействию. Урок-презентация также обеспечивает большой объем информации и заданий за короткий период. Всегда можно вернуться к предыдущему слайду.
Важным положительным эффектом применения компьютерной техники на уроке является повышение мотивации учения. При этом особенно ярко видно влияние новых компьютерных средств преподавания на “слабых” учащихся; для многих из них работа с компьютером оказывается той единственной ступенькой к возрождению интереса к учебе, возможностью добиться успеха. Учащиеся охотно создают презентации, используя дополнительный материал, возможности Интернета, собственные знания по информатике и математике.
Применение информационных технологий при изучении различных предметов в первую очередь требует высокой подготовки учителя, который знаком с этими программами и умеет с ними работать. Во-вторых, уроки с применением компьютера позволяют выполнить больший объем заданий, операций, действий и при этом качественно. Возможности программного обеспечения растут с каждым днем, компьютер все больше и больше внедряется во все сферы общества. Поэтому каждому учителю необходимо научиться использовать информационные технологии в образовании.
Заключение
Урок был и остается основной формой организации учебно-воспитательного процесса. Сущность урока составляет организация учителем разнообразной работы учащихся по усвоению новых знаний, умений, навыков, в ходе которой осуществляется их воспитание и развитие. Современный урок-это урок, на котором учитель умело использует все возможные формы организации познавательной деятельности учащихся.
При решении задач у учащихся развивалась способность и потребность к актуализации (упорядочению знаний и опыты и умению применять его в новой ситуации). В работе даны основные подходы к решению творческих задач, требующих использования логических способностей. Предложена целенаправленная подборка развивающих задач на применение элементарных и сложных логических операций, связанных с поиском закономерностей, связей, отношений, причин, следствий. Выполнение предложенных заданий является еще одним переходным шагом к развитию логического, комбинационного, версионного, метафорического мышления как основных характеристик творческих способностей.
Тем самым мне удалось в какой-то мере реализовать то, что следует называть обучением решению задач и, разработать рекомендации для учителей математики по организации обучения математики.
Литература
Приложение
1. На трех жестяных банках с печеньем перепутаны этикетки “Овсяное печенье”, “Шоколадное печенье” и “Миндальное печенье”. Все этикетки расположены неправильно. Банки закрыты, внутрь заглянуть нельзя. Вы можете открыть только одну банку, после чего правильно расположить этикетки.
2. Маше 16 лет и она на 5 см выше Эрика. Дима, Машин брат, ростом ниже Маши. Эрик – единственный ребенок в семье”. Какое из следующих утверждений наиболее точно?
1. Дима выше Эрика. 2. Дима ниже Эрика. 3. Дима такого же роста, как Эрик; 4. Нельзя точно сказать, кто выше – Дима или Эрик. Зачем здесь возраст?
3. Бегуны прошли дистанцию и на табло загорелась надпись: Рустам не был вторым Эдуард отстал от Рустама на 2 места Яков не был первым Галина не была ни первой, ни последней Карина финишировала сразу после Якова Каково распределение бегунов на финише?
Подзадача 1: Кто был первым?
4. Фрэнк Стокман. Принцесса или тигр ? (сказка)
Узник должен угадать, в какой из двух комнат находится принцесса, а в какой тигр. Если он угадает комнату принцессы, то женится на ней, если ошибется, его растерзает тигр.
В первый день были проведены три испытания, При этом король объявил узнику, что в ходе всех грех испытаний в какой – то из комнат будет находиться либо принцесса, либо игр, причем может оказаться, что в какой комнате будет по тигру или там окажутся одни принцессы.
На комнатах висят таблички. На первой: “В этой комнате находится принцесса, а в другой сидит тигр”. На второй:
В одной из комнат находится принцесса, кроме того, в одной из этих комнат сидит тигр.
В какой комнате находится принцесса, если на одной табличке написана правда, на другой – ложь?
5. Из двух братьев-близнецов один всегда лжет, другой всегда говорит правду. Как можно узнать, кто из них лжец, задав только один вопрос?
6. Одного из этих близнецов зовут Джон. Как узнать, которого, если можно задать ему только 1 вопрос из 3-х слов?
7. Борис выше Маши, которая, в свою очередь, выше Степы. Рома, Машин брат, такого же роста, как и Дима, который на З см ниже Бориса. Какое из следующих утверждений является верным?
а) Борис и Степа одного роста.
б) Дима и Рома – братья.
в) Борис – второй по росту в этой компании.
г) Ни одно из этих утверждений не является правильным.
(Правильный ответ – “г”)
8. Логическое рассуждение: Если З дня назад был день, предшествующий понедельнику, то какой день будет послезавтра?
9. Утомившись от споров и летнего зноя, 3 греческих мудреца уснули под деревом. Пока они спали, шутники испачкали углем их лбы. Проснувшись и взглянув друг на друга, все 3 пришли в веселое настроение и начали смеяться. Но это никого не тревожило, так как каждому казалось естественным, что двое других смеются друг над другом.
Внезапно один из мудрецов перестал смеяться , так как сообразил, что его лоб также испачкан. С чего эго он взял?
10. Вот тебе сковорода, – сказал Король. – Испечешь мне наконец кренделей или нет?
– Без рецепта? – спросила Королева.
– Воспользуйся своим обычным рецептом, – закричал нетерпеливо Король. – В прошлый раз крендели у тебя удались на славу!
– Не могу, – ответила Королева. – В прошлый раз я испекла крендели по рецепту из моей поваренной книги, а её-то и украли!
Наибольшие подозрения пали на кухарку Герцогини. Поваренную книгу действительно нашли на кухне у Герцогини. Похитить её могли только кухарка, Герцогиня и Чеширский Кот.
– Поваренную книгу украл Чеширский Кот! – сказала Герцогиня на суде.
– О да, поваренную книгу украл я! – согласился Чеширский Кот.
– Я не крала поваренную книгу! – утверждала кухарка. Выяснилось, что лгал тот, кто украл поваренную книгу, и что по крайней мере один из остальных говорил правду.
Кто украл поваренную книгу?
11. После того, как поваренную книгу была возвращена Королеве, её украли во второй раз. И опять подозрение пало на Герцогилю, кухарку и Чеширского Кота. На суде все трое дали те же показания, что и в прошлый раз. Но теперь тот, кто похитил поваренную книгу, солгал, а двое других сказали правду.
Кто украл поваренную книгу на этот раз?
12. – Вот тебе твоя поваренная книга, – сказал Ко-
– Теперь и рецепт у тебя есть. Испеки мне кренделей!
– Без молока, без масла, без яиц?
– Горе мне! – вскричал Король. – Это уж слишком!
– Но теперь я точно знаю, кто украл мои припасы! Это сделали Мартовский Заяц, Болванщик и Соня, – закричала Королева, топая ногами от ярости.
Когда я вошла в кухню, то видела, как они вылезали из окна. И каждый нес с собой что-нибудь из припасов, только я не разглядела, что у кого было.
– Это мы скоро выясним, – грозно пообещал Король. Все припасы были найдены в домике, где жили Мартовский Заяц, Болванщик и Соня. Все трое были взяты под стражу и дали на суде следующие показания:
Мартовский Заяц. Масло украл Болванщик.
Болванщик. Яйца украла Соня.
Соня. Я украла молоко.
В ходе судебного разбирательства выяснилось, что тот, кто украл масло, говорил правду, а тот, кто украл яйца, лгал.
Кто что украл?