По определению, выражения, содержащие знак корня (радикал), называются иррациональными.
При нахождении численных значений корней выражений результатом вычислений могут быть действительные и комплексные числа. В свою очередь, действительные числа могут быть как рациональные, так и иррациональные.
Напомним, что рациональное число является обыкновенной дробью, которую, в свою очередь, можно представить в виде десятичной конечной или десятичной периодической дроби, иррациональное же число можно представить только в виде десятичной бесконечной непериодической дроби.
Внесем некоторые уточнения в понятия “иррациональные выражение, число”. Так, например, корни квадратного уравнения с действительными коэффициентами ![]() являются иррациональными выражениями:
являются иррациональными выражениями:
![]() . Этим же термином – иррациональные выражения называются также и
. Этим же термином – иррациональные выражения называются также и ![]() . То есть, различия в терминологии иррациональности применительно к выражениям
. То есть, различия в терминологии иррациональности применительно к выражениям ![]() и
и ![]() нет, хотя первое из них, кроме собственно иррациональности, содержит также рациональное слагаемое
нет, хотя первое из них, кроме собственно иррациональности, содержит также рациональное слагаемое ![]() . Так же, например, иррациональными числами являются
. Так же, например, иррациональными числами являются ![]() и корни
и корни ![]() квадратного уравнения
квадратного уравнения ![]() . Различия в терминологии для обозначения чисел
. Различия в терминологии для обозначения чисел ![]() и
и ![]() тоже нет.
тоже нет.
В существующей в настоящее время математической терминологии выражения вида ![]() и
и ![]() , где
, где ![]() − рациональное выражение, именуются одинаково – иррациональные. Это же относится и к иррациональным числам.
− рациональное выражение, именуются одинаково – иррациональные. Это же относится и к иррациональным числам.
С целью различать иррациональные выражения, числа вида ![]() и
и ![]() введем термин (понятие) ”чисто иррациональное выражение, число ”.
введем термин (понятие) ”чисто иррациональное выражение, число ”.
Чисто иррациональным выражением, числом назовем корень n-й степени из действительного алгебраического выражения, числа без рациональных составляющих в виде слагаемых.
Таким образом, в приведенных выше примерах, чисто иррациональными будут являться выражения ![]() ,
, ![]() и числа
и числа ![]() .
.
Необходимость введения здесь понятий “чисто иррациональное выражение, число” несколько аналогична необходимости введения в математике понятия “чисто мнимое число” с целью отличия его от “мнимого числа (комплексного числа)”.
Остановимся далее на рассмотрении некоторых свойств алгебраических сумм действительных значений двух чисто иррациональных выражений
Пусть имеется алгебраическая сумма двух некоторых действительных чисто иррациональных выражений ![]() , где
, где ![]() − рациональное выражение (число).
− рациональное выражение (число).
Рассмотрим следующие варианты:
1) результатом вычисления каждого в отдельности выражений ![]() и
и ![]() являются рациональные числа. В этом случае их алгебраическая сумма
являются рациональные числа. В этом случае их алгебраическая сумма ![]() будет также рациональной;
будет также рациональной;
2) результатом вычисления одного из выражений ![]() или
или ![]() является рациональное число, вычисления другого – иррациональное. Очевидно, что в этом случае их алгебраическая сумма
является рациональное число, вычисления другого – иррациональное. Очевидно, что в этом случае их алгебраическая сумма ![]() не может быть только рациональной;
не может быть только рациональной;
3) в результате вычисления каждого в отдельности чисто иррационального выражения ![]() и
и ![]() получаем иррациональные числа. Может ли в этом случае сумма (разность) двух чисто иррациональных выражений быть равной рациональному выражению? При решении определенных задач постановка такого вопроса вполне возможна, отсюда следует и необходимость ответа на него. Поэтому остановимся на рассмотрении 3-го из данных случаев. То есть здесь будем рассматривать только случай, когда численными значениями корней являются действительные иррациональные числа. Начнем со следующего примера:
получаем иррациональные числа. Может ли в этом случае сумма (разность) двух чисто иррациональных выражений быть равной рациональному выражению? При решении определенных задач постановка такого вопроса вполне возможна, отсюда следует и необходимость ответа на него. Поэтому остановимся на рассмотрении 3-го из данных случаев. То есть здесь будем рассматривать только случай, когда численными значениями корней являются действительные иррациональные числа. Начнем со следующего примера:
Пример 1.
Пусть имеются два чисто иррациональных выражения ![]() (1) и
(1) и  (2), где
(2), где ![]() − действительное число,
− действительное число, ![]() и
и ![]() − рациональное,
− рациональное, ![]() , для которых выполняются условия
, для которых выполняются условия ![]() и
и  , поскольку рассматриваем только действительные значения чисто иррациональных выражений. По условию, значения
, поскольку рассматриваем только действительные значения чисто иррациональных выражений. По условию, значения ![]() и
и ![]() такие, что в результате вычисления каждого в отдельности выражений (1) и (2) получаем иррациональные числа.
такие, что в результате вычисления каждого в отдельности выражений (1) и (2) получаем иррациональные числа.
Попытаемся определить признаки, при которых алгебраическая сумма двух действительных чисто иррациональных выражений может равняться рациональному выражению.
Вернемся к выражениям (1) и (2), их алгебраическая сумма равна рациональному выражению ![]() , то есть, имеем в данном случае верное равенство
, то есть, имеем в данном случае верное равенство
![]()
 (3).
(3).
Покажем справедливость записанного равенства:
![]()

![]()
![]()
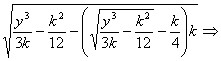
![]()
![]()
![]()
![]() .
.
Отметим очевидный внешний признак – выражение (1) входит в состав выражения (2). Выражение, которое включает в свой состав другое выражение рассматриваемой алгебраической суммы, назовем сложным выражением. Так, здесь выражение (2) будет сложным выражением.
Если ни одно из выражений алгебраической суммы двух чисто иррациональных выражений не включает в свой состав другого, назовем такие чисто иррациональные выражения взаимно простыми выражениями.
Как видим из рассмотренного примера, разность двух чисто иррациональных выражений может равняться рациональному выражению, причем одно из выражений разности входит в состав другого, то есть в данном случае второе выражение является сложным.
Попытаемся определить общий признак, по которому алгебраическая сумма двух действительных чисто иррациональных выражений может равняться рациональному выражению.
Согласно принятому выше условию, каждое в отдельности выражения (1) и (2) являются иррациональными. Поэтому, а также, исходя из условия выполнения равенства (3), полагаем:
![]() (4) и
(4) и 
![]() (5),
(5),
где ![]() – чисто иррациональное и
– чисто иррациональное и ![]() – рациональное выражения.
– рациональное выражения.
То есть каждое из двух чисто иррациональных выражений ![]() и
и 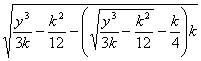 представим в виде суммы другого чисто иррационального выражения
представим в виде суммы другого чисто иррационального выражения ![]() и рациональных выражений, соответственно
и рациональных выражений, соответственно ![]() и
и ![]() . В этом случае их разность сохранит свое значение:
. В этом случае их разность сохранит свое значение: ![]() , (
, (![]()
![]() , обоснованность этого утверждения покажем ниже).
, обоснованность этого утверждения покажем ниже).
Найдем соответствующие заданным условиям значения ![]() и
и ![]() . Возведем оба выражения (4) и (5) во 2-ю степень, сложим и после преобразований получим:
. Возведем оба выражения (4) и (5) во 2-ю степень, сложим и после преобразований получим:
 (6). Находим корни данного квадратного уравнения:
(6). Находим корни данного квадратного уравнения:
![]()
 (7).
(7).
По условию ![]() – чисто иррациональное, следовательно, рациональная составляющая корней должна быть равна нулю:
– чисто иррациональное, следовательно, рациональная составляющая корней должна быть равна нулю: ![]() , отсюда
, отсюда ![]() (8) и
(8) и  (9). (Если же принять
(9). (Если же принять ![]() , то рациональная составляющая в выражении (7) не будет равна нулю, отсюда и
, то рациональная составляющая в выражении (7) не будет равна нулю, отсюда и ![]() не будет чисто иррациональным, что противоречит заданному условию –
не будет чисто иррациональным, что противоречит заданному условию – ![]() чисто иррациональное).
чисто иррациональное).
Выражения (4) и (5) примут вид:
![]() (10) и
(10) и 
![]() (11).
(11).
Выполним проверку полученных результатов, подставим найденные значения ![]() и
и ![]() в формулу (4)
в формулу (4) ![]() :
:
![]()

![]()
![]() , получили верное равенство.
, получили верное равенство.
При подстановке ![]() и
и ![]() в формулу (5)
в формулу (5) 
![]() также получим верное равенство, отсюда следует, что найденные значения
также получим верное равенство, отсюда следует, что найденные значения ![]() и
и ![]() верны.
верны.
Выполним еще одну проверку, используя равенства (10) и (11):

![]()

![]()
![]() .
.
Итак, в результате имеем верные равенства:
(10) ![]() , (11)
, (11)  .
.
Отсюда следует, что полученные выражения являются корнями квадратного уравнения вида
![]()
 (12),
(12),
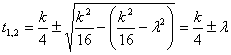 (13), где
(13), где ![]() является иррациональной составляющей корней квадратного уравнения, то есть является чисто иррациональным выражением.
является иррациональной составляющей корней квадратного уравнения, то есть является чисто иррациональным выражением.
Обобщим полученный результат. Пусть алгебраическая сумма двух чисто иррациональных выражений ![]() и
и ![]() равна рациональному выражению
равна рациональному выражению ![]()
![]() . Представим выражения
. Представим выражения ![]() и
и ![]() в следующем виде:
в следующем виде:
![]() (14) и
(14) и ![]() (15),где
(15),где ![]() − рациональное,
− рациональное, ![]() − чисто иррациональное выражения. В этом случае можно придти к исходному выражению:
− чисто иррациональное выражения. В этом случае можно придти к исходному выражению: ![]() . Возведем выражения (14) и (15) во вторую степень и сложим, получим:
. Возведем выражения (14) и (15) во вторую степень и сложим, получим: ![]() .
.
Корни данного уравнения  .
.
В силу того, что ![]() является чисто иррациональным выражением, рациональная составляющая корней должна равняться нулю:
является чисто иррациональным выражением, рациональная составляющая корней должна равняться нулю: ![]() , отсюда следует
, отсюда следует ![]() и соответственно получаем
и соответственно получаем ![]() и
и ![]() .
.
Покажем, что разложение чисто иррациональных выражений на алгебраические суммы другого чисто иррационального выражения и рационального является единственным.
Пусть в разложениях выражений ![]() и
и ![]() можно представить
можно представить ![]() в виде суммы других рационального
в виде суммы других рационального ![]() и чисто иррационального
и чисто иррационального ![]() выражений:
выражений: ![]() (16), отсюда
(16), отсюда ![]() (17) и
(17) и ![]() (18).
(18).
Возведем данные выражения во вторую степень, сложим и после преобразования получим ![]() (19),
(19),
откуда ![]() (20). Поскольку
(20). Поскольку ![]() − чисто иррациональное, то отсюда рациональная составляющая корней должна быть равна нулю:
− чисто иррациональное, то отсюда рациональная составляющая корней должна быть равна нулю: ![]() , в этом случае из формулы (16) получаем
, в этом случае из формулы (16) получаем ![]() . Таким образом, чисто иррациональные выражения могут быть представлены корнями квадратного уравнения единственным образом:
. Таким образом, чисто иррациональные выражения могут быть представлены корнями квадратного уравнения единственным образом:
![]() и
и![]() .
.
Вернемся к равенству (3): ![]()
 .
.
Зададим в данном выражении произвольные значения ![]() и
и ![]() , например,
, например, ![]() и
и ![]() . Подставим эти значения в выражения (10) и (11), выполним вычисления:
. Подставим эти значения в выражения (10) и (11), выполним вычисления:
а)![]() (21), откуда
(21), откуда ![]() ;
;
б) 
отсюда ![]() .
.
Вычислим ![]() , используя полученную выше формулу (9) :
, используя полученную выше формулу (9) :
 , подставим в данную формулу значения
, подставим в данную формулу значения ![]() и
и ![]() , получим:
, получим:
 .
.
Как видим, результаты всех произведенных вычислений совпадают, что позволяет заключить о правильности рассуждений.
Окончательно по результатам выполненных исследований делаем вывод:
Вывод: Для того чтобы алгебраическая сумма двух чисто иррациональных выражений ![]() и
и ![]() , где значения каждого из них являются действительными иррациональными числами, равнялась рациональному выражению
, где значения каждого из них являются действительными иррациональными числами, равнялась рациональному выражению ![]() :
: ![]() , необходимо и достаточно, чтобы данные выражения были однозначно представлены корнями квадратного уравнения:
, необходимо и достаточно, чтобы данные выражения были однозначно представлены корнями квадратного уравнения: ![]() и
и ![]() , или
, или ![]() и
и ![]() , где
, где ![]() – чисто иррациональное выражение.
– чисто иррациональное выражение.
Применение данного свойства рассмотрим на примере.
Пример 2.
Рассмотрим разность двух чисто иррациональных выражений: ![]() (21), где
(21), где ![]() и
и ![]() – рациональные, отличные от нуля числа,
– рациональные, отличные от нуля числа, ![]() , а значения каждого из слагаемых выражений являются иррациональными числами.
, а значения каждого из слагаемых выражений являются иррациональными числами.
Выполним проверку, может ли ![]() являться рациональным выражением. Отметим внешний признак − второе слагаемое выражение входит в состав первого, то есть является сложным выражением.
являться рациональным выражением. Отметим внешний признак − второе слагаемое выражение входит в состав первого, то есть является сложным выражением.
Предположим, что ![]() − рациональное.В таком случае, согласно сделанного выше вывода, оба чисто иррациональные выражения должны являться корнями квадратного уравнения:
− рациональное.В таком случае, согласно сделанного выше вывода, оба чисто иррациональные выражения должны являться корнями квадратного уравнения:
![]() (22) и
(22) и ![]() (23), где
(23), где ![]() − чисто иррациональное выражение. Отсюда будем иметь выполнение равенства (21)
− чисто иррациональное выражение. Отсюда будем иметь выполнение равенства (21)
![]() . Из (22) и (23) получим
. Из (22) и (23) получим ![]()
![]() (27).
(27).
Корнями данного уравнения будут ![]() (28).
(28).
Поскольку ![]() − чисто иррациональное, рациональная составляющая корней должна равняться нулю
− чисто иррациональное, рациональная составляющая корней должна равняться нулю ![]() , отсюда следует
, отсюда следует ![]() . Но это условие невыполнимо, так как при любых
. Но это условие невыполнимо, так как при любых ![]() и
и ![]() всегда
всегда ![]() . Отсюда следует, что иррациональные выражения (22) и (23) нельзя представить в виде корней квадратного уравнения.
. Отсюда следует, что иррациональные выражения (22) и (23) нельзя представить в виде корней квадратного уравнения.
Таким образом, достаточное условие равенства алгебраической суммы двух чисто иррациональных выражений рациональному выражению не выполняется, отсюда следует, что ![]() − иррациональное.
− иррациональное.
Попытаемся ответить на поставленный вопрос другим способом.
Возведем выражение ![]() в третью степень, получим:
в третью степень, получим:
![]() (29).
(29).
Приходим к кубичному уравнению относительно ![]() :
:
![]() .
.
Решение данного уравнения даст значения ![]() выраженное через радикалы, могут ли эти значения быть рациональными, однозначно ответить сложно или невозможно.
выраженное через радикалы, могут ли эти значения быть рациональными, однозначно ответить сложно или невозможно.
Примечание:
Какие-либо литературные источники по заявленной теме мною не использованы.