Цели:
- Развитие интереса к изучению предмета математика.
- Отработка навыков слухового восприятия.
- Воспитание коллективизма, чувства долга и ответственности каждого за всех.
Оборудование: ножницы, бумага А4, ручки, 6 стаканов.
Подготовительная работа:
- Турнир проводится в конце «Недели математики».
- Каждая команда должна выпустить математическую газету, приготовить форму одежды, придумать название команды, эмблему, девиз, приветствия соперникам и жюри.
- Учащиеся знакомятся самостоятельно с историей математики, биографией и интересными фактами ученых математиков.
- Каждая команда готовит номер художественной самодеятельности, содержащую связь с математикой.
- Члены жюри выбираются из приглашенных (3 человека).
План мероприятия:
1. Оргмомент (1–2 мин.)
2. Турнир «Приветствие».
3. Турнир «Математический комплимент».
4. Турнир «Разминка».
5. Турнир «Экскурсия в историю».
6. Турнир «Практика».
7. Музыкальный турнир.
8. Турнир «Подсказка».
9. Подведение итогов.
ХОД УРОКА
I. Оргмомент
Ведущий. Добрый вечер учащиеся, учителя и гости. Мы сегодня проводим Математический турнир между командами мальчиков и девочек 7 и 8 классов. В словаре русского языка турнир – это состязание, соревнование в чем-либо. Наши команды будут соревноваться своей сообразительностью, быстротой ума, внимательностью, знанием математики и ее истории, умением слушать и слышать.
Представление жюри и жеребьевка для первого турнира.
II. Турнир «Приветствие»
Ведущий. Объявляется первый турнир «Приветствие». Каждая команда должна себя представить: назвать команду, рассказать о значении эмблемы команды, девиз, приветствие соперникам и приветствие жюри.
Команда девочек «Пифагор».
Девиз: «Всегда и везде Пифагор на высоте».
Приветствие сопернику: « «Пифагор» лучше всех, нам сопутствует успех, утомленным математикам «Пифагор» шлет привет».
Приветствие жюри: «Пифагоры» - супердети, это знают все на свете; Пифагоры лучшим судьям шлют огромнейший привет».
Команда мальчиков «ЛОМ» (Любим очень математику ).
Девиз: «Одна голова хорошо, а восемь лучше».
Приветствие соперникам:
«Желаем вам, желаем вам…
Чтоб лучший приз достался нам».
Приветствие жюри:
«О! Члены жюри! Мы приветствуем Вас!
И просим: не строго судите Вы нас!
И если вдруг в знаниях будет прокол
Не стоит язвительный делать укол.
Пусть добрая шутка порадует Вас,
А вы, улыбнувшись, воскликните «Класс!»
III. Турнир «Математический комплимент»
Ведущий. Всем нам нравится, когда нас осыпают комплиментами, похвалой. Каждой команде предоставляется шанс задобрить жюри математическими комплиментами. Это значит, в комплименте должны содержаться математические термины.
IV. Турнир « Разминка»
Ведущий. Объявляется турнир « Разминка». Задание общее для каждой команды. Я читаю текст задачи, вы слушаете внимательно, и записываете ответ на листке бумаги, после короткого совещания. Всего 3 задачи.
Задача 1.
Имеются песочные часы на 3 минуты и 7 минут. Надо опустить яйцо в кипящую воду ровно на 4 минуты. Как это сделать? (Поставить часы одновременно, когда 3 минуты пройдет, опустить яйцо.)
Задача 2.
60 листов книги имеют толщину 1 см. Какова толщина всех листов, если в книге 240 страниц? (Ответ: 2 см)
Задача 3.
Требуется полсотни разделить на половину. Сколько получится? (Ответ: 50 : 1/2 =100)
V. Турнир «Экскурсия в историю»
Ведущий. Каждый человек по своему уникален, а ученые математики тем более: они и астрономы, и поэты, и физики, и художники. Одним словом – незаурядные личности. Некоторые факты из жизни ученых-математиков передаются из уст в уста веками. Сейчас я приведу краткую информацию о трех великих математиках. Вы должны узнать о ком идет речь, записать их имена на листочке по порядку и сдать ответы жюри.
Первая история
Им написано около 1000 работ почти по всем основным разделам математики. Он отличался исключительной работоспособностью. Его вычислительные способности заменяли счетную машину. В 1735 году он в 3 дня выполнил большую вычислительную работу, которая лишь посильна только большому коллективу квалифицированных счетных работников и то в течении нескольких месяцев. Но от перенапряжения после этой работы он ослеп на один глаз. В 1766 году он ослеп и на второй глаз. Но и слепой, он продолжал свои открытия. После его смерти осталось очень много рукописей, которые Петербургская академия печатала в течении 47 лет. О ком идет речь? (Леонард Эйлер)
Вторая история
Крупнейший немецкий математик. В раннем детстве проявлял необыкновенные способности к изучению математики. Трех лет от роду этот математик исправил ошибку в расчетах отца, начислявшего недельный заработок рабочим своей бригады. Учитель на одном из уроков арифметики предложил третьеклассникам найти сумму всех натуральных чисел от 1 до 100. По установленному порядку, решивший задачу первым, клал свою аспидную доску на середину стола. Туда и положил он свое решение, едва только учитель договорил последние слова формулировки задачи. Его решение было верным и оригинальным. О ком идет речь? (Карл Гаусс.)
История третья
Он родился во Франции в маленьком городе Бур-Лярен 26 октября 1811 года. Заложил основы современной алгебры. Он дважды представлял в Парижскую академию наук свои работы. Однако даже такие крупные математики, как Коши и Фурье, не оценили его выводов и затеряли рукописи. Из-за сжатости изложения и новизны идей его работы долгое время не получали признания. Лишь через 14 лет после его смерти они были опубликованы, а применение его идеи нашли еще позже. Все его литературное наследие умещается на нескольких десятках страниц, но из идей, которые в них содержатся, выросла целая библиотека. Он был убит на дуэли на 21-ом году жизни. О ком идет речь? (Эварист Галуа)
VI. Турнир «Практика»
Ведущий. Говорят, что теория без практики мертва, практика без теории глупа. Каждой команде представляется возможность доказать, что они справятся с любой задачей.
Задача 1.
Возьмите лист бумаги и ножницы. В этой маленькой бумаге надо сделать такое отверстие, чтобы через него можно было пролезть взрослому человеку. Как это сделать?
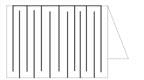
(Надо сложить лист пополам, делать надрезы. 1. Начиная с краю со стороны загиба, не доходя до конца. 2. Продолжаем в шахматном порядке, каждый раз не доводя до конца. 3. Последний надрез должен быть со стороны загиба, с другого края. 4. Затем прорезать линию сгиба, оставляя края.)
Задача 2.
Два стакана стоят недалеко друг от друга. Накрываем их листком бумаги. Теперь на эту бумагу надо сверху поставить еще один стакан. Можно ли сделать так, чтобы он удержался на бумаге между двумя стаканами, не соприкасаясь со стаканами? Если да, то как это сделать? (Бумажный лист должен быть гофрированным)
VII. «Музыкальный турнир»
Ведущий. Каждая команда должна была подготовить художественный номер, связанный с математикой, математическими понятиями. Даем слово команде «ЛОМ».
Звучит песня на мотив мелодии из кинофильма «Красная шапочка».
Если долго, долго, долго
Если долго и упорно,
Ежедневно и задорно
Математику учить,
Сколько ты всего узнаешь,
Тайн, загадок разгадаешь,
Образованнее станешь,
Только-только не ленись!
Припев:
А-а! правила учи ты!
А-а! формулы зубри ты!
А-а! не ленись, все повторяй!
А-а! ничего не забывай!
Ну, конечно, ну, конечно,
Если ты такой ленивый,
Если ты такой трусливый,
Ничего не хочешь знать!
Не решить тебе задачи,
Не решить тебе примера,
Станет для тебя проблемой
Математику учить!
Припев:
А-а! правила учи ты!
А-а! формулы зубри ты!
А-а! не ленись, все повторяй!
А-а! ничего не забывай!
И, наверно, верно-верно,
Заниматься очень трудно
И мучительно, и нудно,
Только ты не отступай!
Ты иди своей дорогой
До конца с наукой в ногу.
Будет все тебе понятно,
Интересно, так и знай!
Выступает команда девочек «Пифагор» с песней «Дважды два – четыре».
VIII. Турнир «Подсказка»
Ведущий. В каждом вопросе речь идет о каком-либо объекте, имеющем отношение к математике. Команды по очереди называют свои версии, но после каждой подсказки количество баллов, которые можно получить, уменьшается на два. За ответ с первой попытки команда может получить 10 баллов.
1. Речь идет о единице измерения длины:
- Первоначально определяли как длину трех ячменных зернышек.
- Означает первую фалангу большого пальца рук.
- Одна из основных английских мер длины.
- Равна 25, 4 мм.
- Имя одной из героинь сказок Андерсена произошло от названия этой меры длины.
Ответ: дюйм.
2. Этого нет у окружности:
- Это есть у правильного n-угольника.
- Может использоваться для нахождения площади.
- Их не может быть меньше двух.
- Может являться осью симметрии.
- У параллелограмма они пересекаются и точкой пересечения делятся пополам.
Ответ: диагональ.
3. Это приспособление для счета:
- Не нужны батарейки.
- Просты в обращении.
- Всегда перед глазами.
- Без этого трудно первокласснику.
- Пять братьев в одном чулане живут.
Ответ: пальцы.
4. Это функция:
- Область определения и область значения – все действительные числа.
- График пересекает хотя бы одну из осей координат.
- Для построения графика достаточно двух точек.
- Графиком является прямая.
- Функция задается формулой у = kх + b.
Ответ: линейная.
IX. Подведение итогов. Награждение победителей