В контрольно-измерительные материалы ЕГЭ включены задачи по стереометрии. В каждой задаче рассматривается, какое либо геометрическое тело.
От учащихся требуются умения применять изученные определения и теоремы с учётом знаний свойств геометрических тел. Вот почему так важны задачи, требующие “воображаемых построений”. Они часто служат основой для решения многих других задач, в частности таких, в которых требуется произвести построения на проекционном чертеже, когда точки, прямые и плоскости задаются с помощью призмы или пирамиды. Эти последние, в свою очередь, могут служить наглядной иллюстрацией первых
Рассмотрим конкретные примеры (формулировки задач, взятых из учебных пособий, несколько видоизменены).
Задача 1. Через точку М провести прямую, пересекающую две скрещивающиеся прямые b и а; М € а, М € b.
Решение. Пусть с — искомая прямая. Тогда
пересекающиеся прямые а и с определяют
проходящую через них плоскость 
, a прямые b и с — проходящую через них
плоскость 
. Так как М 
с, с = 
, то М
и М .
Таким образом, если задача имеет решение, то
искомая прямая c = 
, где = (M, а), = (М, b).
На рис. 1 искомая прямая с пересекает прямые а и b в точках X и Y (рис.1).
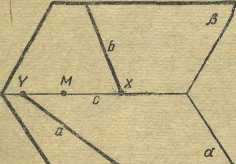
Р и с. 1
Исследование. Было установлено, что
искомая прямая есть линия пересечения
плоскостей и . (Отсюда не следует, что искомую
прямую можно провести только с помощью
плоскостей и , дальше будет дано другое решение.)
Это значит, что любая прямая, отличная от линии
пересечения плоскостей и , не может быть решением
задачи. Плоскости и не могут совпадать, так как
прямые а и b не лежат в одной
плоскости. Кроме того, М т. E 
есть
прямая. Отсюда следует, что задача имеет не более
одного решения. Может оказаться что, а || c или b
|| c, тогда задача не имеет решения.
Задача 1 учащимся дается нелегко, Им трудно
представить себе взаимное расположение прямых а,
b, с и плоскостей и , поэтому решение лучше
иллюстрировать на модели. Задать точку М и
прямые а, b, например, с помощью тетраэдра (рис.
2).
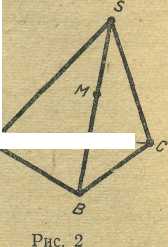
Р и с. 2
Пусть точка М принадлежит ребру SB тетраэдра SABC. Нужно провести прямую, проходящую через точку М и, пересекающую скрещивающиеся прямые SA и ВС.
Легко заметить, что решением задачи будет
прямая SB. Выясняем ее свойства: (SB) = (SAB)
(SBC), т. Е.
(SB) — линия пересечения плоскостей и , где
плоскость проходит через
точку М и прямую SA, а плоскость — через точку М и другую прямую ВС.
Излагая построение в общем виде, можно выполнить рис. 1.
При исследовании важно добиваться четкого ответа на следующие вопросы:
- Откуда следует, что задача имеет не более одного решения?
- При каком условии задача имеет решение?
Несмотря на то что с = g p, всегда существует, задача
может не иметь решения. Почему?
Можно ли задать точку М и прямые а, b, чтобы задача не имела решений?
Для того чтобы учащиеся лучше поняли решение задачи 1, целесообразным не раз возвращаться к приведенному выше общему случаю, дополняя его конкретным заданием точки М и прямых а, b, как это сделано в задачах 1.1 —1.3.
Задача 1.1. Дана пирамида SABCD и точка
М; М
[SA]. Через точку М провести прямую,
пересекающую прямые SB и CD.
Решение. Анализ. Как было показано (задача
1), искомой прямой может быть только линия
пересечения плоскостей = (MSB)
и = (MCD). Для ее
построения достаточно найти точку пересечения
прямой CD с плоскостью
(рис. 3).
Построение.
1) (АВ) (CD = X, X = (CD)
MSB);
2) (MX)—искомая прямая.
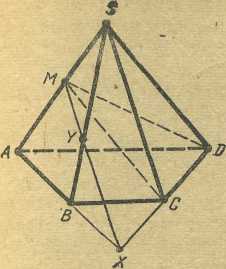
Р и с. 3
Задача 1.1 подсказывает другое решение задачи 1.
Пусть плоскость проходит
через точку М и прямую a, прямая b пересекается
с плоскостью в точке X
(рис.1). Искомой прямой будет (MX), если (МХ) не есть пустое множество. На
рис. 1 (МХ) = Y. Для
того чтобы найти точку X, достаточно через
прямую b провести произвольную плоскость z. Пусть
d — линия пересечения плоскостей z и , тогда X=bd.
В задаче 1.1: а = (SB), b = (CD), = (MSB), z = (ABCD), d = (AB).
Следует обратить внимание учащихся на два вывода, полученные при решении задачи 1 двумя способами:
- Если задача 1 имеет решение, то искомая прямая c= .
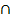
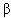- Если задача 1 имеет решение, то искомая прямая с
= (MX), где X=b 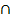a.
Учащимся полезно понять, что эти два
высказывания не противоречат друг другу, так как = (МХ).
Задача 1.2. Дана пирамида SABCD. Через
точку М [SD] провести прямую, пересекающую
прямые SB и AC.
Решение. Для построения искомой прямой
достаточно найти точку пересечения прямой АС с
плоскостью = (SBD). Строим
точку X (рис. 4), где Х= (AC) (BD). Тогда Х== (AC) и (MX) —искомая прямая,
если (MX) (SB) не есть пустое множество.
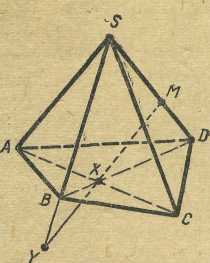
Рис. 4
Задача 1.3. Дан параллелепипед ABCDA1B1C1D1
и точка MlB1C1]. Построить прямую,
проходящую через точку М и пересекающую
прямые АВ и СС1.
Решение. Прямая MB — искомая (рис.5).
Действительно: (MB) (AB)=B, (MB) (СС1)=Х.
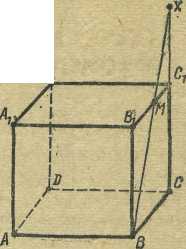
Рис. 5
Задача 1.4. Дан параллелепипед ABCDA1B1C1D1
и точка M [C1C]. Построить прямую,
проходящую через точку М и пересекающую
прямые АВ и A1D1.
Анализ. Воспользовавшись вторым решением
задачи 1, заключаем, что искомой прямой будет (MX),
где X=(A1D1) (MBA).
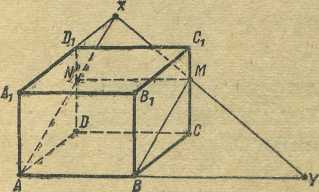
Р и с. 6
Построение (рис. 6).
1) (AN) = (MBA
1D1D), N [DD1];
2)
(AN) (A1D1),
X = (A1D1) (MBA);
3) (MX) – искомая прямая. На рис. 6: (MX) (A1D1)
= X, (MX)
(AB) = Y
Исследование. При любом выборе точки М между точками С1 и С задача имеет решение.
Вот примеры ещё двух задач. За каждой из них следуют две задачи на построение, на которых удобно иллюстрировать общий случай.
Задача 2. Проведите прямую, параллельную прямой а и пересекающую две скрещивающиеся прямые b и с.
Задача 2.1. Дан параллелепипед ABCDA1B1C1D1. Построить прямую, параллельную (A1D1) и пересекающую (В С) и (А1В1).
Задача 2.2. Дан параллелепипед ABCDA1B1C1D1 . Построить прямую, параллельную (А1С1) и пересекающую (ВB1) и (AD).
Задача 3. Через данную точку провести прямую, параллельную двум данным пересекающимся плоскостям.
Задача 3.1. Дана пирамида SABCD и точка
М [SD]. Через
точку М провести прямую, параллельную
плоскостям SAB и SCD.
Задача 3.2. Дан параллелепипед ABCDA1B1C1D1. Через вершину А1 провести прямую, параллельную плоскостям AB1D 1 и BB1C1C.
Опыт показал, что, несмотря на усвоение учащимися решений задач 1–3 в общем виде, частные случаи представляют определённый интерес при подготовке к ЕГЭ: решения таких задач для учащихся обычно не очевидны, связаны с преодолением некоторых трудностей и развивают пространственные представления. С другой стороны, эти задачи помогают выработать умения применять изученные определения и свойства геометрического тела. Устанавливается преемственность между задачами на доказательства и задачами на построение сечений призм и пирамид, создаются благоприятные условия для выработки навыков в решении конструктивных задач по стереометрии.
При подготовке статьи я использовала следующую литературу:
- Л. С. Атанасян, В. Ф. Бутузов и др. Геометрия 10-11 класс М. Просвещение, 2006 г.
- А. Г. Погорелов. Геометрия 7-11 класс М. Просвещение, 2002 г.
- К. С. Барыбин. Геометрия 10-11 класс М. Просвещение, 2000 г.
- Л. Силаев. Динамика геометрических фигур. М. Чистые пруды, 2007 г.
- Г. И. Глейзер. История математики в школе. М. Просвещение, 1992 г.