Функция занимает одно из ведущих мест в школьном курсе алгебры и имеет многочисленные приложения в других науках. В начале изучения, с целью мотивации, актуализации вопроса сообщаю, что ни одно явление, ни один процесс в природе не могут быть изучены, никакая машина не может быть сконструирована, а затем действовать без полного математического описания. Одним из инструментом для этого является функция. Её изучение начинается в 7-м классе, как правило, дети не вникают в определение. Особенно труднодоступными понятиями являются такие как область определения и область значения. Используя, известные связи между величинами в задачах на движение, стоимости перекладываю их на язык функции, удерживая связь с её определением. Таким образом, у учащихся понятие функции формируется на осознанном уровне. На этом же этапе ведётся кропотливая работа над новыми понятиями: область определения, область значения, аргумент, значение функции. Использую опережающее обучение: ввожу обозначения D(у), Е(у), знакомлю с понятием нуля функции (аналитически и графически), при решении упражнений с участками знакопостоянства. Чем раньше и чаще учащиеся встречаются с трудными понятиями, тем лучше их осознают на уровне долговременной памяти. При изучении линейной функции целесообразно показать связь с решением линейных уравнений и систем, а позднее с решением линейных неравенств и их систем. На лекции учащиеся получают большой блок (модуль) новой информации, поэтому в конце лекции материал " отжимается" и составляется конспект, который учащиеся должны знать. Практические навыки отрабатываются в процессе выполнения упражнений с применением различных методов, в основе которых индивидуальная и самостоятельная работа.
1. Некоторые сведения о линейной функции.
Линейная функция очень часто встречается в практической деятельности. Длина стержня является линейной функцией температуры. Длина рельсов, мостов также является линейной функцией температуры. Расстояние, пройденное пешеходом, поездом, автомашиной при постоянной скорости движения, – линейные функции времени движения.
Линейная функция описывает ряд физических зависимостей и законов. Рассмотрим некоторые из них.
1) l = lо(1+at) – линейное расширение твёрдых тел.
2) v = vо(1+bt) – объёмное расширение твёрдых тел.
3) p=pо(1+at) – зависимость удельного сопротивления твёрдых проводников от температуры.
4) v = vо + at – скорость равноускоренного движения.
5) x= xо+ vt – координата равномерного движения.
Задача 1.
Определите линейную функцию по табличным данным:| х | 1 | 3 |
| у | -1 | 3 |
Решение. у= kx+b, задача сводится к решению системы уравнений: 1=k•1+b и 3=k•3 + b
Ответ: у = 2х – 3.
Задача 2.
Двигаясь равномерно и прямолинейно, тело прошло за первые 8с 14м, а ещё за 4с – 12 м. Составьте по этим данным уравнение движения.Решение. По условию задачи имеем два уравнения: 14= хо+8•vо и 26=хо+12•vо, решая систему уравнений, получаем v=3, хо =-10.
Ответ: х = -10 + 3t.
Задача 3.
Из города вышел автомобиль, движущийся со скоростью 80км/ч. Через 1,5 ч вдогонку ему выехал мотоцикл, скорость которого 100 км/ч. Через сколько времени мотоцикл его догонит? На каком расстоянии от города это произойдёт?Ответ: 7,5ч, 600км.
Задача 4. Расстояние между двумя точками в начальный момент 300м. Точки движутся навстречу друг другу со скоростями 1,5 м/с и 3,5м/с. Когда они встретятся? Где это произойдёт?
Ответ: 60 с, 90 м.
Задача 5. Медная линейка при 0 о С имеет длину 1м. Найдите увеличение её длины при повышении её температуры на 35 о, на 1000 о С (температура плавления меди 1083 о С)
Ответ:0,6мм.
2. Прямая пропорциональность.
Многие законы физики выражаются через прямую пропорциональность. В большинстве случаев для записи этих законов используется модель
у=кх
в отдельных случаях –
к=у/х.
Приведём несклько примеров.
1. S = v•t (v – const)
2. v = a•t (a – const, a – ускорение).
3. F = kx (закон Гука:F – сила, к– жёсткость(const), х– удлинение).
4. Е= F/q (Е– напряженность в данной точке электрического поля, Е – const, F– сила, действующая на заряд, q – величина заряда).
В качестве математической модели прямой пропорциональности можно использовать подобие треугольников или пропорциональность отрезков (теорема Фалеса).
Задача 1.
Поезд проехал мимо светофора за 5 с, а мимо платформы длиной 150 м, за 15 с. Каковы длина поезда и его скорость?Решение. Пусть х – длина поезда, х+150 – суммарная длина поезда и платформы. В данной задаче скорость постоянна, а время пропорционально длине.
Имеем пропорцию: (х+150) :15 = х : 5.
Откуда х = 75, v = 15.
Ответ. 75 м, 15 м/с.
Задача 2. Катер прошел по течению 90 км за некоторое время. За то же время он прошел бы против течения 70 км. Какое расстояние за это время проплывет плот?
Ответ. 10 км.
Задача 3. Какова была первоначальная температура воздуха, если при нагревании на 3 градуса его обьём увеличился на 1% от первоначального.
Ответ. 300 К (Кельвин) или 270С.
Лекция по теме "Линейная функция".
Алгебра, 7 класс
1. Рассмотрим примеры задач с применением известных формул:
S = v·t (формула пути), (1)
С = ц·к (формула стоимости). (2)
Задача 1. Автомобиль отъехав от пункта А на расстояние 20км продолжил свой путь со скоростью 62 км/ч. На каком расстояние от пункта А будет находиться автомобиль через t часов? Составьте выражение к задаче, обозначив расстояние S, найдите его при t = 1ч, 2,5 ч, 4ч.
Решение.
1) Используя формулу (1) найдём путь, пройденный
автомобилем со скоростью 62 км/ч за время t, S1
= 62t;
2) Тогда от пункта А через t часов автомобиль
будет находиться на расстояние S = S1 + 20
или S = 62t + 20, найдём значение S:
при t = 1, S = 62*1 + 20,
S = 82;
при t = 2,5, S = 62*2,5 + 20, S = 175;
при t = 4, S = 62*4+
20, S = 268.
Замечаем, что при нахождении S меняется только значение t и S, т.е. t и S – переменные, причём S зависит от t, каждому значению t соответствует единственное значение S. Обозначив, переменную S за Y, а t за x, получим формулу для решения данной задачи:
Y= 62х + 20. (3)
Задача 2. В магаине купили учебник за 150 рублей и 15 тетрадей по n рублей. Сколько денег уплатили за покупку? Составьте выражение к задаче, обозначив стоимость С, найдите его при n = 5,8,16.
Решение.
1) Используя формулу (2) найдём стоимость
тетрадей С1 = 15n;
2) Тогда стоимость всей покупки С= С1+150
или С= 15n+150, найдём значение C:
при n = 5, С = 15•5 + 150,
С= 225;
при n = 8, С = 15•8 + 150,
С= 270;
при n = 16, С = 15•16+
150, С= 390.
Аналогично, замечаем, что С и n переменные, для каждого значения n соответствует единственное значение С. Обозначив, переменную С за Y, а n за x, получим формулу для решения задачи 2:
Y= 15х + 150. (4)
Сравнивая формулы (3) и (4) убеждаемся, что переменная Y находится через переменную х по одному алгоритму. Мы рассмотрели лишь две разные задачи, описывающие окружающие нас явления каждый день. На самом деле процессов, изменяющих по полученным законам – множество, поэтому такая зависимость между переменными заслуживает изучение.
Решения задач показывают, что значения переменной х выбраны произвольно, удовлетворяющие условиям задач (положительные в задаче 1 и натуральные в задаче 2), т. е. х – независимая переменная (её называют аргументом), а Y – зависимая переменная и между ними однозначное соответствие, а по определению такая зависимость является функцией. Следовательно, обозначив коэффициент при х буквой k, а свободный член буквой b, получим формулу
Y= kx + b.
Определение.
Функция вида y= kx + b, где k, b – некоторые числа, х - аргумент, y– значение функции, называется линейной функцией.Для изучения свойств линейной функции введём определения.
Определение 1. Множество допустимых значений независимой переменной, называется областью определения функции (допустимые – это значит те числовые значения х при которых выполняются вычисления y) и обозначается D(у).
Определение 2. Множество значений зависимой переменной, называется областью значения функции (это те числовые значения, которые принимает y) и обозначается Е(у).
Определение 3. Графиком функции называется множество точек координатной плоскости, координаты которых обращают формулу в верное равенство.
Определение 4. Коэффициент k при х называется угловым коэффициентом.
Рассмотрим свойства линейной функции.
1. D(у) – все числа (умножение определено на
множестве всех чисел).
2. Е(у) – все числа.
3. Если y = 0, то х = -b/k, точка (-b/k;0) – точка
пересечения с осью Ох, называется нулём функции.
4. Если х= 0, то y= b, точка (0;b) – точка
пересечения с осью Оу.
5. Выясним, в какую линию выстроит точки
линейная функция на координатной плоскости, т.е.
что является графиком функции. Для этого
рассмотрим функции
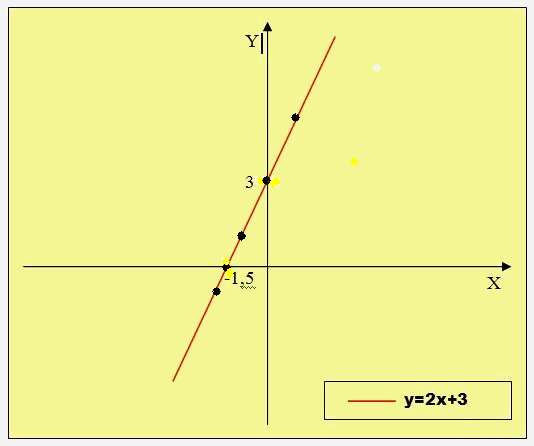
1) y= 2x + 3, 2) y= -3x – 2.
Для каждой функции составим таблицу значений. Зададим произвольные значения переменной х, и вычислим соответствующие значения переменной Y.
1)
| х | -1,5 | -2 | 0 | 1 | 2 |
| Y | 0 | -1 | 3 | 5 | 7 |
2)
х |
-2/3 |
-2 |
0 |
1 |
2 |
Y |
0 |
4 |
-2 |
-5 |
-8 |
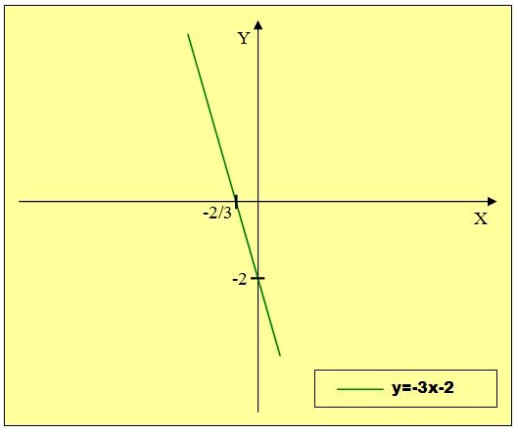
Построив полученные пары (х;y) на координатной плоскости и соединяя их для каждой функции отдельно (мы взяли значения х с шагом 1, если уменьшить шаг, то точки выстроятся чаще, а если шаг будет близок к нулю, то точки сольются в сплошную линию), замечаем, что точки выстраиваются в прямую линию в случае 1) и в случае 2). В силу того, что функции выбраны произвольно (постройте самостоятельно графики y= 0,5x – 4, y= x + 5), сделаем вывод, что графиком линейной функции является прямая. Используя свойство прямой: через две точки проходит единственная прямая, достаточно для построения прямой взять две точки.
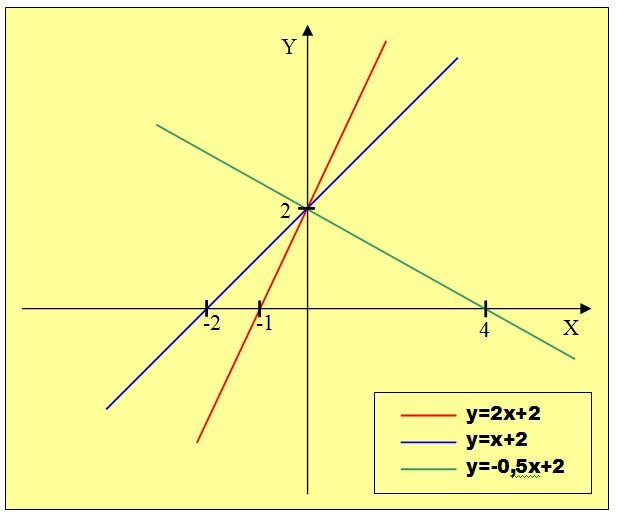
6.Из геометрии известно, что прямые могут либо пересекаться, либо быть параллельными. Исследуем взаимное расположение графиков нескольких функций.
1) y= -x + 5, y= -x + 3, y= -x – 4; 2) y= 2x + 2, y= x + 2, y= -0,5x + 2.
Построим группы графиков 1) и 2) и сделаем выводы.
|
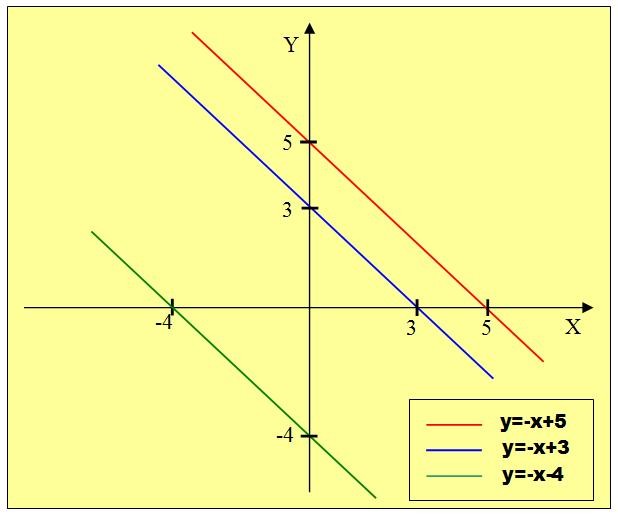 |
Графики функций 1) расположились параллельно, исследуя формулы, замечаем, что все функции имеют одинаковые коэффициенты при х.
Графики функций 2) пересеклись в одной точке (0;2). Исследуя формулы, замечаем, что коэффициенты различны, а число b = 2.
Кроме этого, нетрудно заметить, что прямые, заданные линейными функциями с k › 0 образуют с положительным направлением оси Ох – острый угол, с k ‹ 0 тупой угол. Поэтому коэффициент k называется угловым коэффициентом.
7. Рассмотрим частные случаи линейной функции, в зависимости от коэффициентов.
1) Если b=0, то функция принимает вид y= kx, тогда k = y/х (отношение показывает, во сколько раз отличается или какую часть составляет y от х).
Функцию вида Y= kx, называют прямой пропорциональностью. Эта функция обладает всеми свойствами линейной функции, её особенностью является то , что при х=0 y=0. График прямой пропорциональности проходит через начало координат точку (0;0).
2) Если k = 0, то функция принимает вид y = b, что означает, при любых значениях х функция принимает одно и то же значение.
Функцию вида y = b, называют постоянной. Графиком функции является прямая проходящая через точку (0;b) параллельно оси Ох, при b=0 график постоянной функции совпадает с осью абсцисс.
Конспект
1. Определение Функция вида Y= kx + b, где k, b – некоторые числа, х -аргумент, Y– значение функции, называется линейной функцией.
D(у) – все числа.
Е(у) – все числа.
Графиком линейной функции является прямая, проходящая через точку (0;b).
2. Если b=0,то функция принимает вид y= kx, называется прямой пропорциональностью. График прямой пропорциональности проходит через начало координат.
3. Если k = 0, то функция принимает вид y= b, называется постоянной. График постоянной функции проходит через точку (0;b), параллельно оси абсцисс.
4. Взаимное расположение графиков линейных функций.
Даны функции y= k1x + b1 и y= k2x + b2.
Если k1= k2, то графики параллельны;
Если k1и k2 не равны, то графики пересекаются.
5. Примеры графиков линейных функций см. выше.
Литература.
- Учебник Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков и другие. “Алгебра, 8”.
- Дидактические материалы по алгебре для 8 класса / В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк. – М.: Просвещение, 2006. – 144 с.
- Приложение к газете 1 сентября “Математика”, 2001 г., №2, №4.