Цель урока:
- Образовательная: систематизировать теоретические и практические знания учащихся при исследовании функции на монотонность, на экстремумы, исследование функции на наибольшее и наименьшее значения функции на промежутке, составление уравнения касательной, составление уравнения касательной параллельной данной
- Развивающая: способствовать развитию математической речи, оперативной памяти, произвольного внимания, наглядно-действенного мышления.
- Воспитательная: развивать у учащихся коммуникативные компетенции (умение работать в группе, культуру общения), способность к самооценке на основе критерия успешности учебной деятельности, способствовать развитию интеллектуальной деятельности учащихся,
Задачи урока:
- образовательная: углубление и систематизация теоретических знаний, отработка умений и навыков при решении упражнений;
- развивающая: развитие самостоятельности, потребности к самообразованию, к активной творческой деятельности;
- воспитательная: воспитание чувства ответственности, культуры общения, уважения друг к другу, взаимопонимания, уверенности в себе;
Тип занятия: повторения и систематизации знаний по теме “Применение производной для исследования функции”.
Структура урока
1. Постановка целей и задач урока.
2. Актуализация знаний:
а) тест
б) блиц-опрос.
в) самостоятельная работа
3. Практическое применение теоретических знаний.
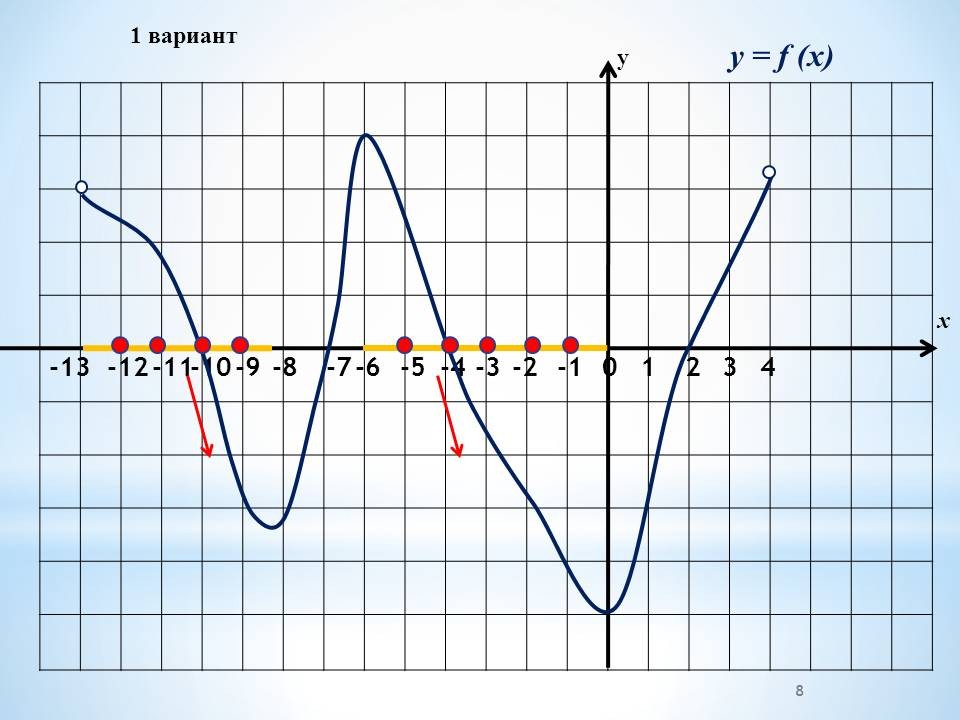
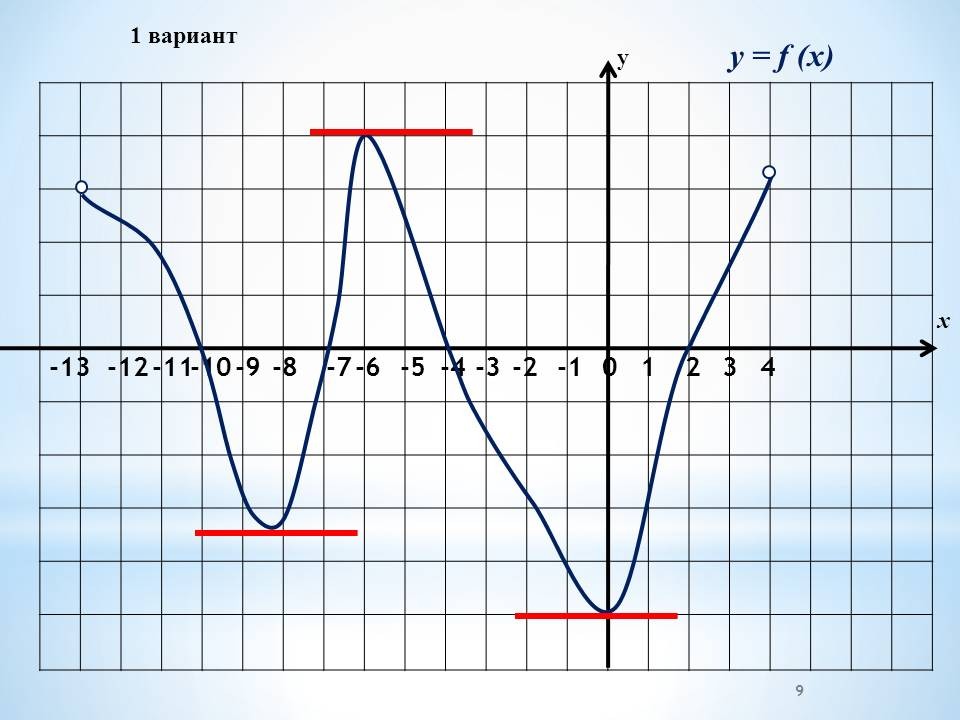
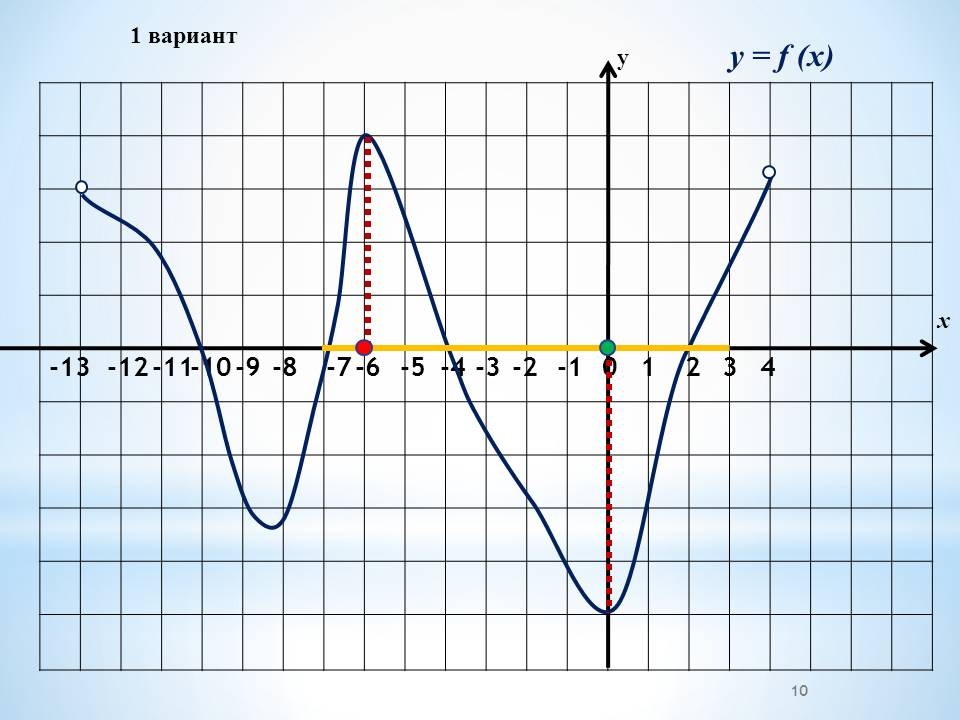
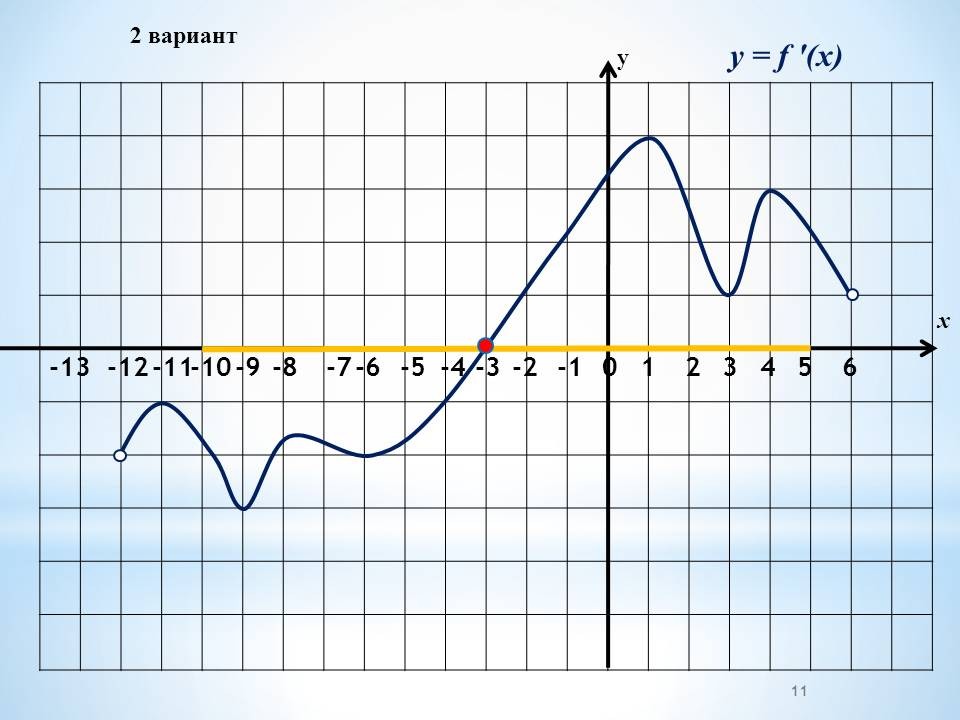
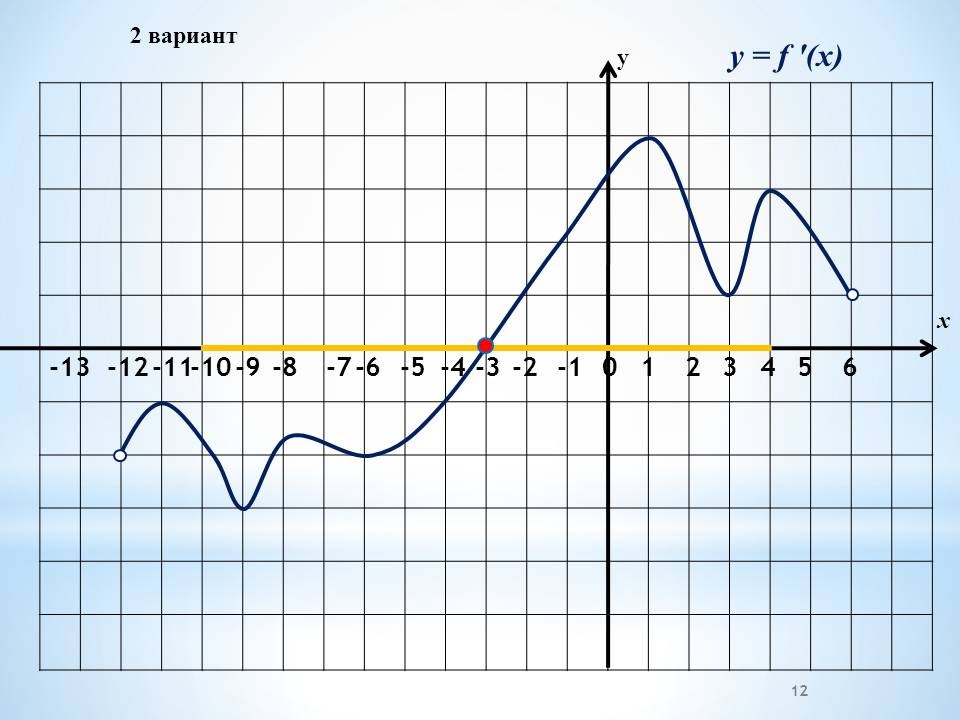
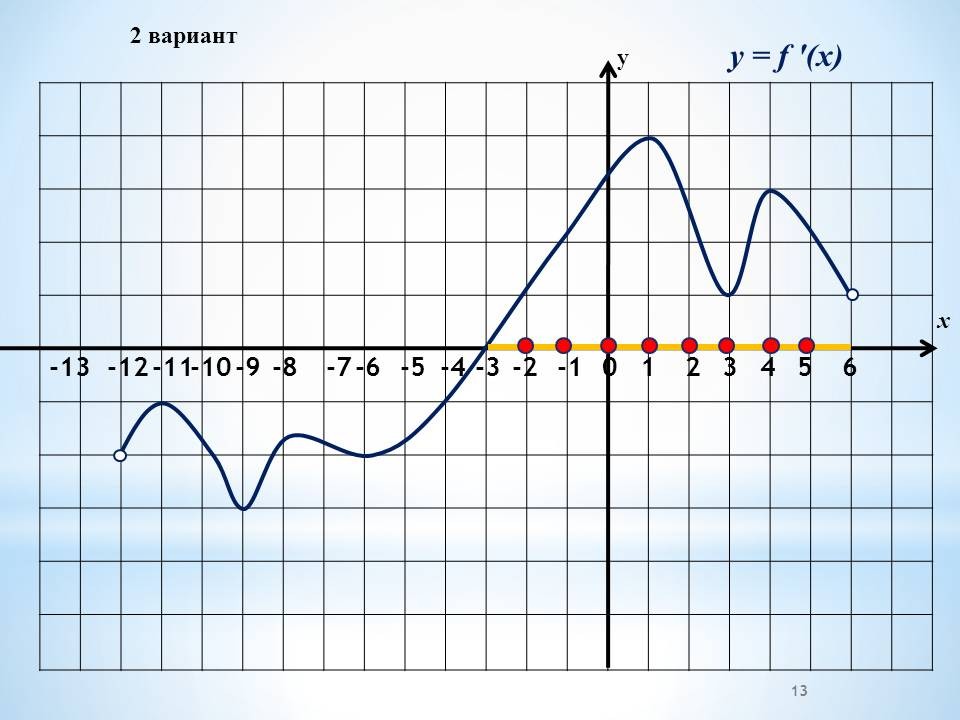
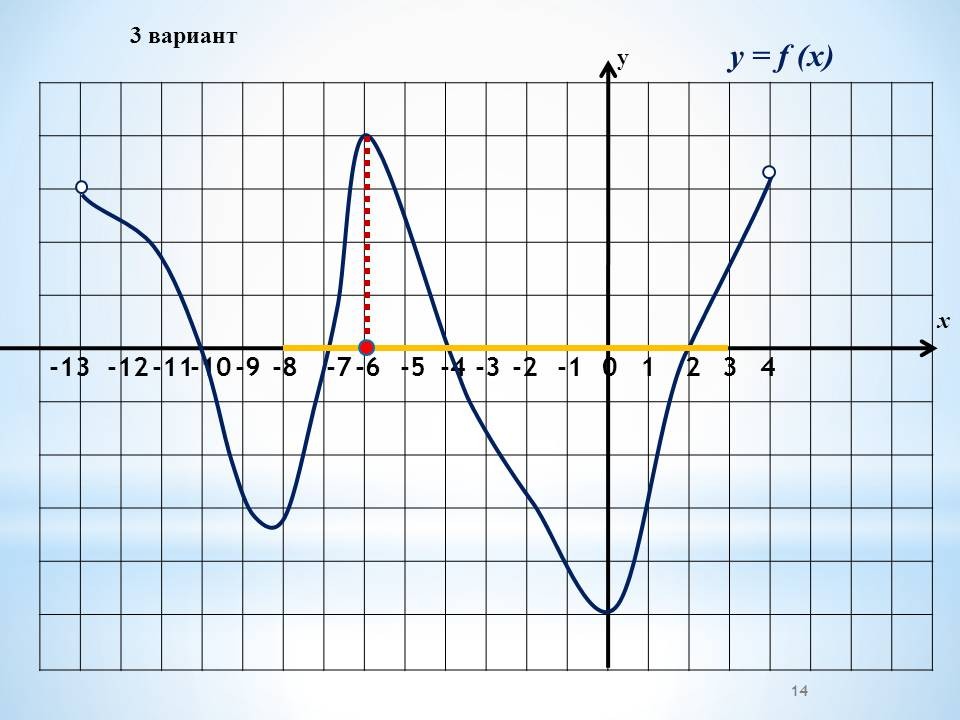
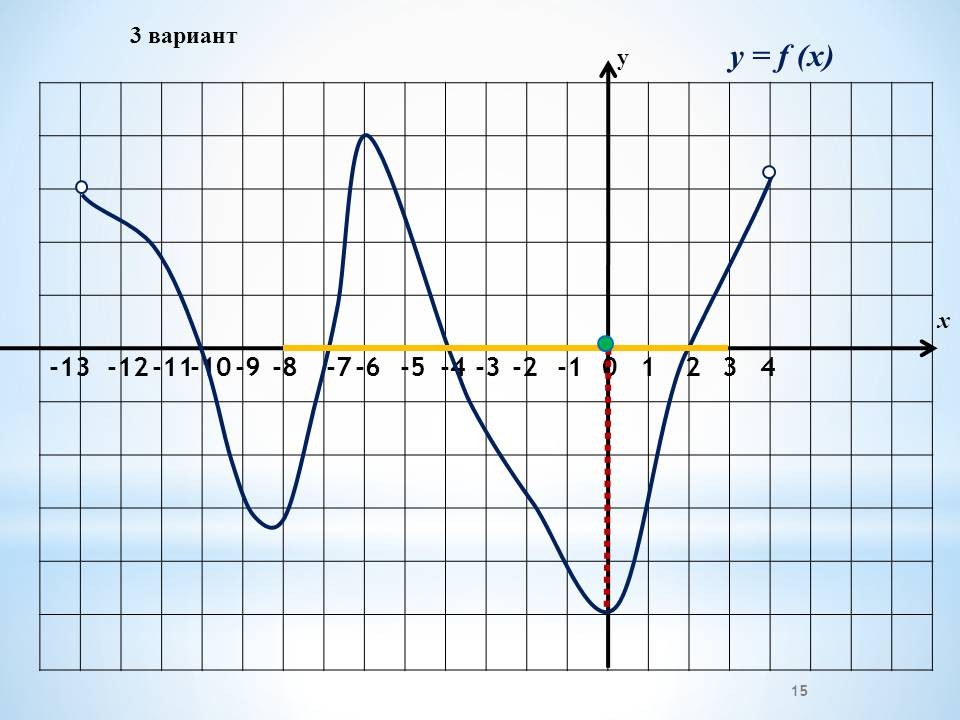
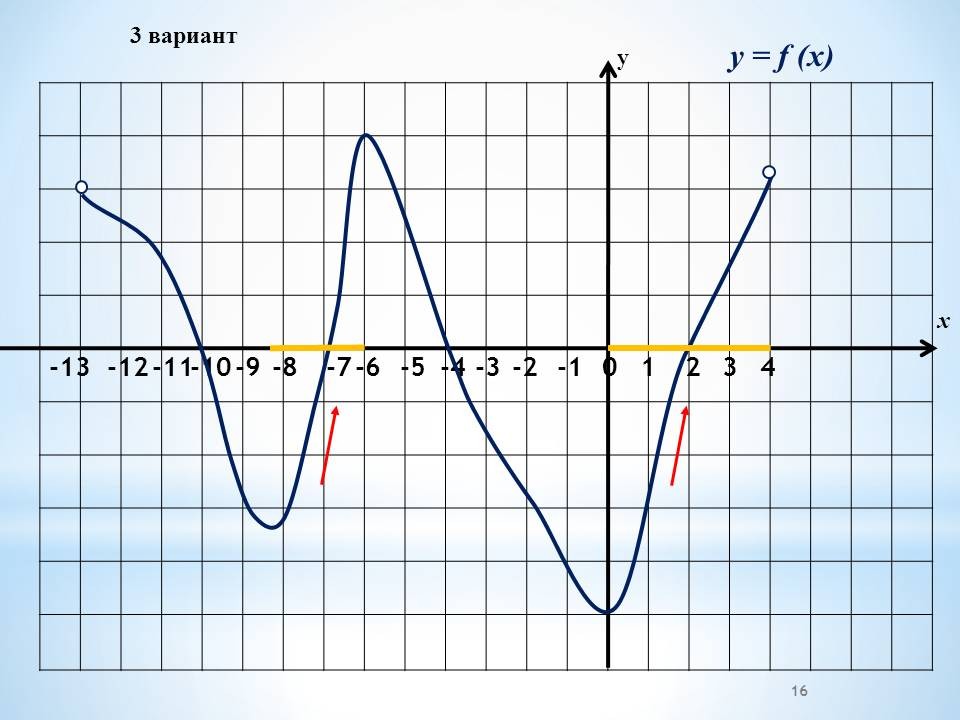
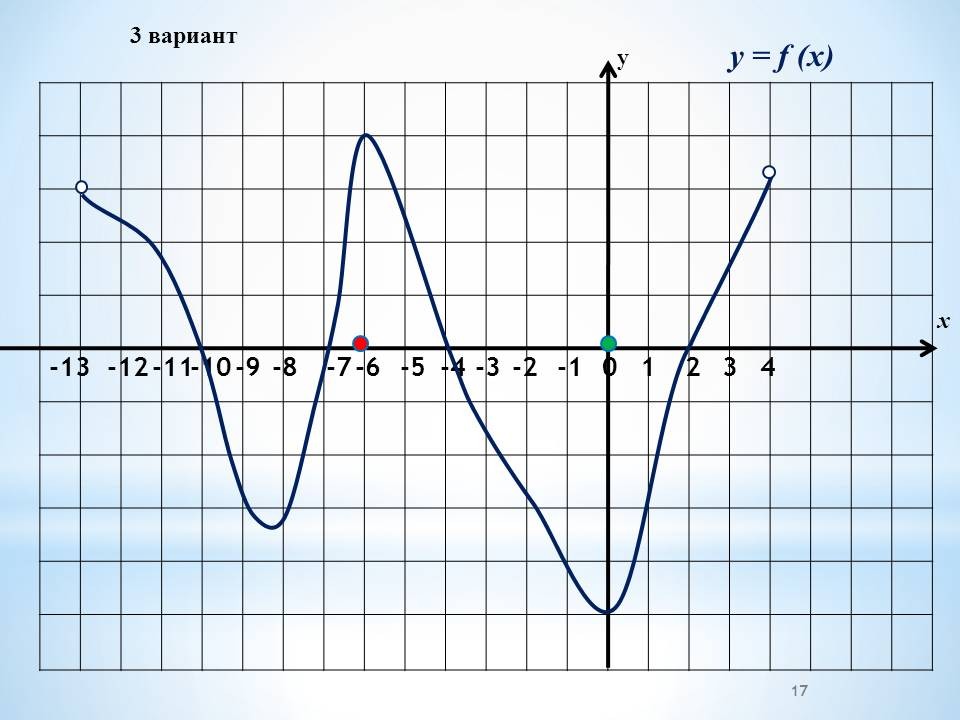
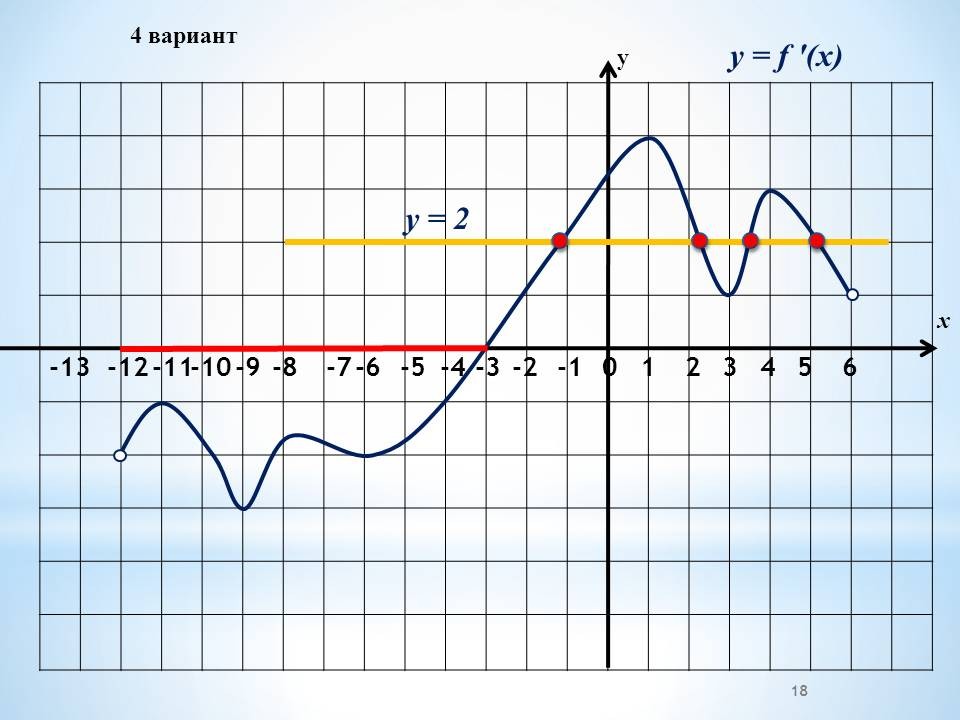
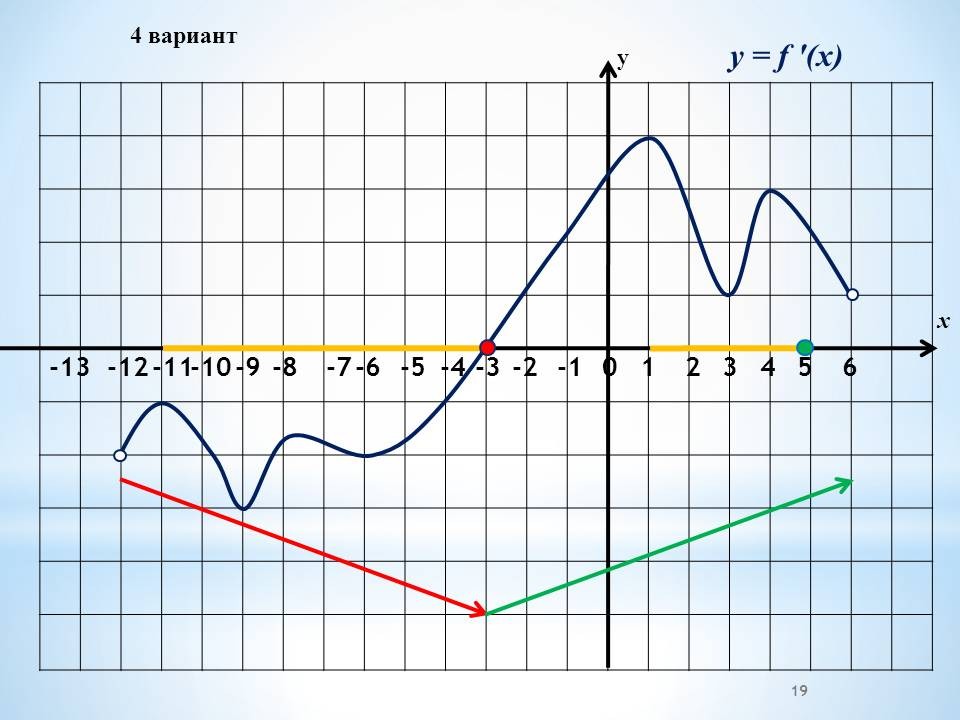
а) Работа в группах по графикам функций, графикам производной функции.
Проведение инструктажа учащихся по проведению работы в группах. Класс изначально делится на 4 группы. Каждая группа получает задание. Учащиеся работают в группах, обсуждают решение. 4 варианта заданий с графиками функций и графиками производных и вопросы к ним.
б) Защита работ по группам
в) Предлагается вспомнить алгоритмы применения производной к исследованию функций. (на экстремумы; на наибольшее и наименьшее значения функции на промежутке, на составление уравнения касательной, на составление уравнения касательной параллельной данной прямой)
г) Работа у доски, по одному человеку от группы.
д) Организуется проверка решений.
4. Подведение итогов. Выставление оценок. Рефлексия.
5. Задание на дом
Формы работы учащихся: фронтальная, индивидуальная, групповая
Необходимое оборудование: раздаточный материал, доска, экран, проектор
Ход урока
1. Организационный момент
Объявление тему урока, постановка целей и задач урока.
Здравствуйте, ребята! Сегодня мы с вами проведём урок по теме:
“Производная и её применение для исследования функций”. Как вы думаете, какие цели мы поставим перед собой? (повторить наши теоретические знания о правилах вычисления производной, о применении производной к исследованию функций)
В процессе работы вы должны показать уровень усвоения теоретического материала, навыки применения его при решении задач, умение выступать перед аудиторией.
2. Актуализировать знания и умения уч-ся, которые будут использованы на уроке
Для того чтобы проверить ваши знания по правилам дифференцирования, проведем тест из которого узнаем кому принадлежат следующие высказывания.
а) тест;
Слайд 4.
Предлагаю вам узнать, кому принадлежат высказывания.
1. Математику уж затем учить следует, что она ум в порядок приводит
2. В математике есть тоже своя красота, как в живописи и поэзии
Для этого вам необходимо установить соответствие между заданиями и буквами с ответами.
(1 вариант - Ломоносов, 2 вариант – Жуковский)
2 варианта теста, в каждый включены 9 заданий на нахождение производной функции.
Каждому варианту ответа соответствует буква. По окончании теста учащиеся определят фамилию автора, которому принадлежит высказывание.
б) блиц-опрос
Учитель задаёт вопросы классу.
Слайд 6.
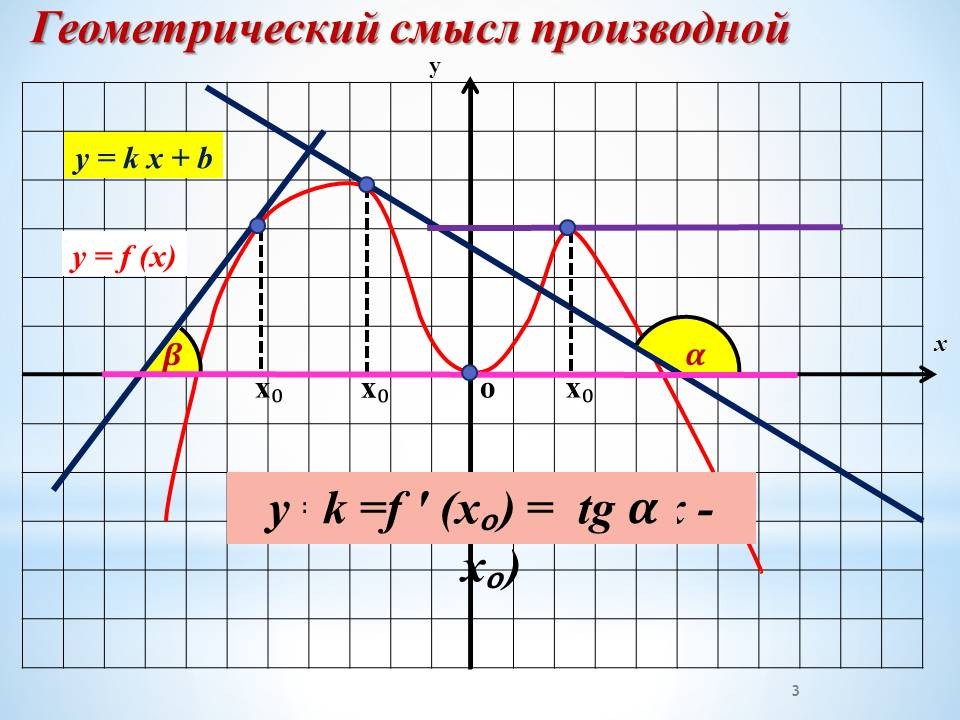
- В чем заключается геометрический смысл производной?
- Как выглядит уравнение касательной к графику функции y=f(x) в точке с абсциссой x0 в общем виде?
- Знание углового коэффициента касательной к графику функции позволяет ответить на некоторые вопросы при исследовании функции.
- Уравнение касательной (прямой) имеет вид у= kx + b, где k – угловой коэффициент, который характеризует угол, образованный прямой с положительным направлением оси Ох.
- Какие значения принимает k, если угол образованный прямой с положительным направлением оси Ох, тупой? (k <0)
- Какие значения принимает k, если угол образованный прямой с положительным направлением оси Ох, острый? (k >0)
- Какие значения принимает k, если угол образованный прямой с положительным направлением оси Ох, равен нулю? (k =0)
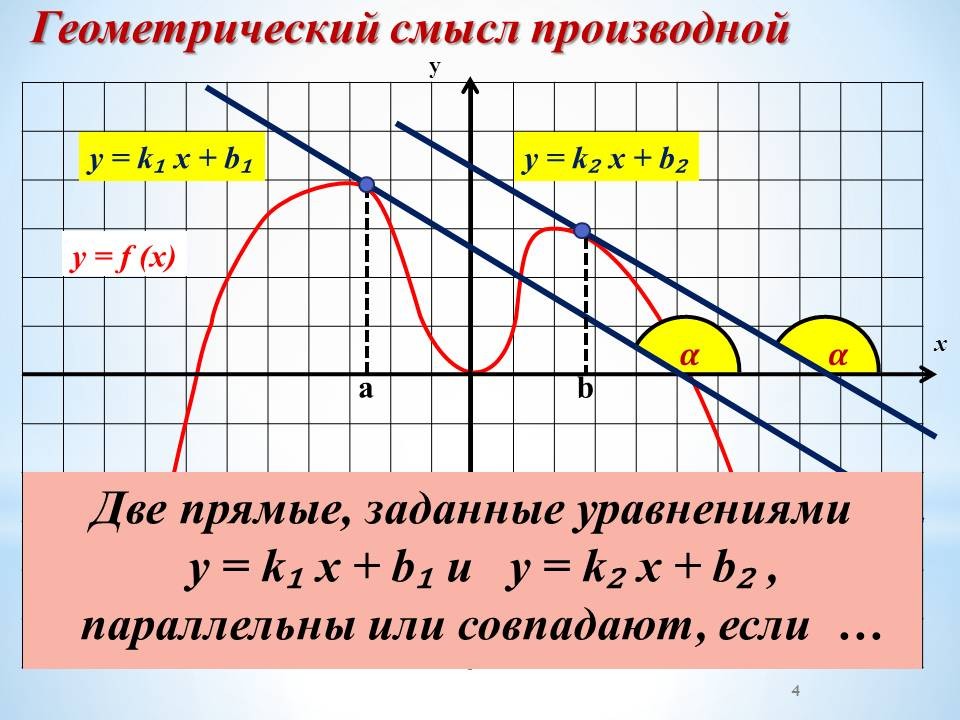
Слайд 7.
В каком случае две прямые, заданные уравнениями y = k1 x + b1 и y = k2х + b2, параллельны или совпадают? (k1=k2).
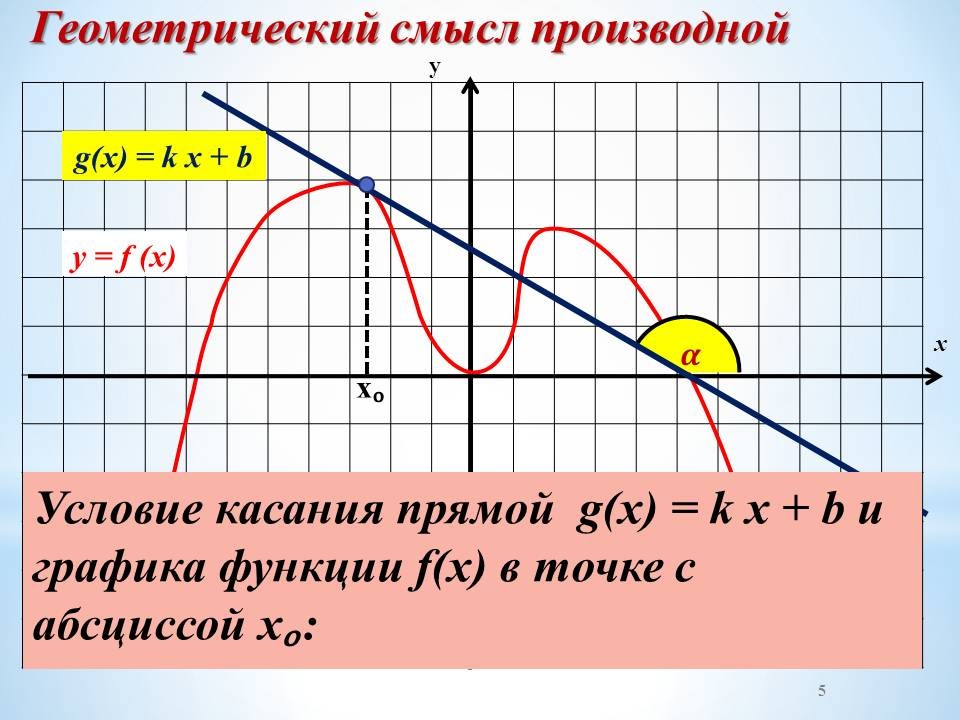
Слайд 8.
При каких условиях прямая g(x) = kx + b является касательной к графику функции у=f(x)?
в) Самостоятельная работа (2 варианта)
Чтобы показать зависимость свойств функции и производной, выполним самостоятельную работу. Организует самопроверку правильности выполнения.
Учащиеся выполняют самостоятельную работу в тетрадях по вариантам на соответствие свойств функции и производной. Самостоятельно проверяют правильность выполнения заданий.
3. Практическое применение теоретических знаний (чередование индивидуальной и групповой форм работы с последующей проверкой задания)
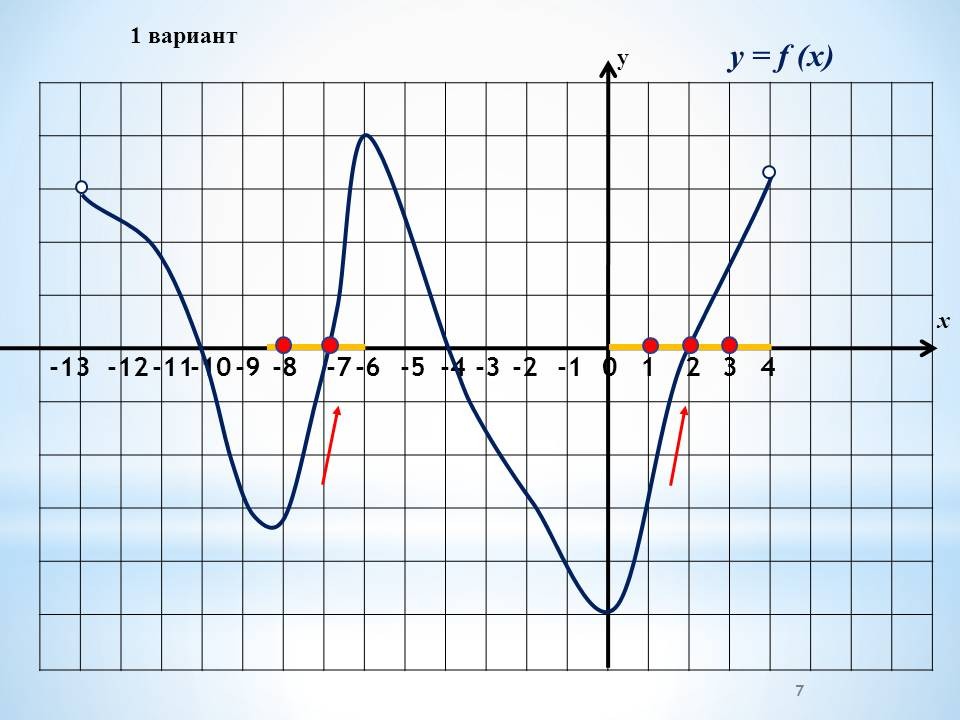
а) Работа в группах по готовым графикам функций, графикам производной функции. (3 минуты)
На данном этапе работы нам предстоит ответить на вопросы, используя график
функции, или график производной функции.
Проведение инструктажа учащихся по проведению работы в группах. Каждая группа получает один из вариантов. В два варианта включены графики функций и 4 вопроса по графикам. Другие два варианта содержат графики производных, 4 вопроса к ним Учащиеся работают в группах, обсуждают решение.
б) Защита задания по группам.
Каждая группа по очереди дает ответ на предложенное задание и объясняет выбор ответа.
в) Предлагается вспомнить алгоритмы применения производной при исследовании функции на экстремумы, наибольшее и наименьшее значения функции, на составление уравнения касательной и выполнить практические задания.
- 1 группа – исследование функции на экстремумы
- 2 группа – исследование функции на наибольшее и наименьшее значения на промежутке
- 3 группа – составление уравнения касательной
- 4 группа - составление уравнения касательной параллельной данной прямой
д) Организует проверку выполнения заданий
Опрос по графикам функций и графикам производной.
4. Подведение итогов. Выставление оценок. Рефлексия деятельности на уроке
Вопросы учителя учащимся.
- Получилось ли у вас повторить и систематизировать знания по данной теме?
- Оцените свою работу на занятии.
- Какое у вас настроение в конце занятия?
5. Домашнее задание. № 1955, №1987, 2000
Приложения