“Недостаточно лишь понять задачу,
необходимо желание решить её.
Без сильного желания решить
трудную задачу невозможно,
но при наличии такого – возможно.
Где есть желание, найдется путь”.
Д.Пойа
Не всегда уравнения разрешают сомнения,
по итогам сомнения может быть озарение!
Изменение приоритетных направлений развития современной системы образования ставит перед школой задачу формирования творческой личности, способной ориентироваться в многообразии окружающего мира. Функционально грамотная личность – это человек, принимающий решения и выстраивающий линию своего поведения и, как следствие, свою жизнь в целом, с высокой степенью самостоятельности.
Качественное изменение социального заказа общества, потребность в творчески мыслящих людях, обладающих нестандартным взглядом на проблемы, определило задачу развития гибкости мышления учащихся.
То есть новые условия жизни обуславливают новые требования к уровню образования современного школьника. Они-то и учтены в стандарте нового поколения (ФГОС), который определяет требования к достижению предметных, метапредметных и личностных образовательных результатов обучающихся.
Все это предполагает формирование компетенций или универсальных учебных действий (УУД), среди которых важнейшее место занимают познавательные УУД. Одной из составляющих этой группы являются логические УУД, формируемые в определения понятий, обобщения, нахождении аналогии, выявления причинно-следственных связей, выстраивание логических цепочек умозаключений.
Во все времена в нашей стране для системы математического образования существенное значение имело развитие интеллектуального потенциала подрастающего поколения. “Нагрузку”, связанную с развитием логического мышления, прежде всего, берёт на себя математика, хотя, как известно, большинство из школьных наук в той или иной степени так же формируют логическое мышление.
Если мы хотим целенаправленно развивать интеллектуальные умения, основывающиеся на таких приемах мыслительной деятельности как анализ, синтез, аналогия, обобщение, классификация, гибкость и вариативность мышления, то очевидно необходима специально выстроенная методика, направленная на формирование и развитие логических приемов умственных действий.
Такие умения относятся к решению арифметических текстовых задач, и, особенно нестандартных, которые в свою очередь являются неотъемлемой частью современного урока математики. Решение таких задач с определенной периодичностью позволяет приучать школьников к правильности и четкости рассуждений, развивает гибкость ума, избавляет от стандартного алгоритмического мышления.
Я предлагаю сначала методически разобрать такой урок поэтапно на примере задачи, решаемой инверсией или “с конца”.
Этап 1.
Уже с 5-ого класса при проведении фактически каждого из уроков у учителя есть несколько минут при актуализации темы и постановке целей, чтобы тем или иным способом рассказать учащимся интересные факты, относящиеся к предмету или предстоящей теме урока. Эта информация хотя и носит развивающий характер, но целенаправленно побуждает к активной мыслительной деятельности.
Не менее важен сам процесс урока, где ребята учатся анализировать, рассуждать логически и делать выводы.
Этап 2.
Практически все математические задания в той или иной степени формируют логическое мышление, однако есть ряд специальных заданий, которые целенаправленно развивают умение строить цепочки логических рассуждений, используя математические сведения. Их можно использовать как разминку перед чтением и решением нестандартной текстовой задачи. Приведу примеры некоторых известных задач.
Разминка. Устные упражнения.
Вы – шофер автобуса. В автобусе первоначально было 23 пассажира. На первой остановке вышло 3 женщины и зашло 5 мужчин. На второй остановке зашло 4 мужчины и вышло 7 женщин. Сколько лет шоферу?
Какое слово из 11 букв все отличники пишут неправильно?
Продавая в магазине попугая, продавец пообещал, что попугай будет повторять каждое услышанное им слово. Покупатель очень обрадовался, но придя домой, обнаружил, что попугай “нем как рыба”. Тем не менее, продавец не лгал. Как это могло быть?
Английский офицер, вернувшийся из Китая, заснул в церкви во время службы. Ему приснилось, что к нему приближается палач, чтобы отрубить ему голову, и тот самый момент, когда сабля опускалась на шею несчастного, его жена, желая разбудить заснувшего, слегка дотронулась до его шеи веером. Потрясение было столь велико, что офицер тут же умер. В этой истории, рассказанной вдовой офицера, что-то неладно. Что же именно?
Петя решил купить Маше мороженое, но для его покупки ему не хватало 3 рублей, а Маше всего лишь 1 рубля. Тогда они решили сложить свои деньги, но опять не хватило 1 рубля на покупку даже одного мороженного.Сколько стоила порция мороженого?
Этап 3.
Одно из необходимых умений, которое важно для правильного решения текстовых задач – это внимательное чтение условия задачи.
Умеем ли мы читать? Каждый из нас даст утвердительный ответ.
Умеем ли мы читать внимательно? Каждый из нас наверняка задумается, и большая часть даст утвердительный ответ.
Умеем ли мы читать внимательно и выполнять предложенное задание? Каждый из нас задумается, и только некоторая часть даст утвердительный ответ. Следовательно, актуальной задачей каждого педагога является научить внимательному чтению поставленного условия, и как следствие в дальнейшем успешной работы. Что впоследствии приведет к умению точно исполнять предложенную инструкцию, что немаловажно при сдаче экзаменов в форме ОГЭ и ЕГЭ для каждого ученика.
Этап 4.
Начинать с ребятами решение задач инверсией, наверное, надо с более красочной и занимательной задачи, используя перед чтением короткую логическую разминку. Исходя из требований ФГОС и приоритета развивающего и проблемного обучения, задача разбирается послайдовым чтением, начиная с постановки проблемы.
Приведу пример на своей авторской задаче из урока, предложенного ниже.
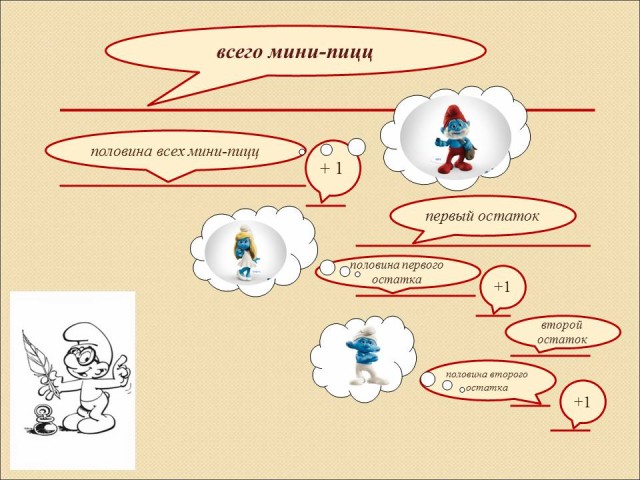
Задача: Смурфик Повар по особому рецепту испек любимые мини-пиццы смурфиков. Папе Смурфу он отнес половину приготовленных мини-пицц и еще одну мини-пиццу. Красотке Смурфетте он преподнес половину остатка и еще одну мини-пиццу, а Ворчуну досталась половина последнего остатка и последняя мини-пицца. Сколько мини-пицц испек Повар по тайному рецепту? (слайды 6-10, Презентация 1)
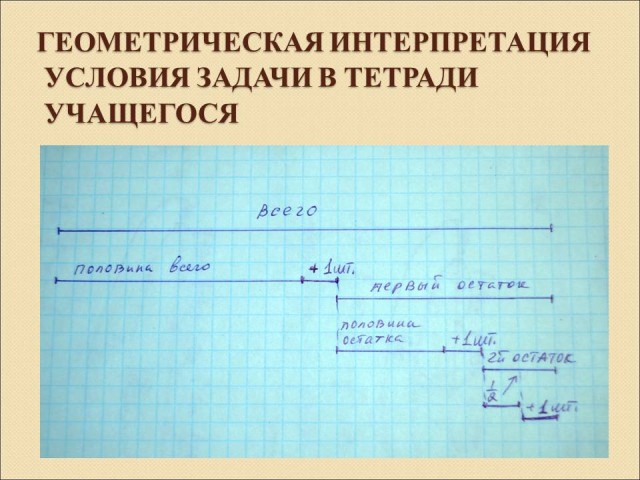
Решение лучше всего начинать геометрической интерпретацией задачи (решение “в отрезках”). (Слайд 11 Презентация 1)
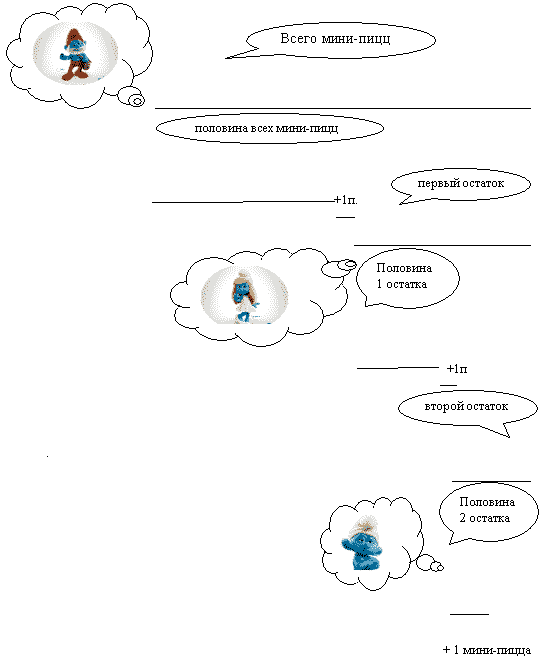
У каждого ученика на столе есть раздаточный материал с задачей и ее геометрической интерпретацией (Приложение 1), но до определенного момента лист перевернут напечатанным вниз.
Важно не только показать задачу на слайдах, но и начертить в отрезках на доске вместе с ребятами (они чертят в тетради)! (Слайд 12 Презентация 1– для проверки). После этого можно перевернуть листы, лежащие на партах и еще раз (при выведенном на экран соответствующем слайде) проговорить с учащимися этапы решения задачи. Далее, после обсуждения, решаем.
Половина второго остатка составляет 1 мини-пицца, следовательно,
- 1 + 1 = 2 мини-пиццы составляют второй остаток,
- 2 + 1 = 3 мини-пиццы составляют половину первого остатка,
- 3 + 3 = 6 мини-пицц составляют первый остаток,
- 6 + 1 = 7 мини-пицц составляют половину всего,
- 7 + 7 = 14 мини-пицц было всего.
Ответ: Смурфик Повар испек всего 14 мини-пицц.
Этап 5.
Делается вывод о том, что, решая “с конца”, последовательно пришли к тому, что было в самом начале. Прием используется, когда в задаче известно число, полученное в конце выполнения каких-либо действий.(Слайд 13 Презентация 1).
Нужно помочь учащимся осознать некоторые способы, приемы, общие подходы к решению нестандартных арифметических задач. Сформулированные рекомендации по решению нестандартных задач объединяются в следующей известной памятке.
Памятка.
Если тебе трудно решить задачу, то попробуй:
1) сделать к задаче рисунок или чертеж; подумай, может быть нужно сделать для них дополнительные построения или изменить чертеж в процессе решения задачи;
2) начать решение задачи “с конца”;
3)ввести вспомогательный элемент (часть);
4) переформулировать задачу другими словами, чтобы она стала понятной и знакомой;
5) разделить условие или вопрос задачи на части и решить ее по частям;
6)использовать для решения задачи способ подбора.
Важно объяснить детям, что данные указания носят рекомендательный характер. Необязательно применять их в той последовательности, как они записаны в памятке, необязательно выполнять все рекомендации при решении одной задачи, можно комбинировать их в разных сочетаниях. В этом суть творческого процесса решения нестандартных задач. Можно показать это учащимся при совместном решении нескольких задач и на разных уроках.
В моем пособии “Материалы в помощь учителю математики для 5-6 классов (с авторским курсом наглядно-практической геометрии)”, изданным еще в 2000 г. на страницах 136-142 вы также можете найти задачи, решаемые инверсией. Там каждая задача дана с решением тремя способами: геометрически, по действиям и уравнением. Скачать пособие бесплатно, а так же еще много интересных книг можно на моем личном сайте http://matematix.ru/
Ниже, приведено словесное описание урока (Презентация 1) на заявленную тему и подборки задач, решаемых инверсией (Приложение 2 и Приложение 3). Естественно, они будут рассмотрены и решены ни на одном занятии. Формируя логическое мышление своих учеников, к ним имеет смысл возвращаться на других уроках, в следующих классах по мере изучения новых тем. Таких как “Десятичные дроби”, “Проценты”, “Приведение дробей к общему знаменателю”, “Решение задач уравнениями” и т.д.
Урок математики в 5 классе на тему“Решение задач на части с конца"
Оборудование:
- На доске написано высказывание: “Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия” (Д. Пойа) и русская народная пословица “Ум без догадки гроша не стоит”. (Презентация 1. Слайд 2)
- На проекционной доске слайд с портретом Джорджа Пойа и обложкой его книги “Как решить задачу”.(Слайд 3)
- Отпечатанные условия задач для каждого ученика.
- Лист с пропечатанной основой для решения задачи про Смурфиков (Приложение 1).
- Карточки для устной работы.
- Проектор.
- Карточка с задачами для домашней работы (Задачи, собранные в подборку моей коллегой Мушинской А.В. Приложение 2. Или из моего пособия “Материалы в помощь учителю математики для 5-6 классов (с авторским курсом наглядно-практической геометрии)”, стр.136-142, http://matematix.ru/).
Цели урока:
- Углубить, упрочить полученные знания и навыки в решении задач на части. Обобщить и систематизировать знания и умения учащихся по теме “Нахождение целого по его части”.
- Актуализация опорных знаний в условиях решения нестандартной задачи.
- Формирование приемов умственной деятельности, развитие логического мышления.
- Развитиеумениярешатьзадачиспомощьючертежа, безсоставленияуравнений.
Ход урока
I. Вступительное слово учителя (Слайд 2)
Решение задач – практическое искусство, подобное плаванию, катанию на лыжах или игре на фортепиано, научиться ему можно. “Если вы хотите плавать, смело входите в воду, а если хотите научиться решать задачи, то решайте их”, – советовал учащимся известный американский математик Джордж Пойа в книге “Как решить задачу”. (Слайд 3)
Решение любой достаточно трудной задачи требует напряженного труда, воспитывает волю, упорство, развивает любознательность, смекалку.
Это нужные качества в жизни человека, ведь даже в пословице говорится: “Ум без догадки гроша не стоит”.А увлечение математикой часто начинается с размышлений над какой-то новой, интересной, нестандартной и понравившейся задачей.
II. Повторение теоретического материала
Далее учитель вместе с учениками ставит цель урока и переходит к работе по теории.
- Что такое дробь?
- Какие виды дробей вы знаете?
- Что показывает числитель и знаменатель обыкновенной дроби?
- Как найти часть от числа?
- Как найти целое, зная его часть?
Эти теоретические знания будут использованы для решения задач на уроке.
III. Разминка
Мы сегодня будем решать задачи вместе со Смурфиками. (Слайд 4)
Итак! Смурфики вокруг нас! Решение устных логических задач. (Слайд 5)
IV. Решение задач совместно с учащимися на доске
Задача 1 (решается “в отрезках”). (Слайд 6)
В Деревне Смурфов пришло время обеда. Смурфик Повар по особому папиному рецепту испек любимые мини-пиццы смурфиков. Папе и братьям он отнес половину приготовленных мини-пицц и еще одну мини-пиццу. Красотке Смурфетте он преподнес половину остатка и еще одну мини-пиццу, а Ворчуну досталась половина последнего остатка и последняя мини-пицца. Сколько мини-пицц испек Повар по тайному рецепту?
(Поэтапное решение на слайдах 6 – 13 презентации к уроку. Выше было подробно изложено как решать с ребятами эту задачу).
Задача 2 (решается учащимися самостоятельно, первый решивший рисует решение “в отрезках” на доске).
Медведь с базара плюшки нес,
Но, на лесной опушке,
Он половину плюшек съел
И плюс еще полплюшки.
Шел, шел, уселся отдохнуть
И под ку-ку кукушки
Вновь половину плюшек съел
И плюс еще полплюшки.
Стемнело, он ускорил шаг,
Но на крыльце избушки
Он снова пол-остатка съел
И плюс еще полплюшки.
С пустой кошелкою – увы!
Он в дом вошел уныло...
Хочу, чтоб мне сказали вы –
А сколько плюшек было?
Задача 2. Магия чисел (решается по действиям).
Я задумал число, прибавил к нему 5, потом разделил сумму на 3, умножил на 4, отнял 6, разделил на 7 и получил число 2. Какое число я задумал.
Решение.
Решаем задачу с конца:
1) 2 х 7 = 14 – число до деления на 7.
2) (14 + 6) : 4 = 5 – число до умножения на 4.
3) 5 х 3 = 15 – число до деления на 3.
4) 15 – 5 = 10 – искомое число.
Ответ: задумано число 10.
Задача 3 (решается таблицей). (Слайд 14)
Трое мальчиков имеют по некоторому количеству яблок. Первый мальчик дает другим столько яблок, сколько каждый из них имеет. Затем второй мальчик дает двум другим столько яблок, сколько каждый из них теперь имеет; в свою очередь и третий дает каждому из двух других столько, сколько есть у каждого в этот момент. После этого у каждого из мальчиков оказывается по 8 яблок.
Сколько яблок было у каждого мальчика в начале?
Решение.
Решаем задачу с конца с помощью таблицы.
| Номер мальчика | 1 | 2 | 3 |
| Число яблок в конце | 8 | 8 | 8 |
| Число яблок до передачи их третьим мальчиком | 8 : 2 = 4 | 8 : 2 = 4 | 8 + 4 + 4 = 16 |
| Число яблок до передачи их вторым мальчиком | 4 : 2 = 2 | 4 + 2 + 8 = 14 | 16 : 2 = 8 |
| Число яблок первоначально | 2 + 4 + 7 = 13 | 14 : 2 = 7 | 8 : 2 = 4 |
Таким образом, первоначально яблок у первого, второго и третьего мальчиков было соответственно 13, 7 и 4.
V. Самостоятельная работа учащихся по решению задач
Начинаем соревнование!
Я задумал число, умножил его на два, прибавил три и получил 17. Какое число я задумал?
Однажды черт предложил бездельнику заработать.
“Как только ты перейдешь через этот мост, -
сказал он, - твои деньги удвоятся. Можешь
переходить по нему сколько хочешь раз, но после
каждого перехода отдавай мне за это 24 копейки”.
Бездельник согласился и ... после третьего
перехода остался без гроша.
Сколько денег у него было сначала?
Группа туристов отправилась в поход. В первый
день они прошли 1/3 пути, во второй – 1/3 остатка, в
третий – 1/3 нового остатка. В результате им
осталось пройти 32 км.
Сколько километров был маршрут туристов?
Играя в рулетку, Виктор удвоил количество своих
денег, потом потерял 12 рублей. После этого у него
осталось 60 рублей.
С какой суммой он начинал игру?
Над озерами летели гуси. На каждом озере
садилась половина гусей и еще полгуся, остальные
летели дальше. Все сели на семи озерах.
Сколько было гусей?
Домашнее задание: 2-3 задачи с раздаточного материала или из пособия на предложенном сайте, на выбор учителя. (Слайды 16-17)
VI. Итог урока
Учитель еще раз подчеркивает, что для того чтобы успешно решить задачу на части нужно сделать чертеж. Акцентирует внимание учащихся на Памятку (Слайд 15) в раздаточном материале и показанную на слайде.