Мы получили в наследство невыразимо прекрасный
и многообразный сад, но беда в том,
что мы никудышные садовники.
Мы не позаботились о том,
чтобы усвоить простейшие правила садоводства.
Джеральд Даррелл,
«Путь кенгуренка»
Научно-техническая революция… посулив золотые горы
и дав многое из того, чем мы ныне гордимся,
породила иные, ранее неведомые проблемы.
Решить их на путях, проторенных уже,
не представляется возможным.
В.Р. Арсеньев,
«Звери-боги-люди».
В настоящее время термин «экология» стал очень популярным; как правило, его употребляют, говоря о неблагополучном состоянии окружающей нас природной среды. Вместе с тем, его нередко используют в сочетании такими словами, как «общество», «семья», «здоровье», «культура», «образование». Как следствие, закономерен вопрос: «Что же, в конце концов, изучает эта наука?»
Термин «экология» ( от греч.oikos– дом, жилище, родина и logos – слово, учение, наука), предложенный в 1868 г. немецким биологом Эрнстом Геккелем, дословно означает «наука о доме». В самом широком смысле, экология – это комплекс наук об отношениях между организмами и факторами среды их обитания [1, с. 62]. При этом, некоторые науки экологического комплекса классифицируются не по объектам изучения, а по методам исследования, которые в них используются. Одним из таких направлений является «математическая экология».
Математическая экология моделирует экологические процессы, т. е. возможные изменения в природе при изменении экологических факторов [Там же, с. 64]. При этом, небезынтересно отметить, что далеко не всегда возрастающим по сложности системам и объектам соответствуют все более усложняющиеся модели[3]. Весь фокус состоит в том, что математическая модель вовсе не обязана детально описывать изучаемый объект, а может и должна отражать лишь самое важное для изучения.
В свете сказанного рассмотрим несколько примеров.
Пример №1. Алгебра, арифметика и биология[2, с.131-133]. «Однажды в зоопарке я рассматривал зебр, серн, фламинго, нарвалов и бабочек. Всего я насчитал у них тридцать четыре ноги, четырнадцать крыльев, девять хвостов, шесть рогов и восемь ушей, - я хочу сказать, наружных ушей, а не внутренних. Сколько там было зебр? Сколько серн? Сколько фламинго? Сколько нарвалов? Сколько бабочек?»
Решение. Число зебр обозначим буквой x; число серн - y; фламинго - z; нарвалов - u; бабочек - v. Составим и заполним таблицу:
| Ноги | 4x+4y+2z+6v=34 |
Крылья |
2z+4v=14 |
Хвосты |
x+y+z+u=9 |
Рога |
2y+u=6 |
Уши |
2x+2y=8 |
Решив полученную систему уравнений, найдем ответы на поставленные вопросы.
Пример №2. Загадка Каспийского моря[3, с.140, 141]. «Черное и каспийское моря произошли от одного древнего моря, которое было потом разделено Кавказскими горами на две части. Каспийское море замкнутое, Черное вытекает через Босфор и Дарданеллы в Средиземное море. Несмотря на это, Черное море намного соленее Каспийского. Это кажется необъяснимым, но вспомним, что у каспийского моря есть залив Кара-Богаз-Гол. На первый взгляд кажется, что это ничего не меняет, ведь оно по-прежнему остается замкнутым. Однако это не так, поскольку перемешивания вод Каспийского моря и залива не происходит: вода из Каспия все время течет в залив. Может ли это привести к опреснению Каспия?»
Решение. Введем обозначения: Q - общий приток вод в Каспий, I - превышение испарения над дождями в Каспии, I1 - то же в заливе, q- интенсивность перетекания воды из Каспия в Кара-Богаз-Гол, ![]() и
и ![]() 1– скорости изменения объемов воды в Каспии и в заливе, ν - соленость вод рек, притекающих в Каспий, µ - соленость воды Каспия,
1– скорости изменения объемов воды в Каспии и в заливе, ν - соленость вод рек, притекающих в Каспий, µ - соленость воды Каспия, ![]() и
и ![]() 1
1![]() – скорость изменения количеств солей в Каспии и в заливе. Запишем уравнения:
– скорость изменения количеств солей в Каспии и в заливе. Запишем уравнения:
= Q-I-q,
1= q-I1,
= Qν - qµ,
1 = qµ,
где Qν – интенсивность прибытия соли в Каспий, qµ - тоже для залива. Последнее уравнение показывает, что количество солей в заливе неограниченно растет со временем. В геологических масштабах времени можно считать, что![]() =
= ![]() 1= 0, отсюда:
1= 0, отсюда:
Q – I – q = 0,
q- I1 = 0.
Как известно, концентрация солей в заливе давно достигла насыщения, и соли тысячелетиями осаждаются на его дне, образуя громадные залежи. Количество солей в Каспии возрастает до тех пор, пока Qν > qµ. При выполнении условия Qν = qµ рост солености Каспия прекращается, достигнув некоторого значения
µ* = Qν/q = (I+q)ν/= (1+I/q)ν.
Т. к. q = I1, то µ* = (1+I/I1)ν,
где I/I1 – отношение интенсивностей испарения воды в Каспии и в заливе. Грубо приближенно оно равно отношению S/S1 площадей Каспия и залива. С учетом этого:
µ* = (1+I/I1)ν = µ* = (1+S/S1)ν
Т. к. S ≈ 40S1, то µ* ≈ 40ν. Количественные оценки показывают, что это меньше, чем соленость Каспия сегодня. Т. е. залив Кара-Богаз-Гол опресняет Каспийское море, что объясняет его меньшую соленость по сравнению с Черным. В геологических масштабах времени соленость Каспия будет продолжать уменьшаться.
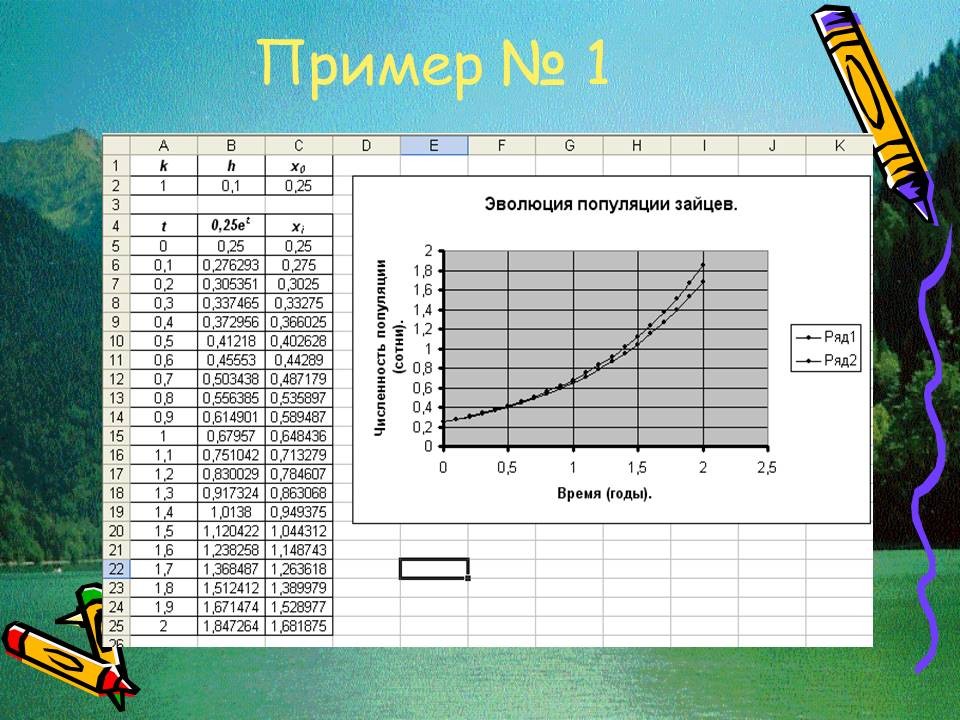
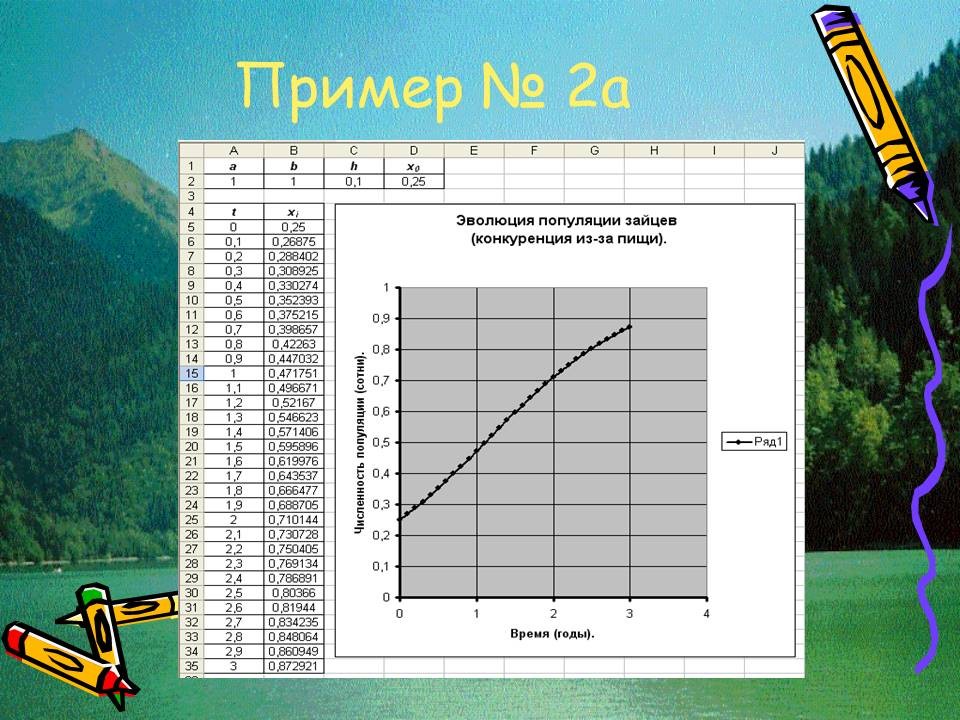
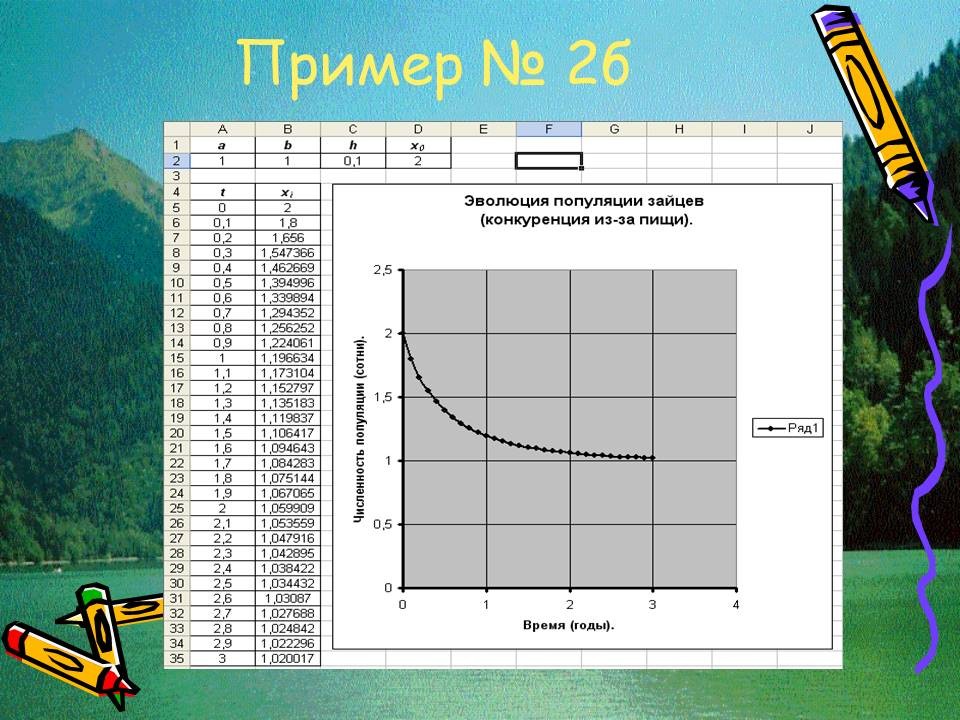
Пример №3. Дифференциальная модель эволюции популяции. Рассмотрим один из важных биологических примеров, основным содержанием которого является исследование развития биосистемы посредством построения динамической модели изменения численности популяции каких-либо живых существ (бактерий, рыб, животных и пр.) с учетом различных факторов. Заметим, что популяции, как правило, существуют не изолированно, а во взаимодействии с другими популяциями. Наиболее важным типом такого взаимодействия является взаимодействие между жертвами и хищниками (например, караси – щуки, зайцы – волки и так далее). При этом отметим, что математические модели «…способствуют более глубокому пониманию закономерностей, раскрывают динамику процесса и связывают воедино разные формы движения материи. В школьном курсе физики мы уже сталкивались с тем, что одно и то же дифференциальное уравнение хорошо описывает и механические колебания маятника, и электромагнитные колебания в контуре. Попробуем эту идею распространить и на другие явления»[4].
Пусть y – количество особей в некоторой популяции хищников, аx – количество их жертв. Тогда скорость изменения количества хищников пропорциональна количеству жертв, а скорость убывания количества жертв пропорциональна количеству хищников, т.е. имеют место дифференциальные уравнения:
Отсюда получим:
Вводя обозначение ω2 = ab, придем к выражению:
.
Последнее, как известно, описывает колебательный процесс с периодом
Таким образом, в данном приближении, изменение численности популяции хищников носит периодический характер. Значения параметров a и b определяются из многолетних наблюдений.
Резюмируем сказанное. Введение в математическую экологию неизбежно требует обращения к физике, химии, математике и информатике. Природные объекты являются высокоорганизованными системами, как на собственном структурном уровне, так и на уровне экосистем. Поэтому, вполне естественно утверждать, что основная цель математической экологии заключается в изучении теории и практики этой организации во всей ее сложности и гибкости, в ее действии и эволюции. И если вводный этап изучения заключается в том, чтобы определить такие факторы, как вес, рост, количество и т. п., то последующие – заинтересоваться соотношениями: больше чем…, более изменчив чем…, больше напоминает…, более чувствителен к…, и т. д., с тем, чтобы, в конце концов, углубиться в раскрытие структуры существенных характеристик избранных объектов. Дальнейшее развитие изложенных идей и принципов отражено в содержании элективного курса «Введение в биометрию» (См. Приложение 1).
Литература
- Габриелян О.С., Дюльдина Э.В., Сладков С.А. Формирование естественно-научной картины мира у старшеклассников при изучении естествознания в соответствии с требованиями ФГОС. Лекции 1-4. – М.: ПУ «Первое сентября», 2012.
- Гершензон М. А. Головоломки профессора Головоломки. – М.: Дет. лит., 1989.
- Неймарк Ю. И. Простые математические модели и их роль в постижении мира.//СОЖ, 1997, №3. С. 139-143.
- Найдин А.А. Математические модели развивают мышление. // Физика (ИД «Первое сентября»), 2008, №12.
- https://fiz.1sept.ru/view_article.php?ID=200801212